GNN(Graph Neural Network)의 정의와 특징 그리고 추천시스템에서의 GNN 계열 모델
- -
들어가기 전에
이제까지 딥 러닝 모델은 CNN(Convolution Neural Network), RNN(Recurrent Neural Network), Transformer 등 다양한 신경망 모델 종류로 발전해 왔다. 그렇지만 복잡한 구조 또는 관계를 지니는 문제를 임베딩하는 데 한계가 있어왔고, 이러한 문제를 해결할 수 있는 모델로서 그래프(Graph)를 사용한 신경망 모델이 제안된다. 이번 글에서는 그래프를 사용한 딥 러닝 모델인 GNN의 정의와 의의에 관해 살펴보고, GNN 모델을 해석하는 관점에서 제시된 여러 종류의 GNN 모델에 관해 살펴보자.
그래프(Graph)의 정의와 사용
그래프는 정보과학을 공부하면 항상 빼 놓을 수 없는 중요한 자료구조이다. 프로그래밍 문제를 푼 사람들이라면 알겠지만 BFS, DFS 등 자주 나오는 알고리즘이 바로 그래프 탐색일 정도로 주어진 문제를 그래프로 해석하여 풀어야 하는 경우가 종종 있다.
이러한 자료구조를 딥 러닝 모델을 사용한 추천시스템에도 적용할 수 있다는 것이 개인적으로 놀라웠는데, 이를 자세히 알기 위해서는 그래프의 정의부터 다시 살펴보는 것이 좋을 것 같아서 그 정의와 그래프를 사용하여 얻을 수 있는 이점에 관해 먼저 살펴보고자 한다.
그래프의 정의
[출처] https://commons.wikimedia.org/wiki/File:Line_graph_construction_1.svg
A graph $G$ consists of two sets, $V$ and $E$, where $V$ is a finite and nonempty set of vertices, and $E$ is a set of pairs of vertices. - Fundamentals of Data Structures, Ellis Horowitz -
그래프는 정점(Node, Vertex)들과 그 노드들을 잇는 간선(Edge)들을 집합으로 모아 구성한 자료 구조이며, 일반적으로 $G = (V, E)$로 정의한다.
이때 $V$는 그래프를 구성하는 정점의 집합, 그리고 $E$는 두 정점을 잇는 간선의 집합이다.
위와 같은 그래프를 정의에 맞게 표현한다면 다음과 같이 정리할 수 있다.
정점은 어떤 한 시스템의 구성 요소를 의미한다고 볼 수 있고, 간선은 이러한 정점들 사이의 관계 또는 상호작용을 표현하는 요소로 볼 수 있다. 그래서 그래프는 정점들과 간선들로 정의되며, 정점의 위치 정보 또는 간선의 순서 등 그 외의 정보는 일반적으로 그래프의 정의에 포함되지 않는다.
그래프의 종류
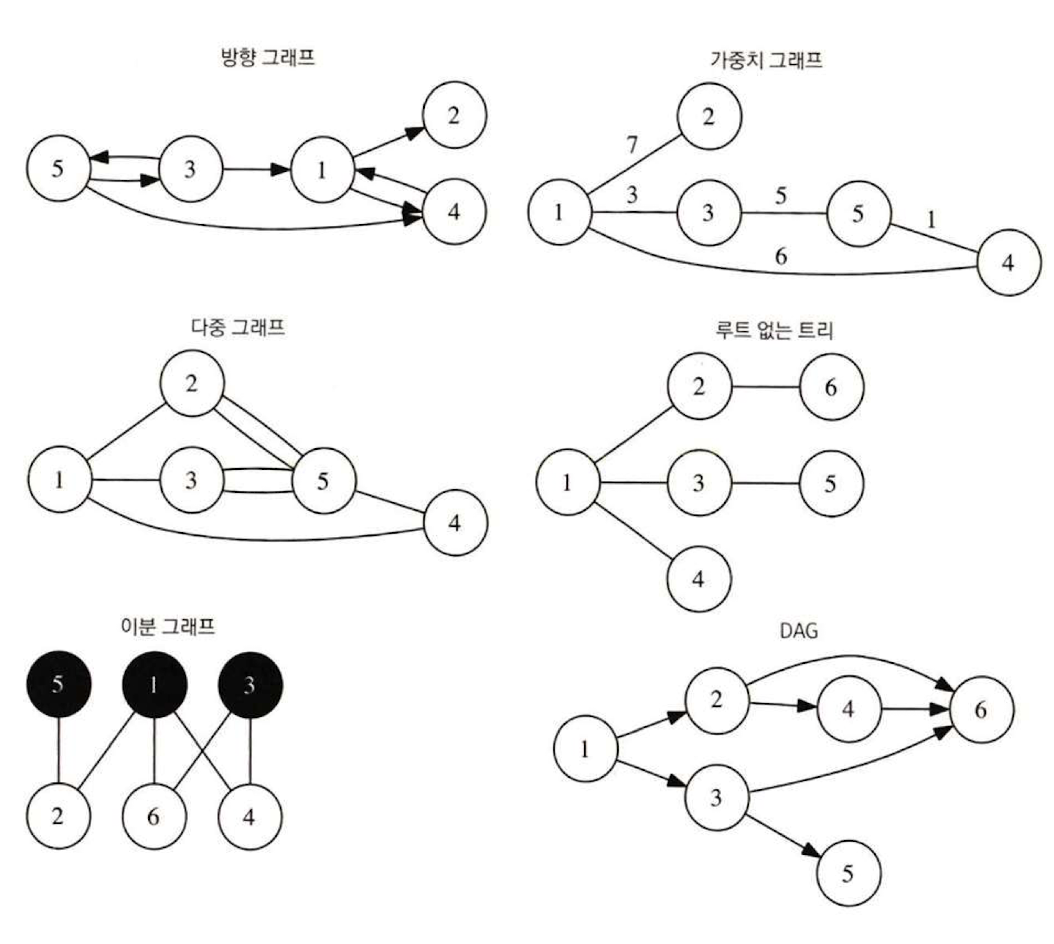
정점들 사이의 관계를 어떻게 정의하는지에 따라 간선의 방향이 존재하는 directed graph(방향 그래프)와 그렇지 않은 undirected graph(무향 그래프)로 나눌 수 있다. 예를 들어, 사람들간의 짝사랑 관계이면 방향 그래프로, 도로의 일방통행이면 무향 그래프로 표현한다.
또한 간선에 가중치가 있느냐와 없느냐에 따라 weighted와 unweighted graph로 나눌 수 있다. 예를 들어, 두 도시 사이의 거리, 두 사람 사이의 호감도, 두 물건 사이의 교환 비율 등 정점 사이의 간선의 정보를 가중치로 부여하는 것이다.
형태에 따라서도 그래프를 simple graph(단순 그래프), multi graph(다중 그래프), bipartite graph(이분 그래프) 그리고 unrooted tree(루트 없는 트리)로 구분할 수 있다.
단순 그래프는 두 정점 사이에 최대 한 개의 간선만 있는 그래프이고, 다중 그래프는 두 정점 사이에 두 개 이상의 간선이 존재할 수 있는 그래프이다.
이분 그래프는 모든 정점이 두 개의 그룹 중 한 그룹에 속하고, 서로 다른 그룹에 속하는 정점끼리만 간선이 존재하는 그래프이다. 주로 이분 매칭으로 풀어야 하는 알고리즘에서 자주 사용한다.
루트 없는 트리는 어떠한 정점이 root 정점인지 지정되지 않은 트리이다.
한 정점에 관해 간선을 한 번만 거쳐서 자기 자신으로 돌아오는 path가 존재하는 cycle이 그래프에서 있거나 없을 수 있는데, 그러한 cycle이 존재하지 않는 그래프를 DAG(Directed Acyclic Graph)라고 한다. 대개 DAG는 위상정렬 시 자주 만나게 되는데, 정점 간의 순서를 정하기 위해 DAG로 구성하여 문제를 푸는 경우가 많아서다.
이 글에서는 GNN에 관해서 집중적으로 설명하는 글이므로 간선의 방향 존재 유무에 따른 그래프 종류와 간선에 가중치 여부와 관련한 그래프 종류, 그리고 이분 그래프만 알고 있어도 좋다.
그래프를 Representation Learning에 사용하는 이유
그러면 그래프를 어떻게 추천 시스템에 활용할 수 있을지 감이 잘 안 잡힐 수 있다. 그전에 그래프가 딥 러닝에서 어떠한 방식으로 사용되는지 이해해 보자.
사실 그래프는 이미 CNN, LSTM, Transformer 등 이미 잘 알려진 Representation Learning 모델과 크게 다르지 않다.
CNN은 Euclidean 공간에서 행과 열로 배열된 픽셀들로 이루어진 이미지에서 특징을 추출한다.
LSTM은 자기 자신으로 돌아오는 recurrent 구조를 통해 input으로 주어지는 어떤 한 시계열 데이터인 sequence의 특징을 추출한다.
Transformer는 self-attention 구조를 통해 어떤 한 부분에서 주의를 기울여야 할 여러 부분을 병렬적으로 함께 처리함으로써 input의 특징을 추출한다.
감이 오겠지만 마찬가지로 GNN에서도 그래프 구조를 통해 시스템에서의 관계 등 다양한 특징을 추출한다.
그래서 학습하고자 하는 데이터를 그래프로 잘 표현할 수 있으면, 우리는 그러한 데이터의 특징을 모델에 학습시킬 수 있다는 것이다.
구체적으로 그래프 구조를 딥 러닝에서 활용하는 이유는 다음과 같다.
추상적 개념을 다루기에 적합하다.
연결되어 있는 데이터를 표현하기에 좋은 특징 덕분에 관계와 상호작용과 같은 추상적인 개념을 다루기에 적합하다. 둘 이상의 상호작용을 테이블과 같이 정형화된 데이터로 표현하면 오히려 복잡해질 수 있지만, 그래프를 사용하면 간단하게 표현할 수 있다.
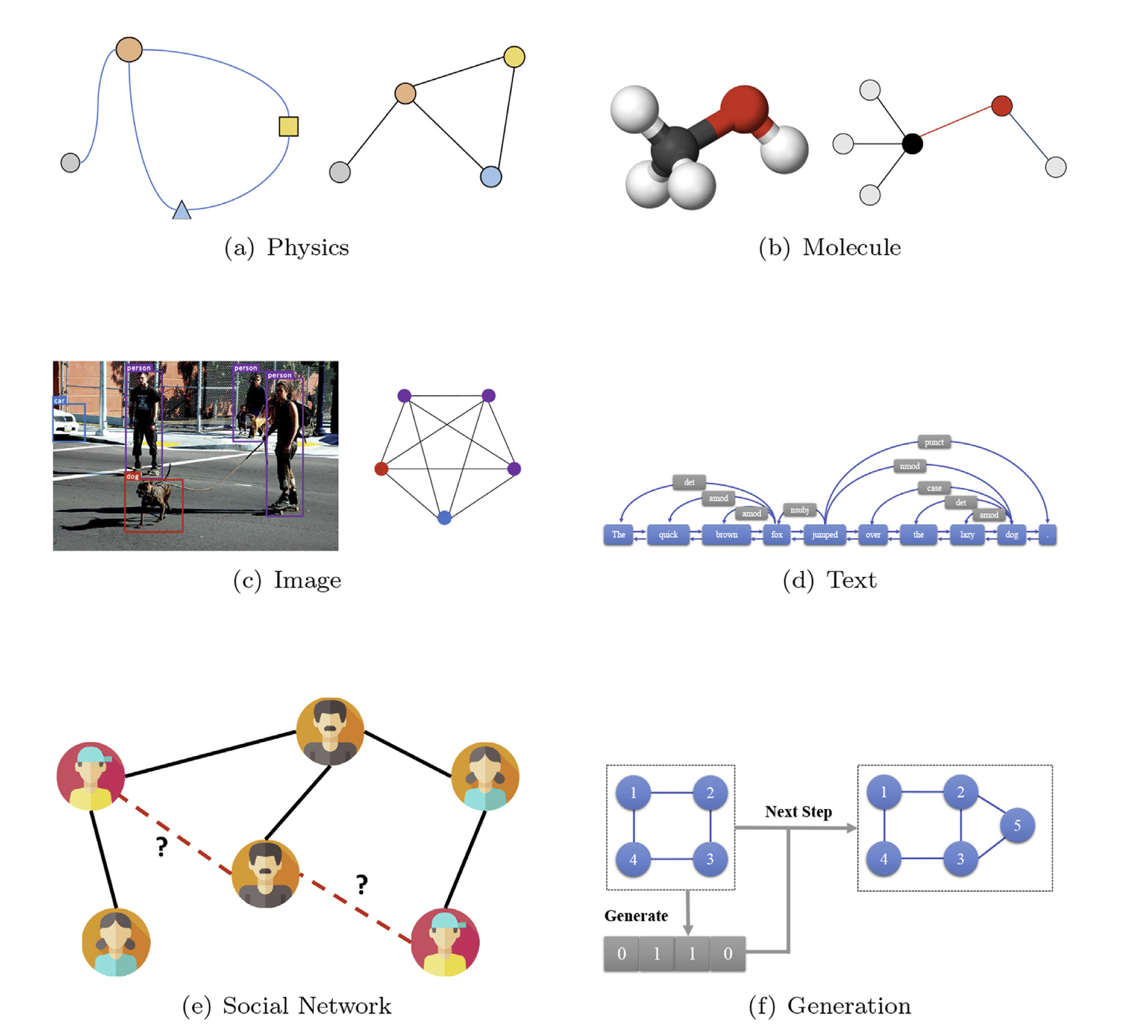
Non-Euclidean Space의 표현과 학습이 가능하다.
흔히 다루는 이미지, 텍스트, 정형 데이터는 격자 형태로 표현할 수 있어서 Euclidean Space에 나타낼 수 있다. 여기서 Euclidean Space는 2차원 평면이나 3차원 공간을 일반화시킨 것이고, 유한한 실수로 표현할 수 있는 공간으로 볼 수 있다.
그러나 그래프를 사용하면 SNS 문자 데이터, 분자(molecule) 데이터 등 일반적으로 Non-Euclidean Space로 표현할 수 없는 데이터를 Non-Euclidean Space에 표현할 수 있게 된다.
[출처] https://arxiv.org/pdf/1812.08434.pdf, Graph neural networks: A review of methods and applications
1. 그래프는 정점과 간선으로 정의되는 자료구조
2. 그래프는 현실 세계의 사물 또는 추상적인 개념 간의 연결 관계를 표현한다.
3. 그래프로 주어진 문제 또는 데이터의 특징을 추출해 보자는 것이 GNN의 아이디어
Graph Neural Network(GNN)
GNN이란?
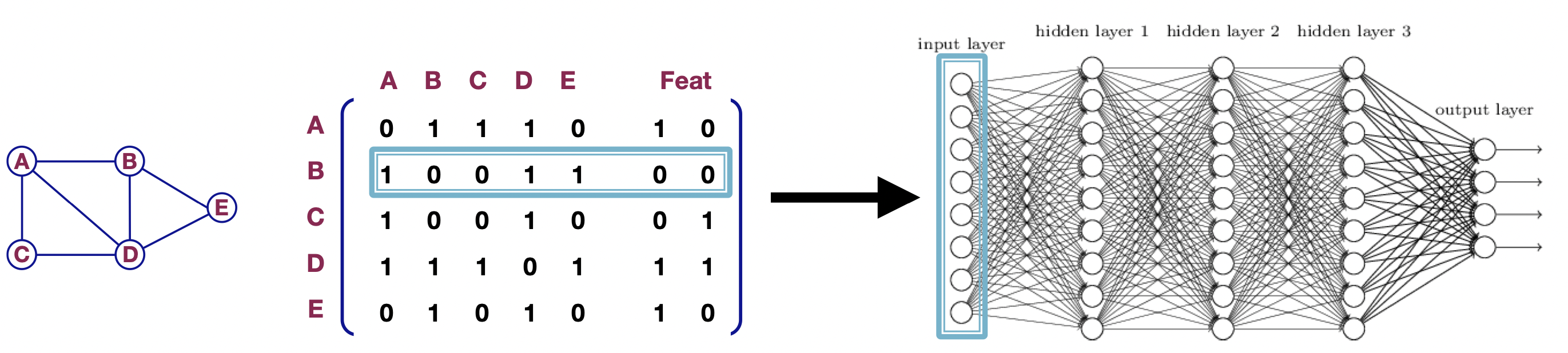
[출처] Jure Leskovec, Stanford CS224W: Machine Learning with Graphs, http://cs224w.stanford.edu
GNN은 그래프 데이터에 적용 가능한 신경망이며, 그래프를 구성하는 각 노드를 잘 표현하는 임베딩을 만든다. 즉, 이웃 노드들 간의 정보를 이용해서 특정 노드를 잘 표현할 수 있는 특징(벡터)을 잘 찾아내는 것이 GNN의 목표이다.
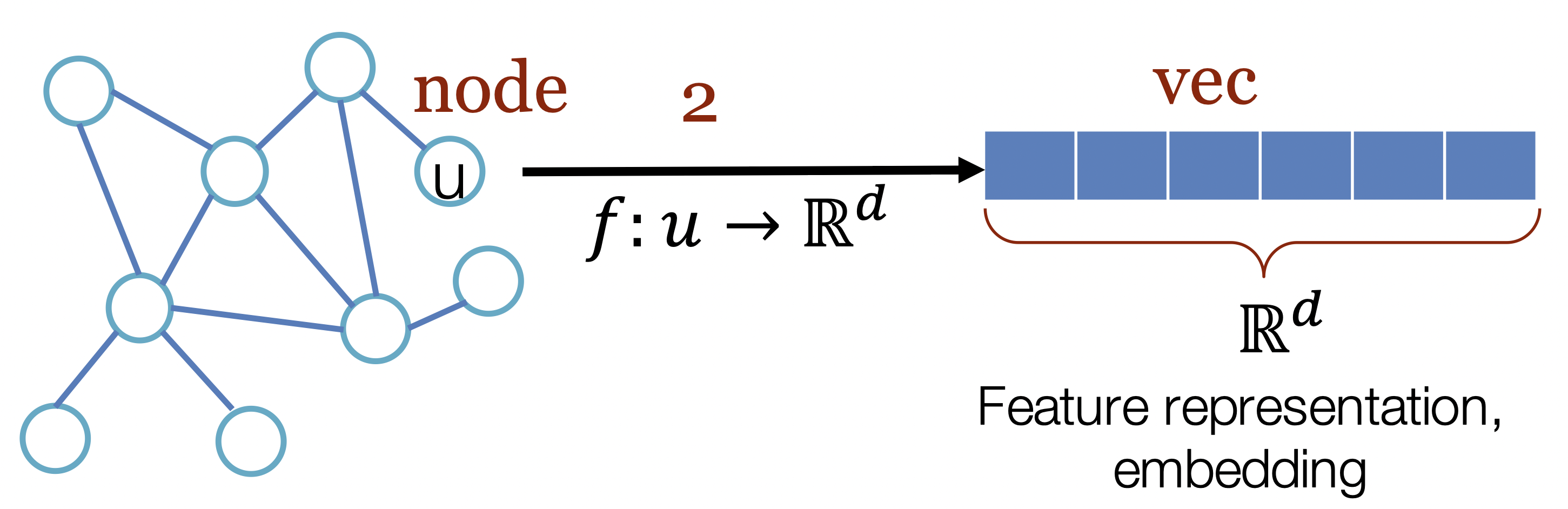
[출처] Representation Learning on Networks, snap.stanford.edu/proj/embeddings-www, WWW 2018
위의 그림에서는 정점 $u$를 잘 표현하는 $d$ 차원의 벡터를 GNN을 통해서 만들 수 있음을 나타낸다.
GNN을 input과 output의 관점에서 볼 때, input으로 주어지는 그래프에서 $x$ 차원의 정점 벡터가 GNN을 거쳐서 $d$ 차원의 특징 벡터인 정점으로 구성되는 그래프를 output으로 내보낸다고 볼 수 있다.
이를 위해 GNN에서는 정점과 간선의 정보와 관계를 표현할 수 있는 수단이 필요한데, 대개 node-feature matrix와 인접 행렬(adjacency matrix)를 사용하여 표현할 수 있다. Node-feature matrix는 정점의 특징에 관한 임베딩 벡터로 이루어진 행렬을 의미하고, 인접 행렬은 정점 간 간선이 어떻게 이어져 있는지 그 관계를 표현하는 행렬이다.
GNN를 학습하는 과정
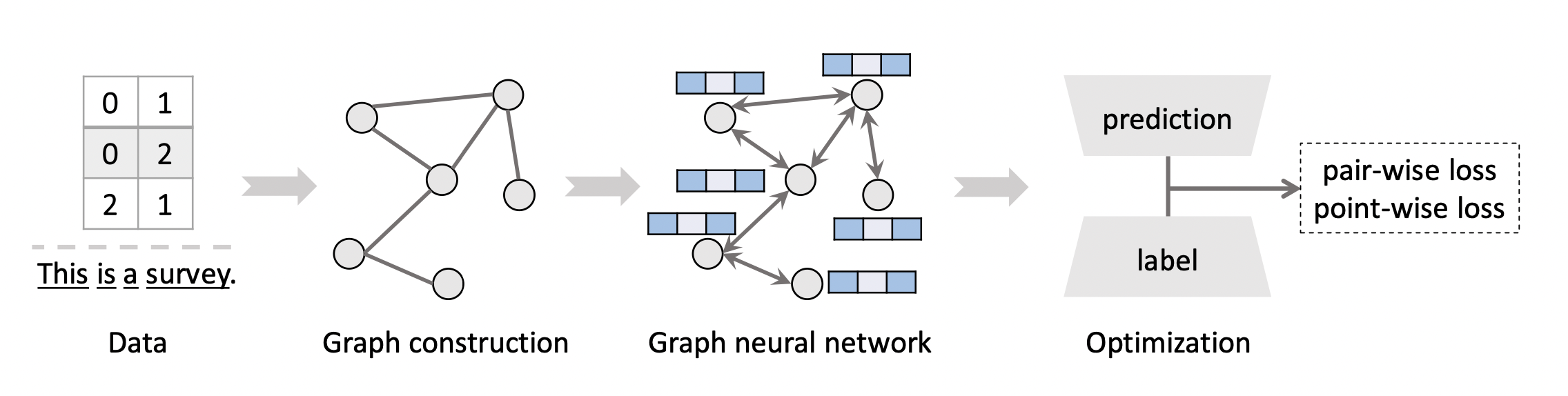
[출처] https://arxiv.org/pdf/2109.12843.pdf, Graph Neural Networks for Recommender Systems: Challenges, Methods, and Directions
GNN도 다른 Neural Network를 학습하는 과정과 크게 다르지 않다.
먼저 주어진 데이터를 인접 행렬 등 그래프로 표현할 수 있는 자료 구조로 변경하는 과정이 필요하다. 예를 들어, 임의의 정점과 연결된 이웃 정점들의 정보를 인접행렬로 표현하는 것이다.
이를 바탕으로 GNN을 학습시키고 나온 예측 값과 GT(Ground Truth)를 비교하여 loss를 계산한다. 이 loss를 최소화하는 방향으로 GNN의 학습 파라미터를 최적화하는 것이 GNN을 학습하는 과정이라고 볼 수 있다.
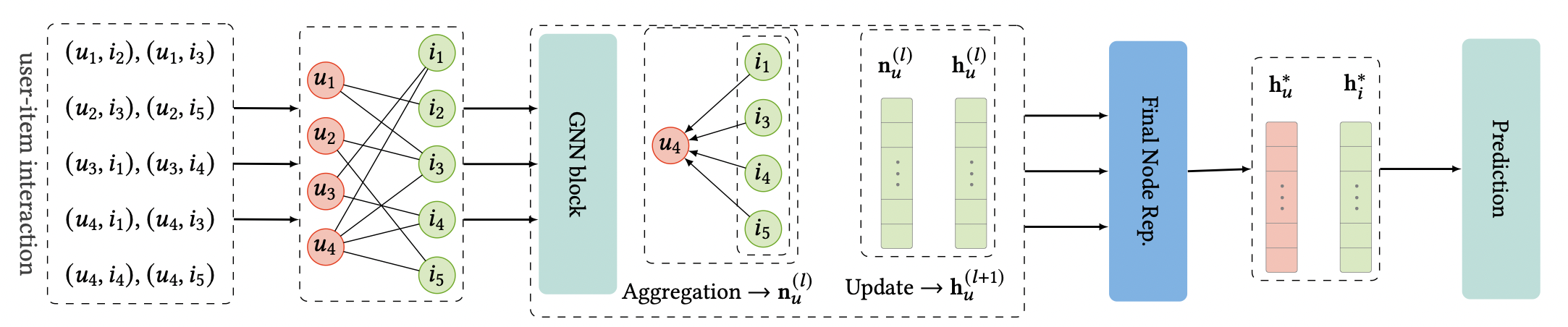
[출처] https://arxiv.org/pdf/2011.02260.pdf, Graph Neural Networks in Recommender Systems: A Survey
유저와 아이템 간의 상호작용을 학습하고 예측하는(한 유저가 어떤 아이템을 좋아하게 될 확률을 학습하고 예측하는 문제인) CF(Collaborative Filtering)에서 GNN을 사용한 전반적인 학습과 예측 과정을 정리하면 위와 같은데, 여기서 task의 종류와 어떤 것을 예측하는지에 따라 예측을 위한 과정이 달라질 수 있다.
위의 그림에서는 GNN 모델이 학습한 유저의 임베딩 벡터와 아이템 임베딩 벡터를 가지고 새로운 유저 또는 아이템 데이터에 관해 예측을 하는 것을 나타내고 있으며, 대표적으로 두 임베딩 벡터를 내적해서 유사도를 구하는 방법이 해당될 것이다.
GNN의 Task 종류
주어진 데이터를 학습한 GNN을 통해 구한 각 정점 $i$의 특징 벡터를 $z_i$라고 하자.
이 $z_i$를 통해 최종적으로 수행하고자 하는 task의 종류는 크게 세 가지가 존재한다.
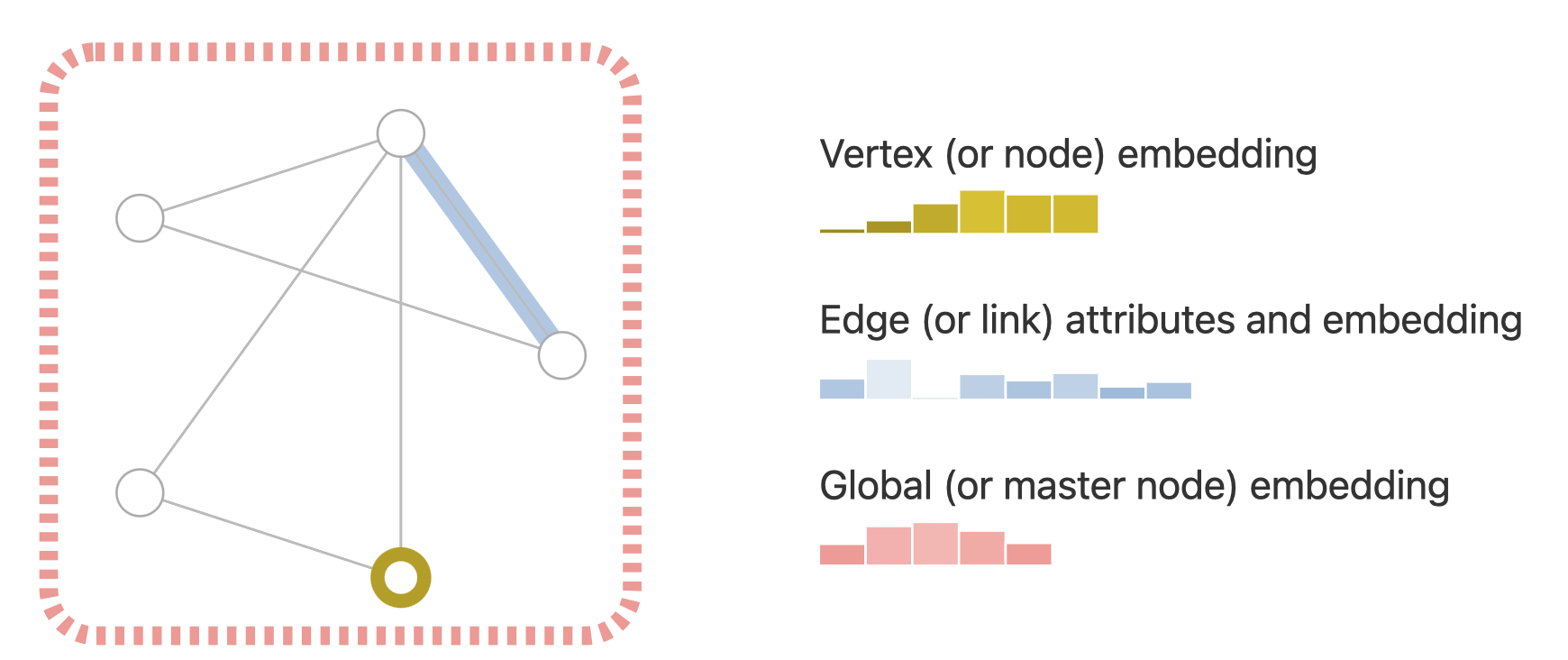
[출처] https://distill.pub/2021/gnn-intro, A Gentle Introduction to Graph Neural Networks
Node Classification
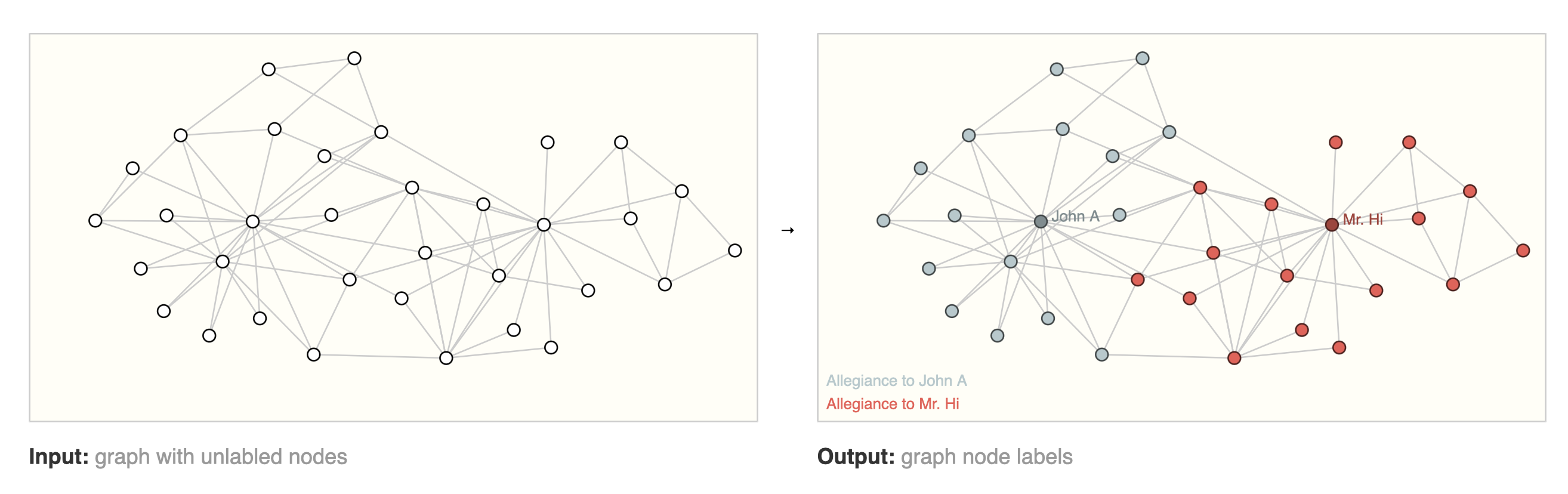
[출처] https://distill.pub/2021/gnn-intro, A Gentle Introduction to Graph Neural Networks
특징 정점 벡터 $z_i$를 통해 정점 $i$를 원하는 레이블로 분류하는 task를 수행할 수 있다. 즉, 임의의 한 정점이 어떠한 레이블에 속하는지 분류하는 작업에서 사용할 수 있는 작업이다.
Graph Classification
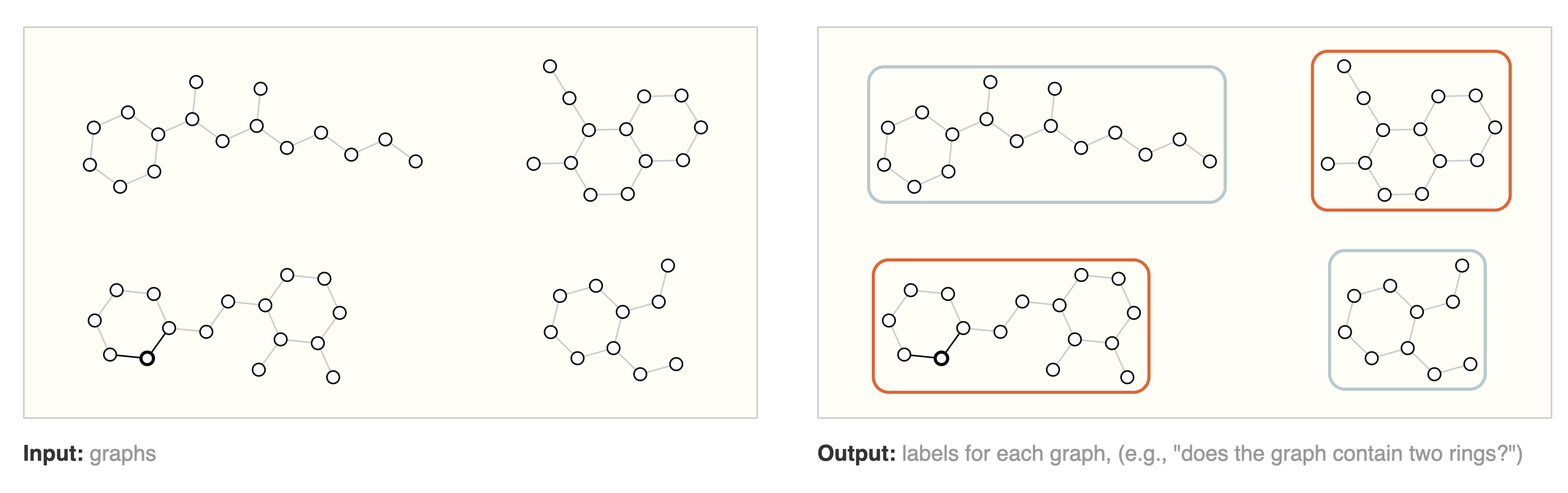
[출처] https://distill.pub/2021/gnn-intro, A Gentle Introduction to Graph Neural Networks
그래프를 구성하는 전체 정점에 대한 특징 벡터 $z_i$를 모두 더하고 softmax를 적용하여 그래프 자체가 어떤 레이블에 속하는지를 분류할 수 있다.
Link Classification
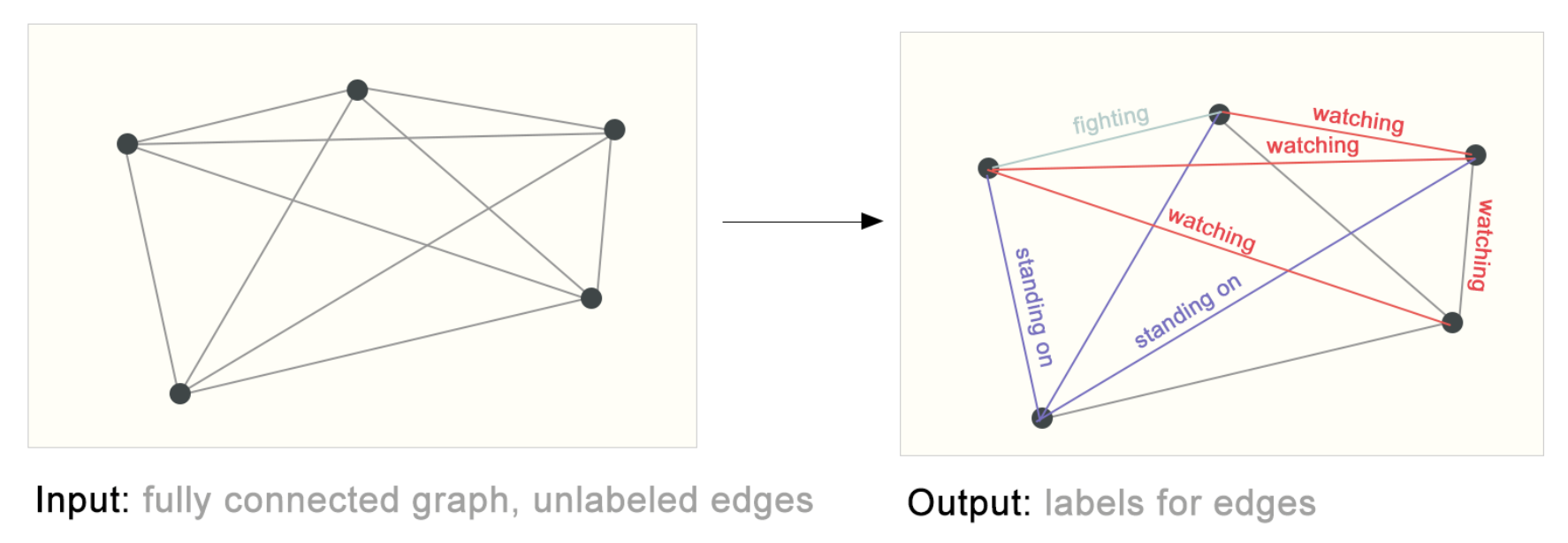
[출처] https://distill.pub/2021/gnn-intro, A Gentle Introduction to Graph Neural Networks
간선으로 연결되지 않은 두 정점 $i$와 $j$이 서로 연결될 수 있는지 없는지를 예측하기 위해 두 정점의 특징 벡터를 내적해볼 수 있다.
이 내적의 결과값이 높으면 서로 상호작용할 확률이 높을 것임을 예측할 수 있다.
데이터를 그래프로 만들어서 각 정점에 관해 특징을 추출할 수 있는 임베딩 벡터를 만드는 게 핵심
이 임베딩 벡터를 어떻게 활용하느냐에 따라 여러 task에 응용하여 사용할 수 있다.
GNN의 방법론
GNN의 방법론에는 크게 spatial 방법과 spectral 방법이 존재하는데, 개인적으로 처음에는 이 둘의 차이를 구분하기 어려웠다. 먼저 Spectral의 방법론을 살펴보고, 이에 대한 한계를 보완할 수 있는 Spatial 방법론을 설명할 것이다.
Spectral 방법론
Spectral 하다는 것은 말 그대로 신호 전처리 분야에서 어떠한 신호를 스펙트럼처럼 분석하는 것을 의미한다.
이 스펙트럼이라는 말이 잘 와닿지 않아 열심히 구글링을 해서 이에 관해 잘 설명한 글을 발견했다.
Spectral Graph Convolution Explained and Implemented Step By Step
As part of the “Tutorial on Graph Neural Networks for Computer Vision and Beyond”
towardsdatascience.com
"Spectral" simply means decomposing a signal/audio/image/graph into a combination (usually, a sum) of simple elements (wavelets, graphlets)
쉽게 이해하자면 영상, 오디오, 이미지, 그래프 등 주어진 어떠한 신호를 frequency domain의 관점에서 단순한 요소의 합으로 분해(decomposition)하는 것을 뜻한다.
이에 관한 대표적인 방법으로 푸리에 변환(Fourier Transform)이 있는데, 이는 어떠한 신호를 $\sin$과 $\cos$ 등 다양한 주파수를 갖는 주기함수인 성분들의 합으로 분해하는 것이다.
하지만 그래프와 GNN에서의 "spectral"는 의미가 달라지는데, 이는 그래프의 라플라시안 행렬(Laplacian matrix)를 고유값 분해(eigen-decomposition)하는 것을 뜻한다.
라플라시안 행렬(Laplacian Matrix)
그러면 라플라시안 행렬($L$)이 또 뭐냐는 질문에 맞닥뜨리는데, 이는 차수 행렬($D$)에서 인접 행렬($A$)를 뺀 것이며 생각보다 정의가 단순하다. 차수 행렬은 각 정점에 관해 몇 개의 간선이 나오거나 들어가는지 그 개수인 차수를 행렬로 표현한 것이고, 인접 행렬은 각 정점이 다른 정점과 직접 간선으로 연결되어 있는지 그 여부를 행렬로 표현한 것이다.
여기서는 편의를 위해 undirected graph로 고려하여 라플라시안 행렬이 대칭(symmetric)이도록 한다.

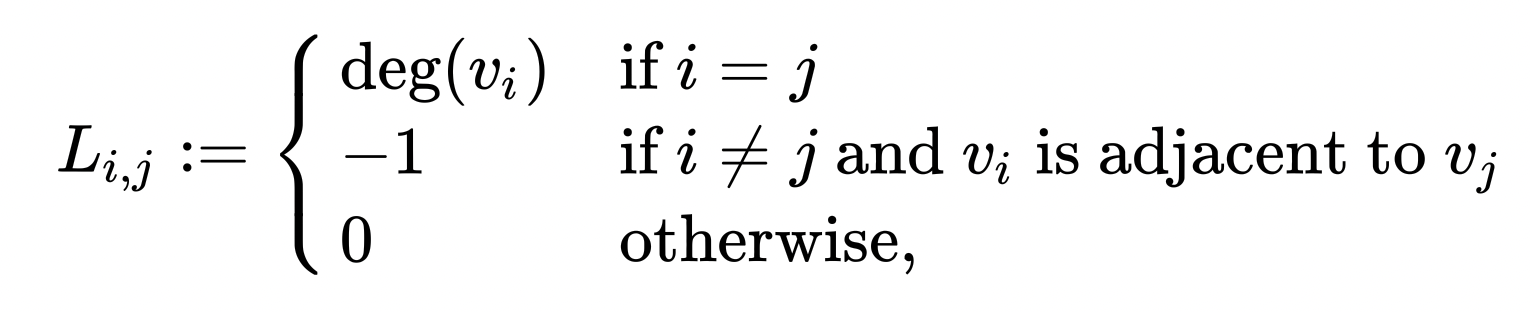
[출처] https://en.wikipedia.org/wiki/Laplacian_matrix
라플라시안 행렬은 차수 행렬에서 인접 행렬을 뺌으로써 인접 행렬을 특수한 방법으로 변환한 것으로 이해할 수 있다. 이러한 라플라시안 행렬은 그래프의 유용한 특성을 찾고자 할 때 많이 사용한다고 알려져 있다.
그런데 이 라플라시안 행렬을 가지고 고유값 분해를 한다는 것이 어떤 내용인지 궁금할 수 있는데, 선형대수학에서 잊힌 내용을 다시 복습하는 겸 고유값과 고유 벡터부터 정리해 보았다.
고유값과 고유 벡터
교유값(eigenvalue)와 고유벡터(eigenvector)에 관하여 아래 글에서 간략히 정리한 적이 있다.
[빠르게 정리하는 선형대수] Eigenvalue와 Eigenvector
Eigenvalue와 Eigenvector 선형대수학을 공부할 때 가장 중요하면서도 기초가 되는 내용 중 하나이며, 실제로 AI에서 자주 등장하는 개념이기도 하다. 기본이지만 그만큼 여러 번 짚고 가도 부족할 정
glanceyes.com
정방행렬 $A$에 관하여 $A \mathbf{x} = \lambda \mathbf{x}$를 만족하는 0이 아닌 열벡터 $\mathbf{x}$가 존재할 때, 상수 $\lambda$를 고유값, $\mathbf{x}$를 고유 벡터라고 한다.
즉, 벡터 $\mathbf{x}$에 관하여 선형 변환 $A$를 했을 때, 벡터의 크기만 변하고 방향이 변하지 않는지를 구한다. 그래서 고유값과 고유 벡터를 구할 수 있다는 것을 보임으로써 굳이 선형 변환을 하지 않고 벡터의 scale만 변화시킬 수 있음을 알 수 있다.
우리가 어떠한 선형 변환 $A$를 임의의 벡터 $x$에 적용한다고 하더라도 그 선형 변환은 단순히 원래 벡터 $x$에 실수배 한 것과 다르지 않은 것이므로 $x$는 그래프의 중요한 정보를 갖고 있다고 보는 아이디어에서 출발한다고 볼 수 있다.
고유값 분해
고유값 분해는 말 그대로 행렬 $A$를 고유값과 고유 벡터로 분해하는 것을 의미한다.
예를 들어, 행렬 $A$의 고유값을 $\lambda_i$, 고유 벡터를 $v_i$라고 하면 다음과 같이 정리할 수 있다.
이 고유값과 고유 벡터를 묶어서 다음과 같이 고유값 행렬과 고유 벡터 행렬을 정의할 수 있다.
고유벡터행렬 $V$는 고유 벡터를 열벡터로 옆으로 쌓아서 만든 행렬, 고윳값 행렬 $\Lambda$는 고유값을 대각성분으로 가지는 대각행렬이다.
이를 통해 행렬 $A$와 고유 벡터 행렬 $V$의 곱을 고유 벡터행렬 $V$와 고유값 행렬 $\Lambda$의 곱으로 나타낼 수 있다.
고유 벡터 행렬 $V$의 역행렬이 존재하면 이를 우변으로 정리하여 다음과 같이 표현할 수 있는데, 이를 고유값 분해라고 한다.
그러면 이 고유값 분해가 GNN과 어떤 관계가 있는지 궁금해질 수 있다. 정리하면 고유값 분해는 그래프를 구성하는 단위 직교 요소(elementary orthogonal component)를 찾을 수 있는 방법이며, 전반적인 그래프의 핵심적이면서도 원하는 정보(주파수)만을 뽑아내 좀 더 유의미한 정보를 얻기 위한 과정이다.
이때 그래프의 라플라시안 행렬의 단위 직교 eigenvector는 그래프의 topology에 관한 정보를 갖게 된다. Eigenvalue가 작은 eigenvector는 그래프의 local 구조를, eigenvalue가 큰 eigenvector는 그래프의 global 구조에 관한 정보를 갖는다. 여기서 potential(signal)이 주어질 경우 이를 앞에서 말한 eigenvector가 이루는 space로 투영해서 eigenvector들에 관한 선형결합으로 나타낼 수 있다. 이를 통해 해당 signal이 어떻게 흩어지는지(diffusion)에 관한 정보를 파악하는 게 가능하다. 여기서 signal이라는 말이 자주 언급되는데, 이는 어떤 한 정점이 갖고 있는 특징이라고 이해할 수 있다.
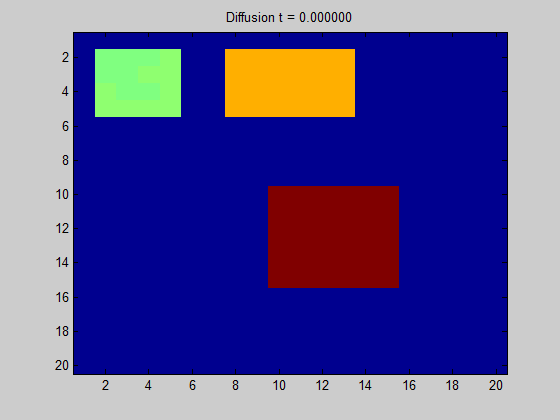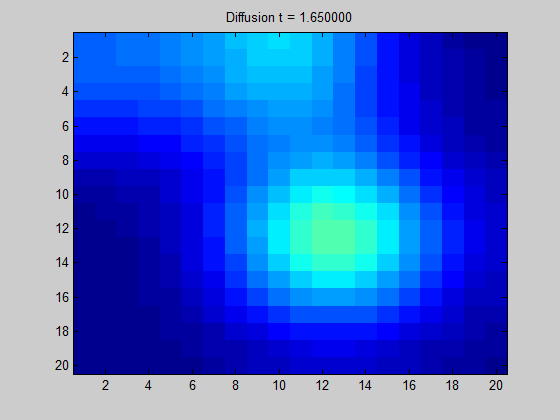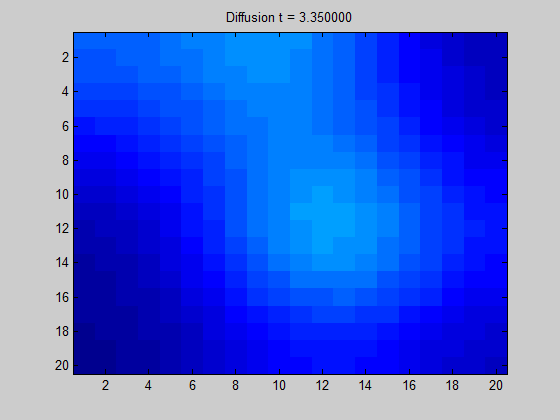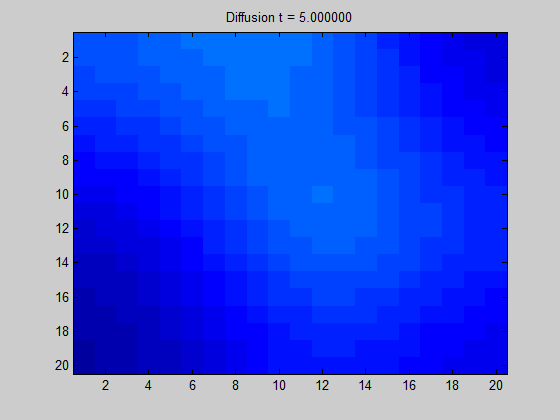
[출처] https://towardsdatascience.com/spectral-graph-convolution-explained-and-implemented-step-by-step-2e495b57f801, Boris Knyazev
위의 GIF 이미지를 어떤 한 그래프로 고려하면, 어떤 픽셀(정점)에서 signal이 주어질 때 이 signal이 어떻게 흩어지는지를 볼 수 있다. 인접한 픽셀과의 색상 변화가 두드러지게 나타나지 않는다면 signal이 주변 픽셀로 부드럽게 흩어짐을 의미한다.
즉, Spectral 방법론은 그래프의 정점 간 연결성(구조)을 보존하면서 그래프의 위상(topology)를 파악하는 동시에 그래프에서 signal이 어떻게 흩어지는지를 이해하여 전반적으로 유의미한 특성을 찾아내고자 그래프의 라플라시안 행렬을 찾아 이를 고유값 분해한다.
이를 통해 찾아낸 고유 벡터를 이용하여 Graph Fourier Transform을 정의한다. Graph Fourier Transform은 라플라시안 행렬 $L$의 eigen space에 존재하는 임의의 행렬 $\mathbf{x}$가 있을 때, 이를 직교하는 영역인 $L$의 orthonormal eigenvector space로 투영(projection)시켜서 그래프의 signal이 어떻게 흩어지는지를 얻는다. 이 space에서의 eigenvector는 그래프의 위상 정보를 담고 있고, 작은 eigenvalue 값을 지니는 eigenvector는 그래프의 local 정보를, 큰 eigenvalue 값을 지니는 eigenvector는 그래프의 global 정보를 갖는다. 또한 그 공간에서 signal의 변화를 의미하는 벡터는 이러한 eigenvector의 선형결합으로 표현될 수 있다. 이는 앞에서 말한 푸리에 변환(Fourier Transform)과 유사한데, 그래프를 나타내는 어떤 한 signal이 주어질 때 이를 표현 가능한 어떤 함수들의 합으로 표현함으로써 그래프의 정보를 구성하는 latent 요소를 파악하는 것과 유사하기 때문이다.
Spatial 방법론
후술하겠지만 마치 CNN에서처럼 target 정점의 주변 이웃 정점의 정보를 가져와서 aggregation하여 target 정점의 정보로 업데이트하는 것이 spatial 방법이라고 볼 수 있으며, 대표적으로 GCN이 spatial 방법론의 특성을 가진다고 볼 수 있다. (그렇다고 GCN이 완전한 spatial 방법론에 속한다고 보기는 어렵다. 이에 관한 이유는 후술할 것이다.) GCN을 자세히 설명하면서 spatial 방법론을 이야기하는 것이 더 바람직할 것 같아서 먼저 GCN부터 살펴보도록 하자.
Spectral 방법론: 그래프의 라플라시안 행렬을 찾아 고유값 분해하여 그래프의 latent 정보를 파악
Spatial 방법론: 인접한 정점의 정보를 고려하여 현재 정점의 정보를 업데이트하여 정점의 임베딩 학습
Graph Convolution Network(GCN)
GCN이란?
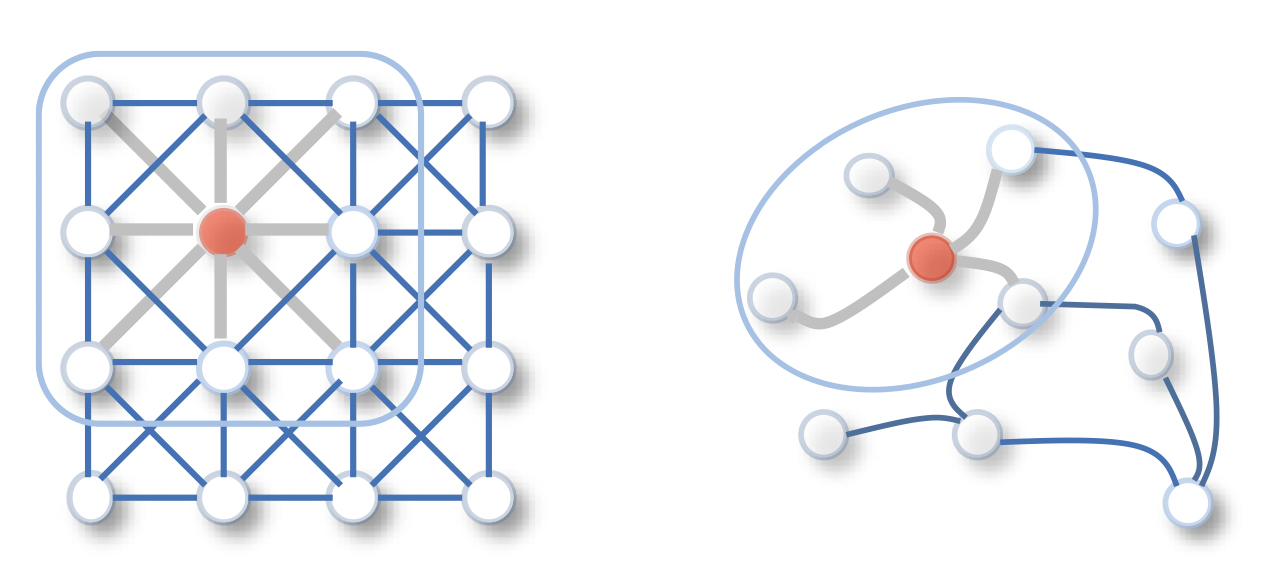
[출처] https://arxiv.org/pdf/1901.00596.pdf, A Comprehensive Survey on Graph Neural Networks
GCN은 용어 그대로 그래프에서 CNN에서처럼 커널 또는 필터를 이용하여 convolution 연산을 수행하면서 그래프의 내재된 정보를 학습하는 모델이다. 이미지를 인접한 픽셀끼리 연결된 그래프라고 생각하면, CNN에서 커널을 이동해 가며 학습하는 것도 graph convolution의 일종으로 볼 수 있다.
그런데 CNN에서 사용하는 이미지 데이터는 픽셀의 위치와 다른 픽셀 간의 거리가 중요해서 locality를 학습하지만, 그래프는 non-euclidean 공간에 존재하므로 거리가 아닌 관계 그 자체가 중요하며, 정점 간의 연결 강도가 어느 정도인지를 학습하는 것이 중요하다. 즉, 서로 중요하게 학습하는 대상은 다르지만 CNN과 GCN 모두 convolution을 수행하는 방식은 유사하다고 볼 수 있다.
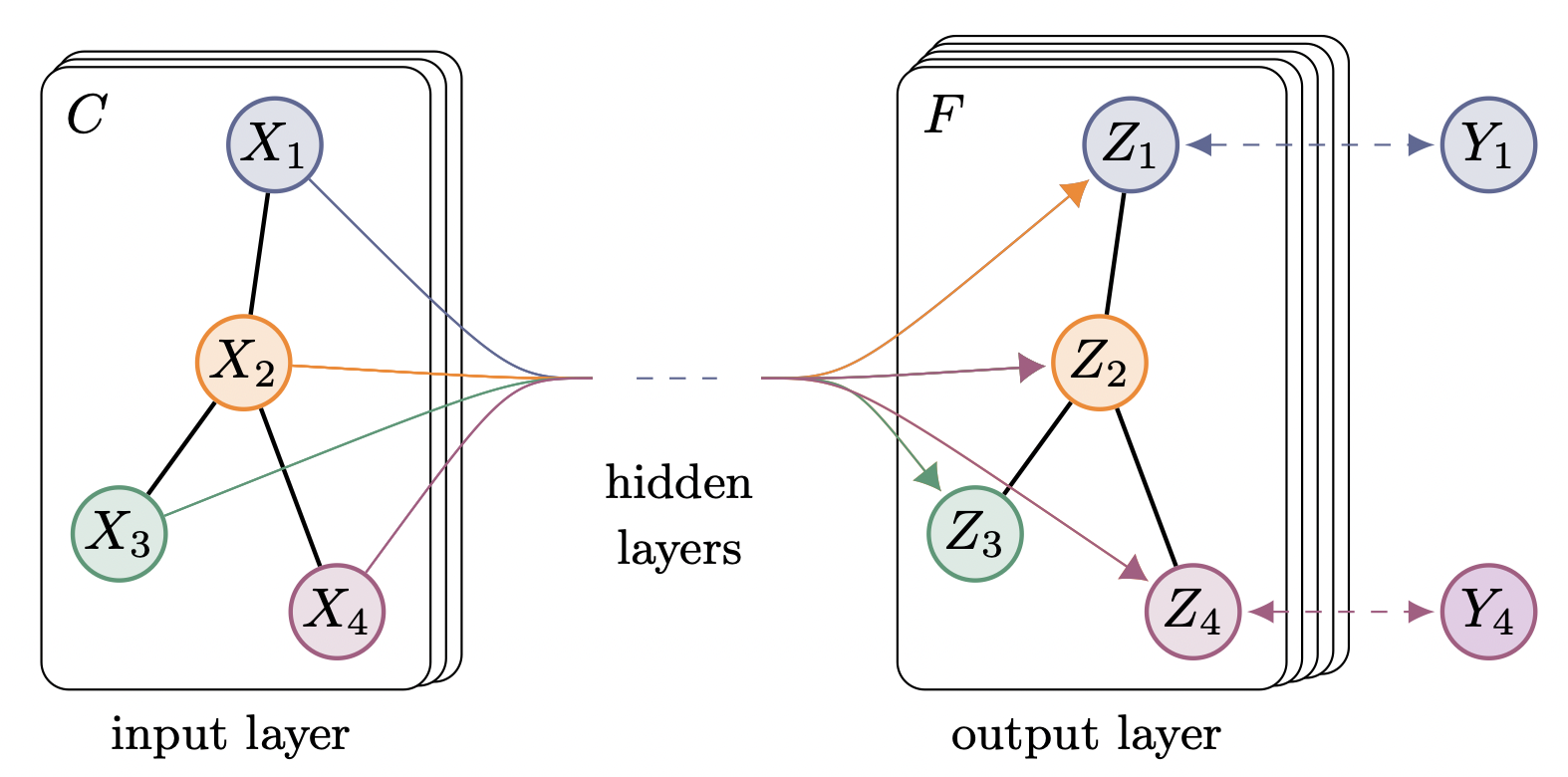
[출처] https://arxiv.org/pdf/1609.02907.pdf, Semi-Supervised Classification with Graph Convolutional Networks
앞서 말했지만 GCN은 완전한 spatial GCN은 아니다. 정확하게 GCN은 spectral 방법론에서 spatial 방법론으로 연결해주는 방법에 속한다고 볼 수 있는데, Spatial domain의 convolution 연산이 Fourier domain에서의 곱과 같다는 성질을 이용하여 인접 정점으로부터 convolution 연산을 사용하기 때문이다.
Spatial 방법론 관점에서 GCN은 neighborhood aggregation을 수행하는데, 이는 어떤 target 정점의 주변 이웃 정점의 정보를 가지고 자기 자신의 정보를 업데이트하는 것을 뜻한다. 이때 주변의 각 이웃 정점으로부터 target 정점에 얼만큼 정보를 전달시킬지를 message라고 한다. 이처럼 graph convolution은 target 정점과 연결된 이웃들의 정보를 가중 평균하거나 단순 합을 한다고 볼 수 있다.
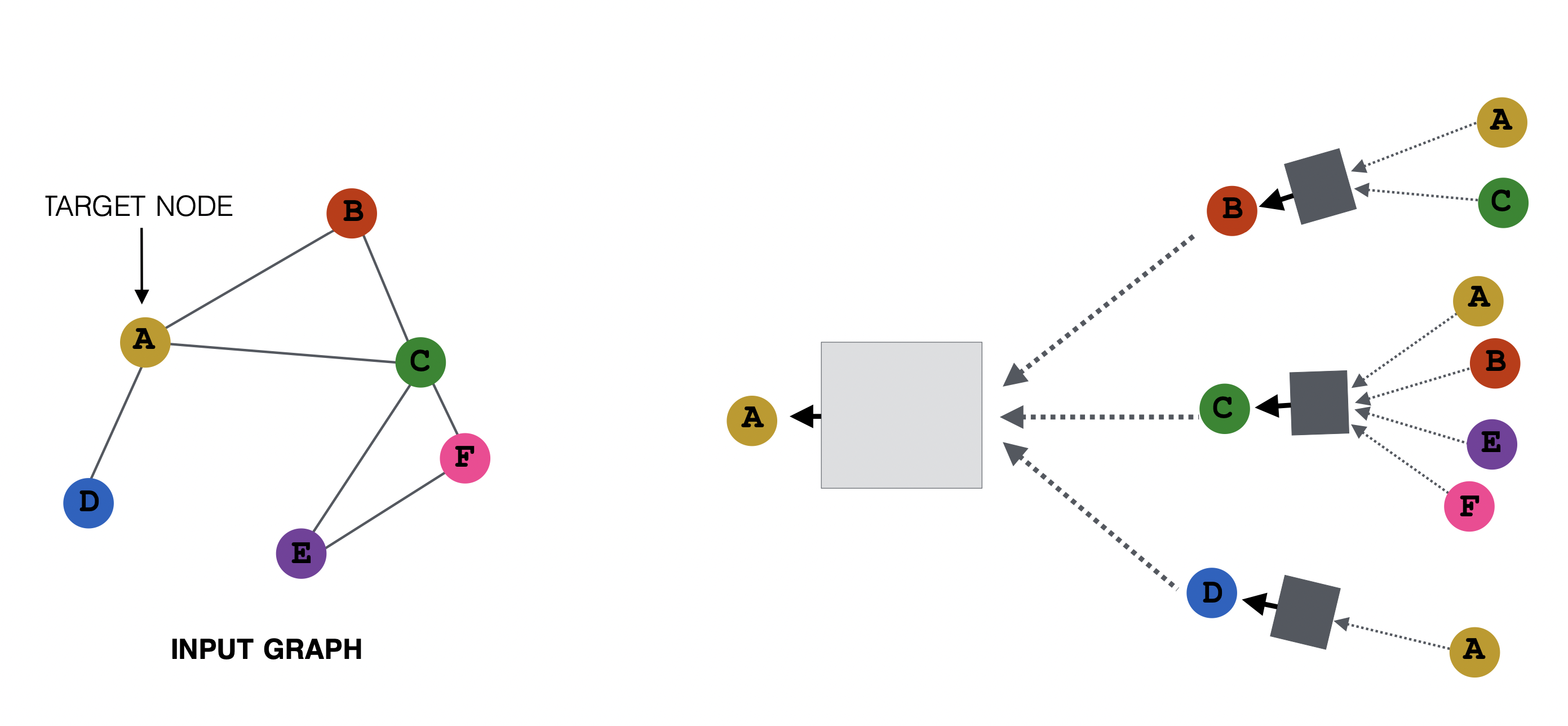
[출처] https://web.stanford.edu/class/cs224w/slides/06-GNN1.pdf, CS224W: Machine Learning with Graphs
앞에서 말한 node-feature matrix을 가지고 말하면, GCN은 node-feature matrix와 adjacency matrix를 사용하여 주변 이웃의 벡터 정보를 aggregate하고 이를 target의 임베딩 벡터 또는 hidden representation에 업데이트하는 것으로 해석할 수 있다.
위의 예시처럼 neighborhood aggregation을 적용한다고 가정하면, 다음과 같이 식을 작성할 수 있다.
$l$은 몇 번째 레이어에 해당되는지를 의미하고, $N(i)$는 정점 $i$의 이웃 정점, $A$는 인접 행렬, $W$는 임베딩 행렬에 곱해서 feature transformation을 하기 위한 가중치이자 학습 파라미터, $H_i$는 각 정점의 임베딩 행렬, $b$는 bias이다.
위의 예시에서는 Target 정점인 $A$의 주변 노드에 대한 정보를 학습하는 것이며, 이때 학습 가능한 파라미터인 $W$는 공유된다. 또 이 예시에서는 주변 이웃 정점의 정보를 aggregation할 때 파라미터 $W$를 가중치로 하여 가중 합을 하는 방식을 사용하지만, 이를 가중 평균으로 가져올 수도 있다.
GCN에서의 파라미터
GCN의 목적은 target의 주변 인접 정점의 정보를 통해 target 자신의 정보를 hidden representation으로 만들 수 있는 최적의 필터인 $W$를 찾는 것이다. 이 필터 $W$는 가중치이자 학습 가능한 파라미터이며, 다른 정점의 hidden representation을 사용할 때도 공유(sharing)된다.
또한 $H$의 차원에 의존하므로 $W$의 차원은 그래프의 전체 정점의 수인 $n$과 관계가 없으며, 정점의 순서와도 무관(order invariant)하다.
GCN과 인접행렬
그러나 위에서의 인접행렬 $A$는 이웃 정점과의 연결만 표현하고 정작 자기 자신인 target 정점 자체의 feature는 고려하지 못한다. 그래서 자기 자신으로 돌아오는 self loop이 있다고 가정하여 새로운 인접행렬 $\tilde{A}$를 사용하는데, 이는 $\tilde{A} = A + I$로 볼 수 있다.
이처럼 자기 자신의 정보를 주변 이웃에서 온 정보와 합치는 과정을 combine이라고 부르며, 주로 인접 행렬에 차원이 같은 단위 행렬을 곱하는 방법으로 수행한다. 물론 자기 자신의 정보에 관해 새로운 파라미터를 가지고 feature transformation하여 더할 수도 있지만, 이는 학습할 파라미터가 늘어나서 모델의 복잡도를 높이게 되므로 self loop를 추가하여 고려하는 인접행렬을 쓰는 방법이 더 효율적이다.
GCN에서 인접행렬 $A$는 degree 관점에서 정규화되어 있지 않으므로 연산 시 feature 행렬의 크기가 불안정해질 수 있다. 그래서 각 정점의 degree로 정규화해주는데, 이를 symmetric renormalization trick이라고 한다.
이처럼 GCN을 학습할 때 인접행렬 $A$가 사용되면서 그래프의 구조적인 전체 정보를 반영하는데, 이 점이 spatial한 GCN에 spectral 방법이 반영되어 있다고 해석하는 이유 중 하나이다.
GCN의 특징
Local Connectivity
주어진 데이터와 물리적으로 가까이 있는 데이터를 가지고 convolution 연산을 수행하는 것이며, 그래프에서는 한 정점에 관해 인접해 있는 이웃한 정점 데이터를 가지고 convolution 연산을 수행하는 것이다.
Shared Weights
CNN에서 커널(kernel) 또는 필터(filter)를 이동해 가면서 커널의 weight을 공유하여 convolution을 수행했는데, GNN의 그래프에서도 마찬가지로 앞서 말한 바처럼 동일한 파라미터인 weight($W$)을 가지고 convolution 연산을 수행하게 된다.
Multi Layer
Convolution Layer를 둘 이상 쌓게 되면 좀 더 넓은 영역을 필터에 포함시켜서 convolution을 수행할 수 있다. 이를 흔히 receptive field을 크게 한다고 말하는데, 그래프에서도 마찬가지로 레이어를 추가하여 바로 인접한 정점 외의 좀 더 멀리 있는 정점도 convolution을 수행할 수 있다.
Transductive Learning
GCN은 transductive learning에 속하며, transductive learning을 설명하기 전에 이와 대조되는 inductive learning을 먼저 알아보자.
Inductive learning은 지도학습으로 볼 수 있으며, 모델을 학습할 때 미리 label이 주어지고 이에 대한 예측 결과를 가지고 모델이 학습을 진행한다. 즉, label이 있는 데이터로 모델의 파라미터를 학습하며, 모델을 test하거나 inference 할 때는 이미 학습이 완료된 모델을 가지고 학습을 더 진행하지 않고 예측을 한다.
반면에 transductive learning은 test하거나 inference 할 때도 모델 학습을 진행하며, 이를 통해 나온 결과로 특정 input에 관해 예측을 수행한다. 그래서 GCN에서 새로운 정점이 생기거나 그래프 구조가 변하면 전체 그래프와의 연결성을 다시 고려해야 하므로 다시 학습을 진행해서 예측을 한다.
정리하자면, 테스트나 추론 전에 미리 명시적인 모델의 파라미터를 학습하지 않는다는 게 transductive과 inductive learning의 차이로 볼 수 있다.
GCN의 Receptive Field
CNN에서 여러 번 convolution 연산을 수행하면 receptive field가 넓어지는 것과 같이 GCN의 레이어를 여러 개 쌓으면 바로 인접한 이웃 정점을 넘어서 그 이웃 정점의 주변 정보도 같이 가져올 수 있다.
import torch.nn as nn
class GCN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = GCNConv(dataset.num_node_features, 16)
self.conv2 = GCNConv(16, dataset.num_classes)
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training=self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
일반적으로 GNN에서는 바로 인접한 이웃 뿐만이 아니라 몇 번 건너게 되는 이웃까지 볼 것인지를 hop이라고 칭한다.
Over Smoothing
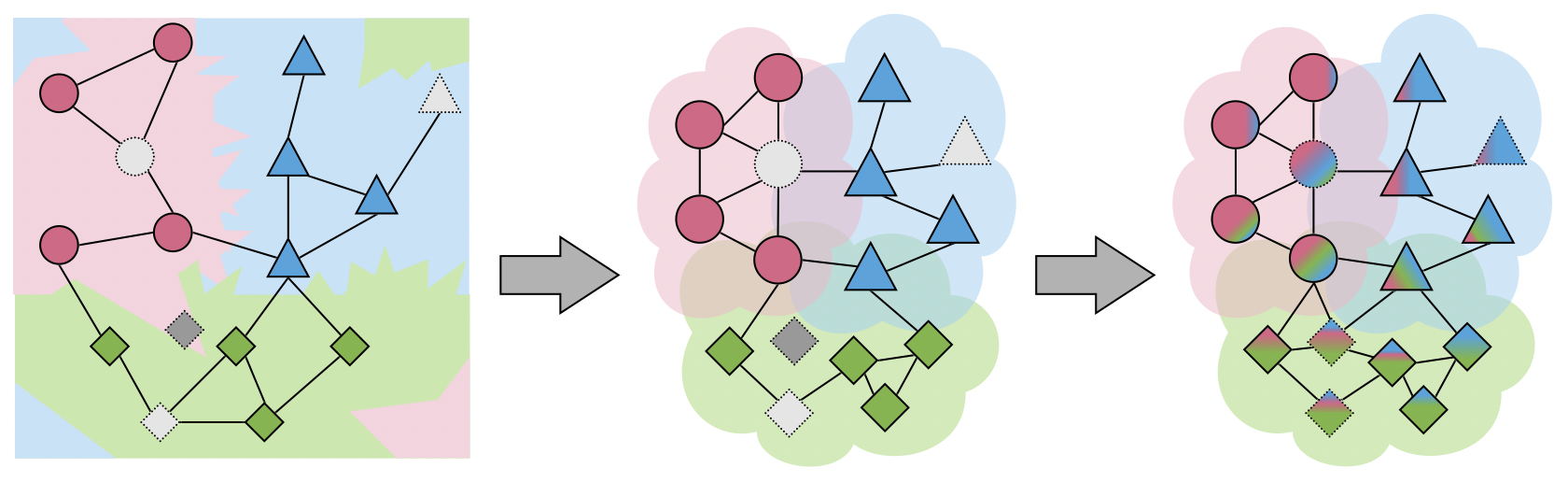
[출처] https://www.ecva.net/papers/eccv_2020/papers_ECCV/papers/123710120.pdf, Embedding Propagation: Smoother Manifold for Few-Shot Classification
GCN 또는 GNN에서 여러 번 건넌 이웃까지 target 정점의 정보로 반영하게 되면서 정점의 임베딩 벡터가 결국 국소 지역의 정보의 평균으로 될 가능성이 있다. 이는 결과적으로 어떤 한 정점이 주변 정점에 의해 기존에 갖고 있던 임베딩 벡터가 희석되어 정점 간의 임베딩 벡터가 서로 비슷해지는 결과를 낳게 된다.
그래서 주변의 많은 정보를 반영하는 게 항상 좋은 게 아니며, 일반적으로 데이터셋에 따라서 GCN에서 레이어 수가 4를 넘으면 성능이 떨어지는 경우가 있다고 알려져 있다.
이러한 over-smoothing을 예방하는 방법으로는 정점 또는 간선을 dropout하는 방법이 있고, 레이어에 따라서 간선을 랜덤하게 dropout하여 각 레이어마다 다른 subgraph를 만드는 random walk 방법도 존재한다. 희석된 모든 정점 임베딩 벡터를 영점으로 옮겨서(centering) 이를 다시 rescaling하는 pair norm 방식을 사용할 수도 있다.
GCN의 핵심
1.CNN처럼 인접한 정점의 정보를 aggregation하여 정점의 임베딩 벡터를 업데이트
2. 인접 행렬을 사용하므로 Spectral 방법과 Spatial 방법을 연결해 주는 방법론
Graph Attention Network(GAT)
GAT란?
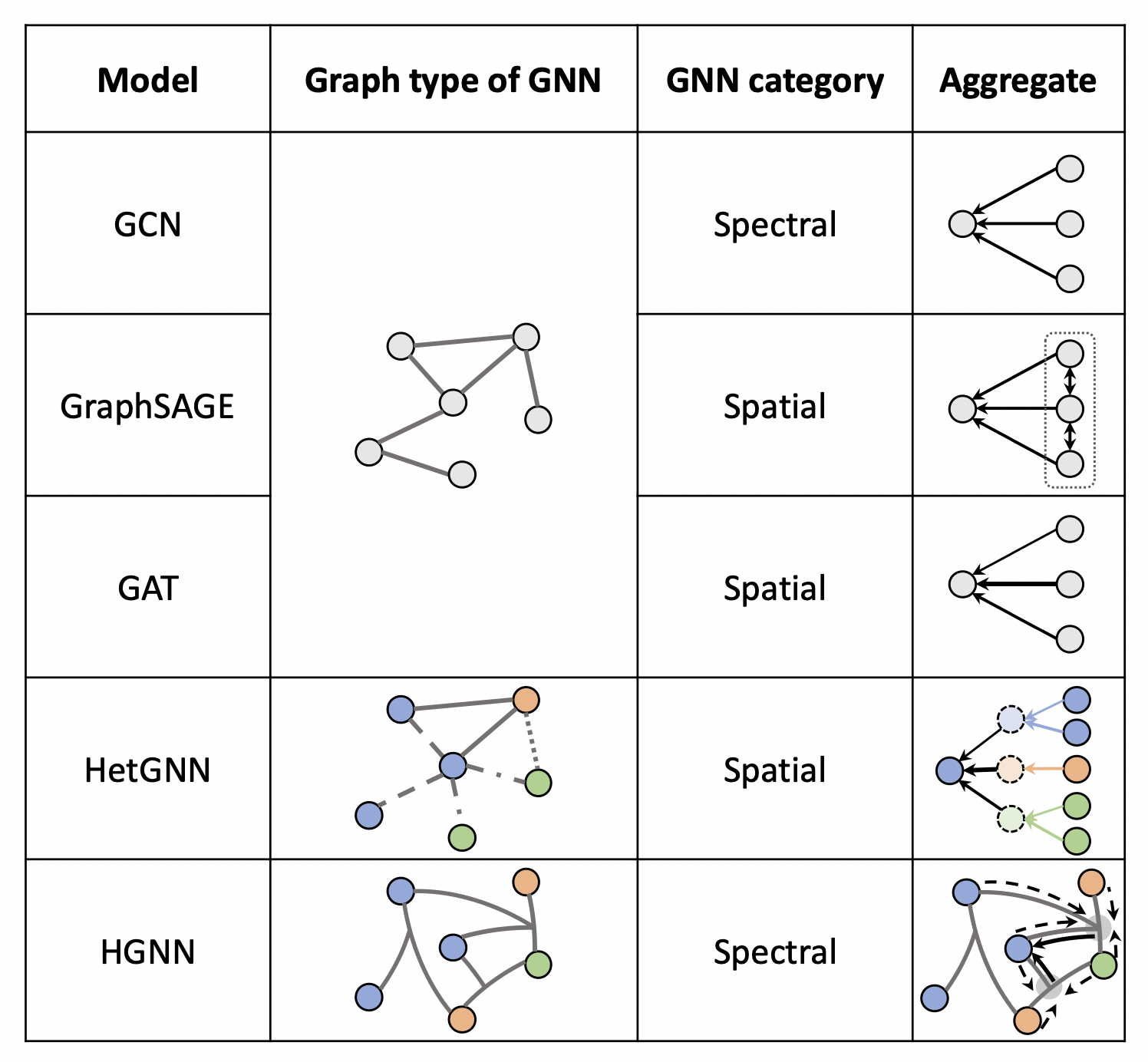
[출처] https://arxiv.org/pdf/2109.12843.pdf, Graph Neural Networks for Recommender Systems: Challenges, Methods, and Directions
GCN에서는 neighborhood aggregation할 때 단순히 주변 정점의 정보에 관해 sum 연산을 수행하고, 전체 그래프 구조를 반영하기 위해 인접 행렬 $A$를 사용한다. 그래서 GCN은 spectral 방법론에서 spatial 방법론을 사용했다고 앞서 설명했다. 그러나 GAT에서는 전체 그래프의 정보를 담는 인접 행렬을 사용하지 않아서 완전한 spatial 방법론에 해당된다.
GAT에서는 주변 정점의 정보를 가져올 때 각 이웃 정점마다 다른 attention을 부여하여 자기 자신을 업데이트한다. 이는 상식적으로 주변 정점들이 target 정점에게 모두 같은 영향력을 행사하는 경우는 드물다는 데서 유추할 수 있다. 즉, target 정점에게 가장 많은 영향력을 끼치는 정점에 더 큰 attention을 부여하고자 하는 게 GAT의 특징이다.
GAT와 Attention Coefficient
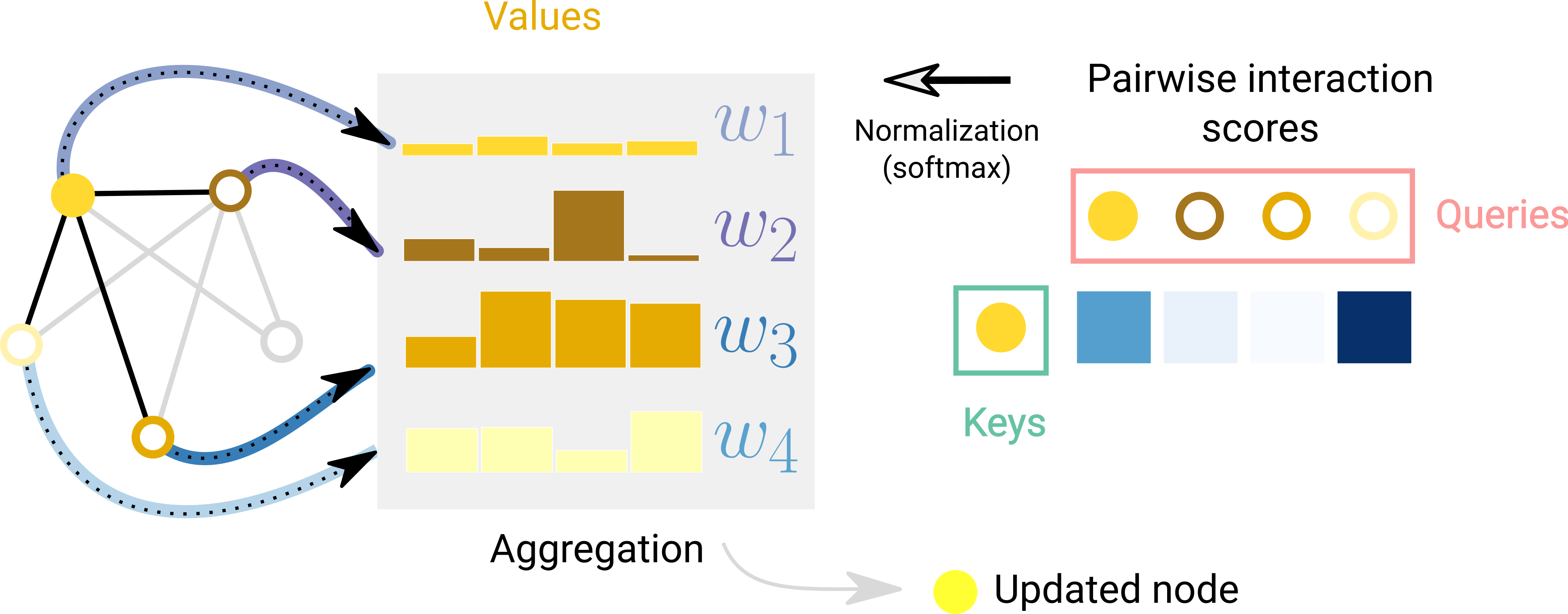
[출처] https://distill.pub/2021/gnn-intro, A Gentle Introduction to Graph Neural Networks
GAT에서는 GCN과 달리 인접 행렬 $A$ 대신 주변의 각 이웃 정점에 얼마나 주목할 것인지를 반영하기 위해 attention coefficient $a$를 사용한다. 다시 말해, 각 정점 간의 벡터를 참고해서 연산을 할 때 인접 정점 전체를 동일한 비율로 참고하는 것이 아니라 연관이 있는 정점에 좀 더 주의를 기울이겠다는 의미이다.
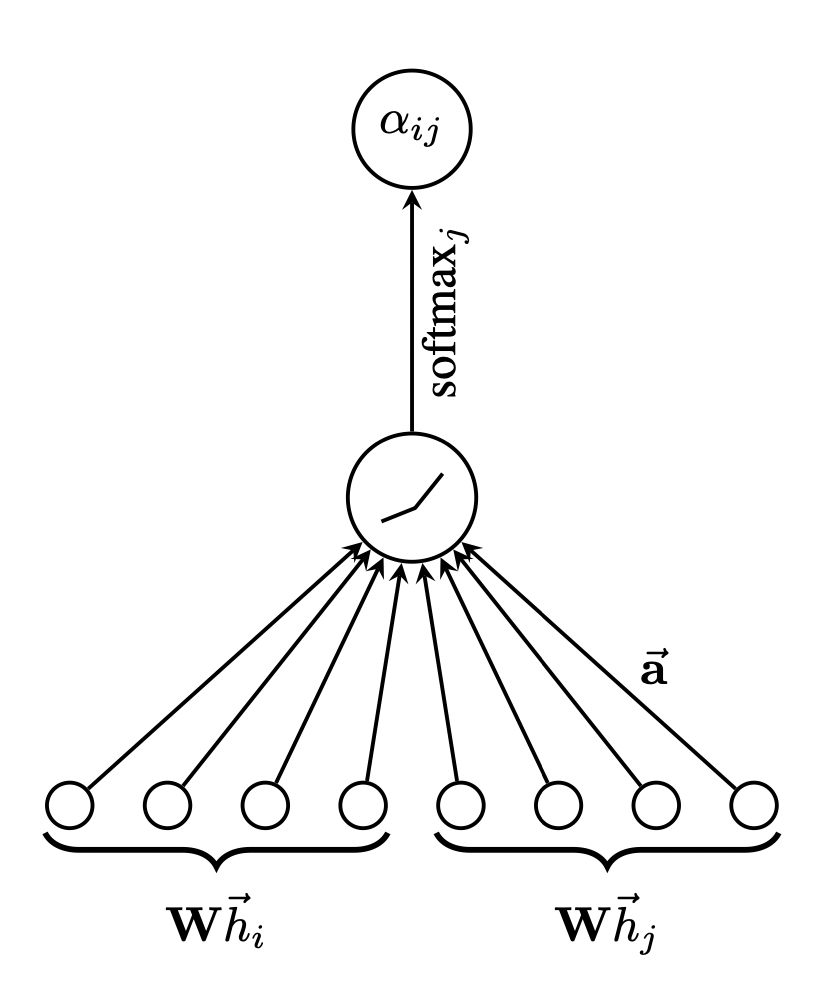
[출처] https://arxiv.org/pdf/1710.10903.pdf, Graph Attention Networks
정점 $i$와 $j$가 서로 이웃이고 정점 $i$에 관하여 주변 이웃 정점을 가지고 attention score를 구하려면, 우선 정점 $i$와 $j$의 hidden matrix에 가중치 파라미터를 곱해 feature transformation을 수행한다.
이를 가지고 MLP(Multi Layer Perceptron)에 input으로 넣어서 출력값 하나를 뽑을 수 있게 되는데, 마찬가지로 정점 $i$의 모든 이웃 정점에 관해 MLP에 넣어 출력값을 구한다. 그 출력값이 $e_{ij}$이며, 위의 식과 왼쪽 그림이 나타내는 것이 MLP에 넣어 정점 $i$을 기준으로 $j$에 대한 attention score를 구하는 것이다.
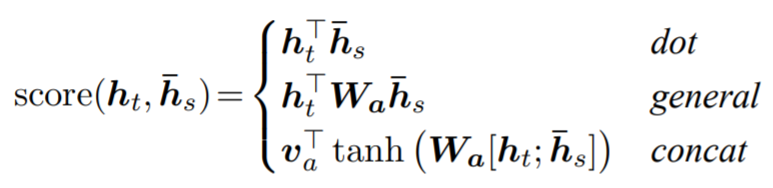
[출처] https://towardsdatascience.com/sequence-2-sequence-model-with-attention-mechanism-9e9ca2a613a, Renu Khandelwal
사실 dot-product self-attention만 있는 것이 아니라 어떤 두 token 또는 정점의 attention을 구하는 방법은 다양하다. 여기서는 세 번째 방법인 concatenation을 하여 MLP에 통과시키는 것을 사용했다.
Attention score를 구하는 다양한 방법과 self-attention의 의의에 관한 자세한 내용은 이전에 작성한 포스트를 참고하면 된다.
Attention 기법을 사용한 Seq2Seq with Attention
RNN 계열 모델인 LSTM을 여러개 이어서 encoder와 deocder로 만든 Seq2Seq에 관해 먼저 알아보고, 매 time step이 지날수록 이 Seq2Seq의 hidden state에 점차 많은 정보를 욱여넣게 되는 단점을 극복한 Seq2Seq with A
glanceyes.com
Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교
Transformer를 이해하려면 Seq2Seq with Attention 모델이 나오게 된 배경과 그 방법을 이해하는 것이 필요하다. 특히 transformer의 self-attention에 관해 한줄로 요약하면, Seq2Seq with Attention에서 decoder의 hidden st
glanceyes.com
이렇게 $i$에 관하여 모든 이웃 정점에 대하여 구한 attention score의 합은 가중 평균을 위해 1이 되어야 하므로 softmax를 적용한다.
GAT에서의 Multi Head Attention
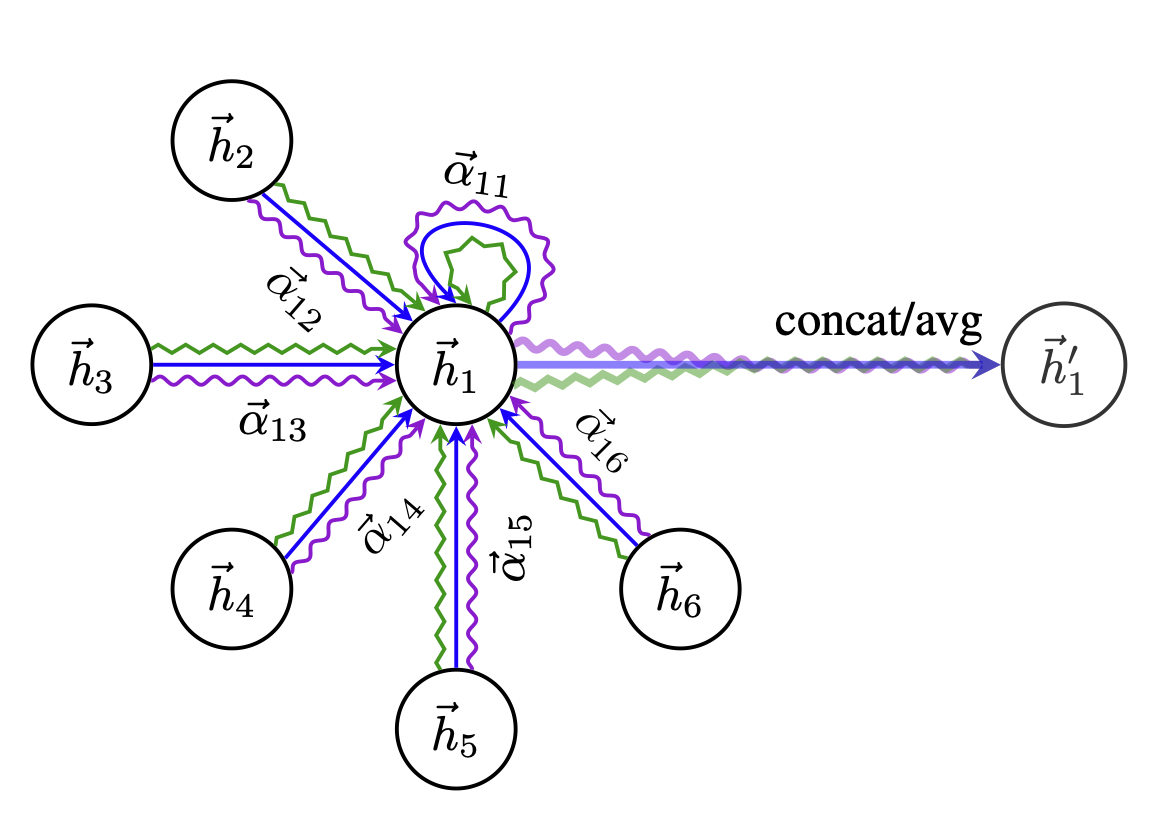
[출처] https://arxiv.org/pdf/1710.10903.pdf, Graph Attention Networks
GAT에서 Multi Head Attention은 attention score를 구하는 과정을 각 정점에 관해 여러 번 수행하는 것이며, 위의 오른쪽 그림에서 보라색, 파란색, 초록색의 구불구불한 선이 바로 정점 1에 관해 세 번 Multi Head Attention을 수행한 것이라고 볼 수 있다.
Multi Head Attention을 수행하는 방법에는 head 별로 계산한 결과의 평균을 구하는 방법과 concatenation하는 방법이 있다.
GAT의 특징
1. 인접한 정점에서 좀 더 연관된 정점에 더 많은 attention을 부여하여 임베딩 벡터 업데이트
2. 인접 행렬을 사용하지 않으므로 spatial 방법론에 해당
Neural Graph Collaborative Filtering(NGCF)
NGCF란?
NGCF는 그래프가 가진 장점을 활용하여 CF에서 유저-아이템 상호작용(Collaborative Signal)을 임베딩 레이어에서 직접 추출하여 파라미터에 반영할 수 있도록 하는 방법을 제시한 접근 모델이다.
Target 정점의 주변 이웃 정점으로부터 target 정점으로 메시지를 만들어서 전달(message passing)하고 이를 aggregation 하는 방법은 GCN과 유사하지만, 유저와 아이템 간의 상호작용을 이분 그래프(bipartite graph)로 구성하고 메시지를 만들 때 아이템과 유저 사이의 상호작용을 반영한다는 점이 차이라고 볼 수 있다.
기존에 유저와 아이템 데이터를 사용하는 학습 가능한 CF 모델의 핵심 두 가지를 정리하면 다음과 같다.
- 유저와 아이템의 임베딩을 잘 학습해야 한다.
- 유저와 아이템은 처음에 one-hot encoding으로 표현되고, 그것을 embedding layer를 통과하여 dense한 임베딩으로 표현한다.
- 유저와 아이템의 상호작용을 모델링한다.
- 예를 들어, MF에서는 유저와 아이템을 임베딩한 이후에 이를 내적하여 둘의 상호작용을 linear하게 표현한다.
하지만 기존의 신경망을 적용한 CF 모델들은 유저-아이템의 상호작용을 임베딩 단계에서 접근하지 못한다는 문제를 지닌다. 즉, 임베딩 학습 단계와 모델링 단계가 분리되어 있다. 예를 들어, Neural Collaborative Filtering에서도 임베딩이 일어난 이후에 임베딩을 concatenate하므로 임베딩과 상호작용 모델링이 분리되어 있음이 확인 가능하다.
즉, 유저와 아이템의 상호작용에 관한 latent factor 추출을 interaction function에만 의존하므로 결과적으로 sub-optimal한 임베딩을 사용하게 되어서 모델이 더 정확한 표현력을 가지지 못하는 단점이 있다.
NGCF는 이러한 유저와 아이템의 상호작용을 각 정점의 특징 임베딩 벡터를 업데이트하는 과정에서 반영할 수 있도록 한다.
NGCF의 학습 과정
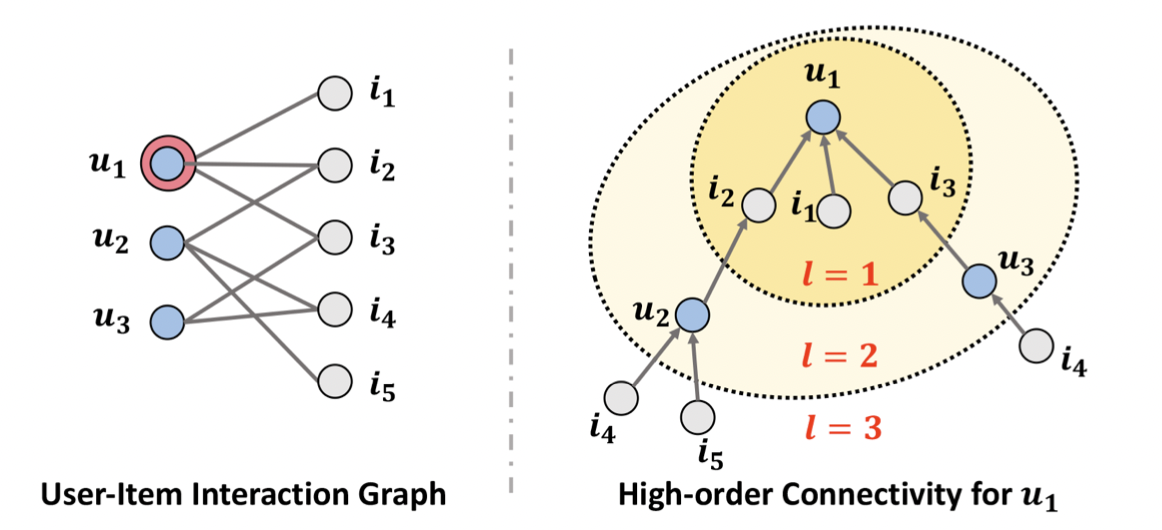
[출처] https://arxiv.org/pdf/1905.08108.pdf, Neural Graph Collaborative Filtering
앞서 말한 바와 같이 NGCF는 유저와 아이템 간의 상호작용(Collaborative Signal)을 이분 그래프로 만들고, 정점의 임베딩 벡터를 업데이트하는 과정에서 학습될 수 있도록 한다. 그러나 유저와 아이템 개수가 많아질수록 각 정점의 임베딩 벡터가 모든 상호작용을 학습하기에는 한계가 존재한다.
그래서 GNN을 통해 경로의 길이가 1보다 큰 연결의 High-Order Connectivity를 임베딩한다. High-Order Connectivity는 너무 어렵게 생각할 것 없이 GCN에서 여러 layer를 쌓아서 target 정점에 관해 몇 번 떨어진 이웃까지 볼 것인지와 비슷하다. Hop 또는 receptive field와 유사하다고 보면 된다.
위의 그림은 유저와 아이템의 상호작용 이분 그래프에서 유저 $u_1$을 target 정점으로 삼아 이를 tree 구조의 root로 고려하여 주변의 이웃 정점으로부터 메시지를 받아 aggregation 하는 과정을 그린 것이다.
유저 $u$에 관해 메시지를 aggregation 하는 과정은 GCN과 유사한데, self loop가 있다는 가정 하에 자기 자신으로부터 오는 메시지와 주변 이웃 아이템 정점으로부터 오는 메시지를 합친다.
주변 이웃 아이템 정점으로부터 오는 메시지를 만드는 과정(message contruction)을 식으로 나타낸 것이다.
$m_{u \leftarrow i} = \frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i}|}(\mathbf{W}_1 e_i)$까지만 보면 GCN과 유사한 것처럼 보이지만, 뒤의 유저와 아이템 간의 상호작용을 반영하는 $\mathbf{W}_2 (e_u \odot e_u)$이 있다는 것이 주목할 만하다.
이 두 번째 항이 추가되면서 유저와 유사한 아이템으로부터 메시지가 더 많이 오도록 한다.
자기 자신으로부터 오는 메시지는 자신의 임베딩 벡터 $e_u$에다가 공유하는 가중치 파라미터인 $\mathbf{W}_1$를 곱하면 된다.
NGCF 전체 구조
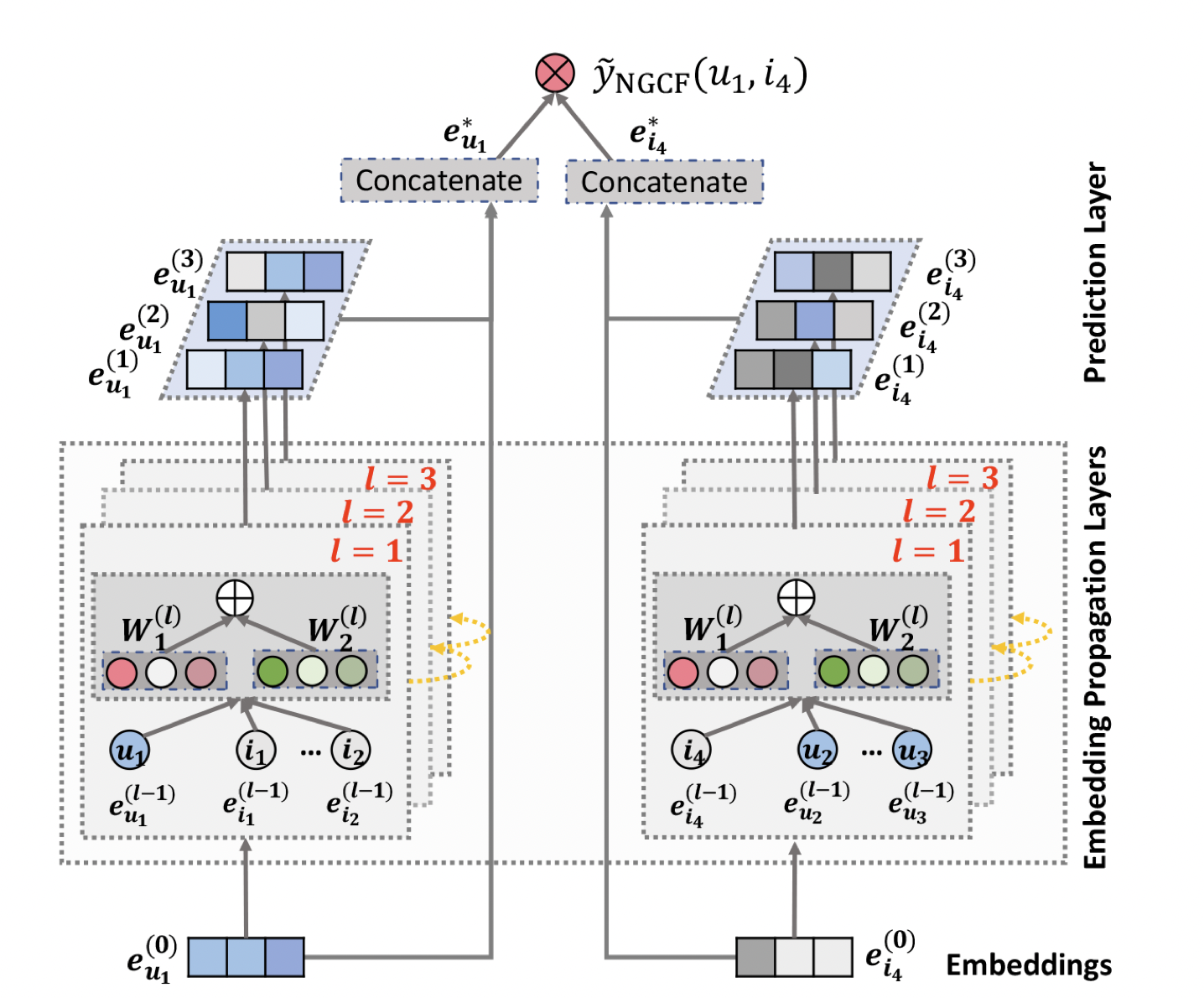
[출처] https://arxiv.org/pdf/1905.08108.pdf, Neural Graph Collaborative Filtering
위의 NGCF의 예시는 유저 $u_1$이 아이템 $i_4$를 얼마나 선호할지를 예측하는 것을 나타낸 것이다.
이처럼 NGCF의 전체적인 구조 관점으로 각 레이어에서 어떠한 과정이 일어나고 어떻게 식을 정의할 수 있는지를 정리해보자.
임베딩 레이어(Embedding Layer)
유저와 아이템의 one-hot encoding을 $k$차원으로 임베딩하는 유저-아이템의 초기 임베딩을 제공한다.
$e_u$: 유저 $u$에 해당되는 정점에 대한 임베딩
$e_i$: 아이템 $i$에 해당되는 정점에 대한 임베딩
기존 MF(Matrix Factorization), Neural CF 모델에서는 one-hot encoding 벡터를 embedding layer로 임베딩시켰던 것이 곧바로 interaction function에 입력되어 선호도를 예측한다.
그러나 NGCF에서는 이 임베딩을 GNN 상에서 전파시켜 정제(refine)시킨다. 쉽게 말하면 앞에서 계속 말한 것처럼 각 정점의 임베딩 벡터를 업데이트 하는 과정이 모델링 단계에 존재한다는 걸 뜻한다. 이는 임베딩 레이어에서 각 정점의 임베딩 벡터를 업데이트할 때 유저와 아이템 간의 collaborative signal을 명시적으로 주입하기 위한 과정이다.
임베딩 전파 레이어(Embedding Propagation Layer)
Target 정점에 관하여 몇 번 건너 뛴 이웃 정점의 정보까지 반영하는 High-Order Connectivity를 학습한다. 유저와 아이템 간의 collaborative signal(또는 interaction 정보)을 담을 메시지를 구성(message construction)하고 결합(aggregation)하는 단계라고도 볼 수 있다.
Message Construction
유저-아이템 간의 affinity(관련성)를 고려할 수 있도록 메시지를 구성한다. 즉, 앞서 말한 바처럼 메시지 구성 시 유저와 아이템 간의 상호작용을 반영한다. 유저와 연결된 아이템의 수가 많을수록 이 메시지의 크기가 커지는데, 이를 정규화하기 위해 개별 메시지의 크기를 이웃한 정점의 개수로 나누어준다. 또한 여기서 가중치 $W$를 사용하고, 이를 매번 메시지를 구성할 때마다 공유하는 weight sharing이 발생한다.
$\mathbf{W}_1$, $\mathbf{W}_2$: weight matrix
$\odot$: element-wise production
$\mathcal{N}_u$, $\mathcal{N}_i$: 유저, 아이템의 이웃한 유저, 아이템 집합
Message Aggregation
$u$의 이웃 노드로부터 전파된 message들을 결합하면 1-hop 전파를 통한 임베딩이 완료된다. 이후 자신으로부터 전달되는 메시지와 인접 노드들로부터 전달되는 메시지를 합해서 Leaky ReLU를 통과시킨다.
Higher-Order Propagation
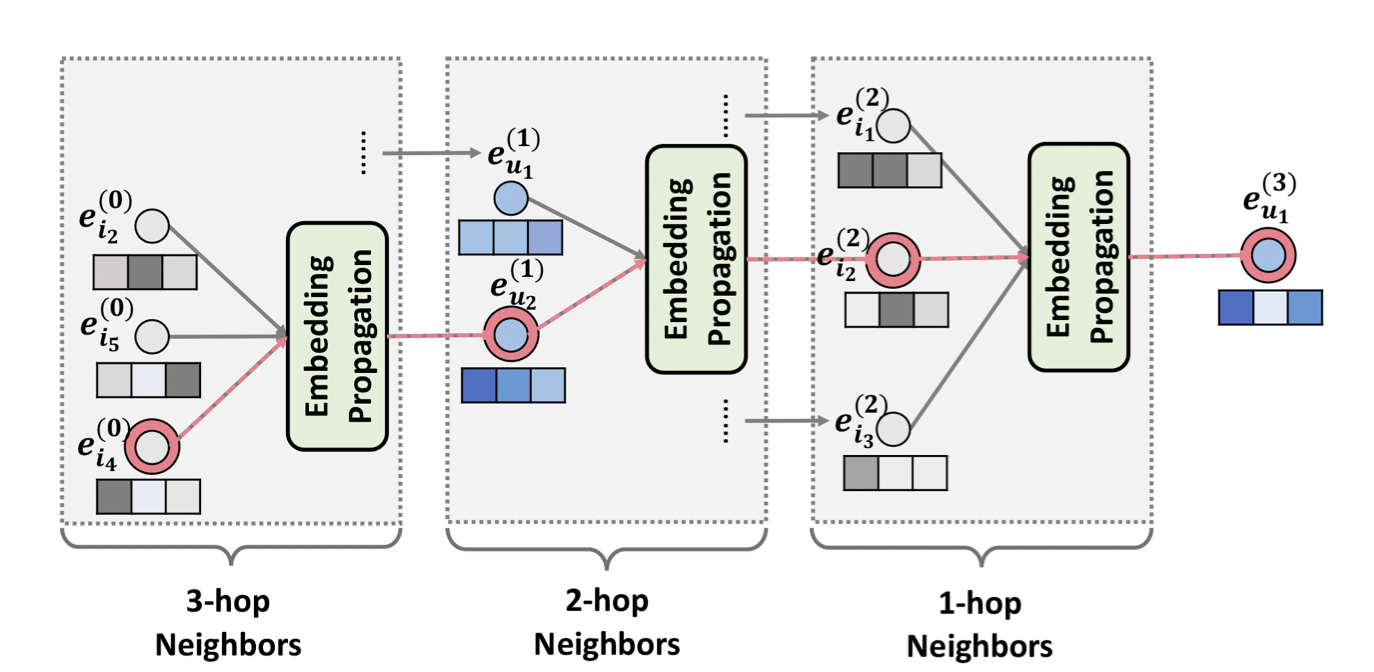
[출처] https://arxiv.org/pdf/1905.08108.pdf, Neural Graph Collaborative Filtering
위의 사진은 3개의 레이어를 쌓아서 만든 3-hop layer의 메시지 구성, 전파, 그리고 aggregation 과정을 나타낸 것이다. 이처럼 $l$개의 임베딩 전파 레이어를 쌓으면, 유저 정점은 $l$-차 이웃으로부터 전파된 메시지까지 모두 이용할 수 있다.
$l$단계에서 유저 $u$의 정점 임베딩 벡터는 $(l - 1)$ 단계의 임베딩을 통해 업데이트 된다.
유저의 아이템 선호도 예측 레이어(Prediction Layer)
NGCF에서는 서로 다른 임베딩 전파 레이어에서 학습된 임베딩 벡터를 concatenate하는데, 유저와 아이템 별로 $L$차 까지의 임베딩 벡터를 concatenate하여 최종 임베딩 벡터를 계산한다. 이후 유저-아이템 벡터를 내적하여 최종 선호도 예측값을 계산한다.
실제 네이버 부스트캠프 AI Tech의 Level 2 DKT 과제 코드에서는 이 부분을 내적으로 하지 않고 broadcasting을 고려한 element-wise 곱셈을 진행하여 나중에 합치는 방식으로 진행했는데, 이는 바로 위의 식에서 유저의 최종 임베딩 벡터와 아이템의 최종 임베딩 벡터를 내적하는 것과 결과적으로 동일하기 때문이다.
'''
u_emb: 유저와 최종 임베딩 벡터
p_emb: Positive item(유저와 상호작용 있었던 아이템)의 최종 임베딩 벡터
y_NGCF(u,i) = e_u*^T \cdot e_i* 식을 pytorch의 element-wise 곱셈 연산과 sum으로 구현한 것이다.
'''
y_ui = torch.mul(u_emb, p_emb).sum(dim = -1)
NGCF의 특징
[출처] https://arxiv.org/pdf/1905.08108.pdf, Neural Graph Collaborative Filtering
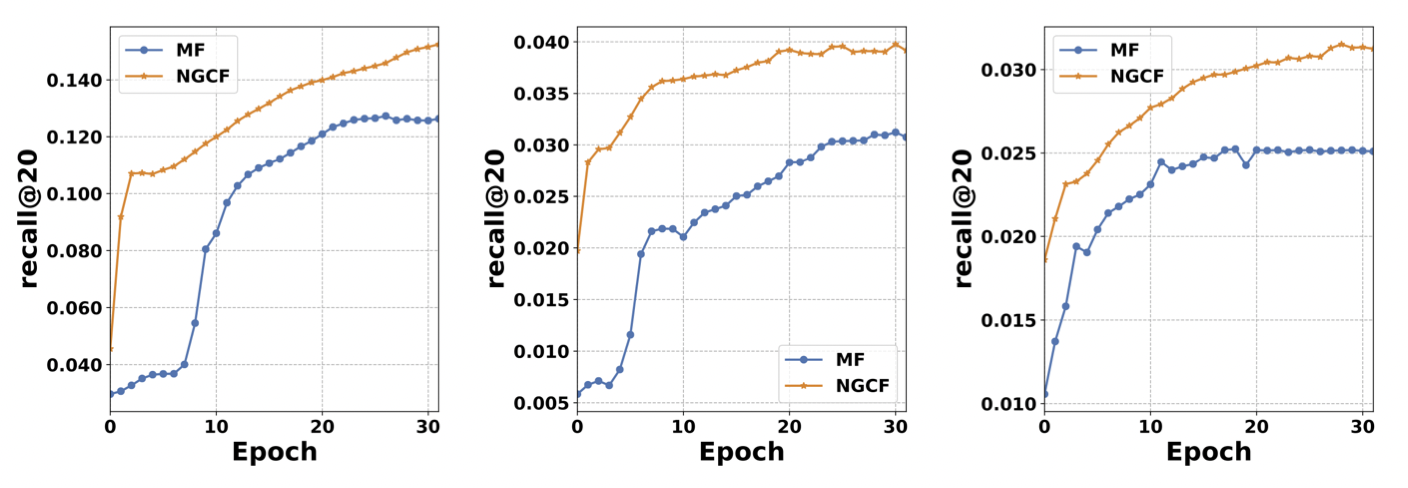
논문에서 사용한 데이터셋에 의하면 임베딩 전파 레이어가 많아질수록 모델의 추천 성능이 향상되는 것을 볼 수 있다. 다만, 레이어가 너무 많이 쌓이면 앞서 설명한 over-smoothing이 발생할 수 있어서 대략 $L=3, 4$일 때 좋은 성능을 보인다고 알려져 있다.
Model capacity가 크고 임베딩 전파를 통해 representation power가 좋아져서 학습 과정에서 MF보다 더 빠르게 수렴하고 recall도 높다는 특징을 지닌다. 또한 MF와 비교하여 유저와 아이템의 상호작용이 임베딩 공간에서 더 명확하게 반영되며, 레이어가 많아질수록 더 명확해진다.
NGCF의 특징
1. 유저와 아이템에 관해 이분 그래프 사용
2. 메시지 구성할 때 유저와 아이템의 상호작용 반영하기 위한 파라미터를 공유하여 사용
3. 서로 다른 임베딩 전파 레이어에서 학습된 임베딩 벡터를 concatenation 하여 최종 값 예측
LightGCN
LightGCN이란?
LightGCN은 GCN의 가장 핵심적인 부분만 사용한 모델이며, 이를 위해 핵심적이지 않은 부분을 제거하고 다른 방법을 사용했다.
주변 이웃 노드로부터 메시지를 target 정점으로 전달할 때 $W_1 e_i$처럼 공유하는 가중치 파라미터를 곱하는 feature transformation 과정을 제거하고 단순히 normalized sum을 하는 과정으로 구현했다.
또한 정점 임베딩 벡터를 업데이트하기 위해 주변 정점으로부터 aggregation하는 과정에서 NGCF는 non-linear activation 함수인 LeakyReLU를 사용했지만, LightGCN은 비선형성을 부여하는 활성 함수(activation function)를 사용하지 않았다.
그리고 마지막에 각 임베딩 전파 레이어에서 나오는 하나의 정점에 관한 임베딩 벡터들을 concatenation 하지 않고 가중 합 하는 과정으로 변경했다.
LightGCN의 아이디어
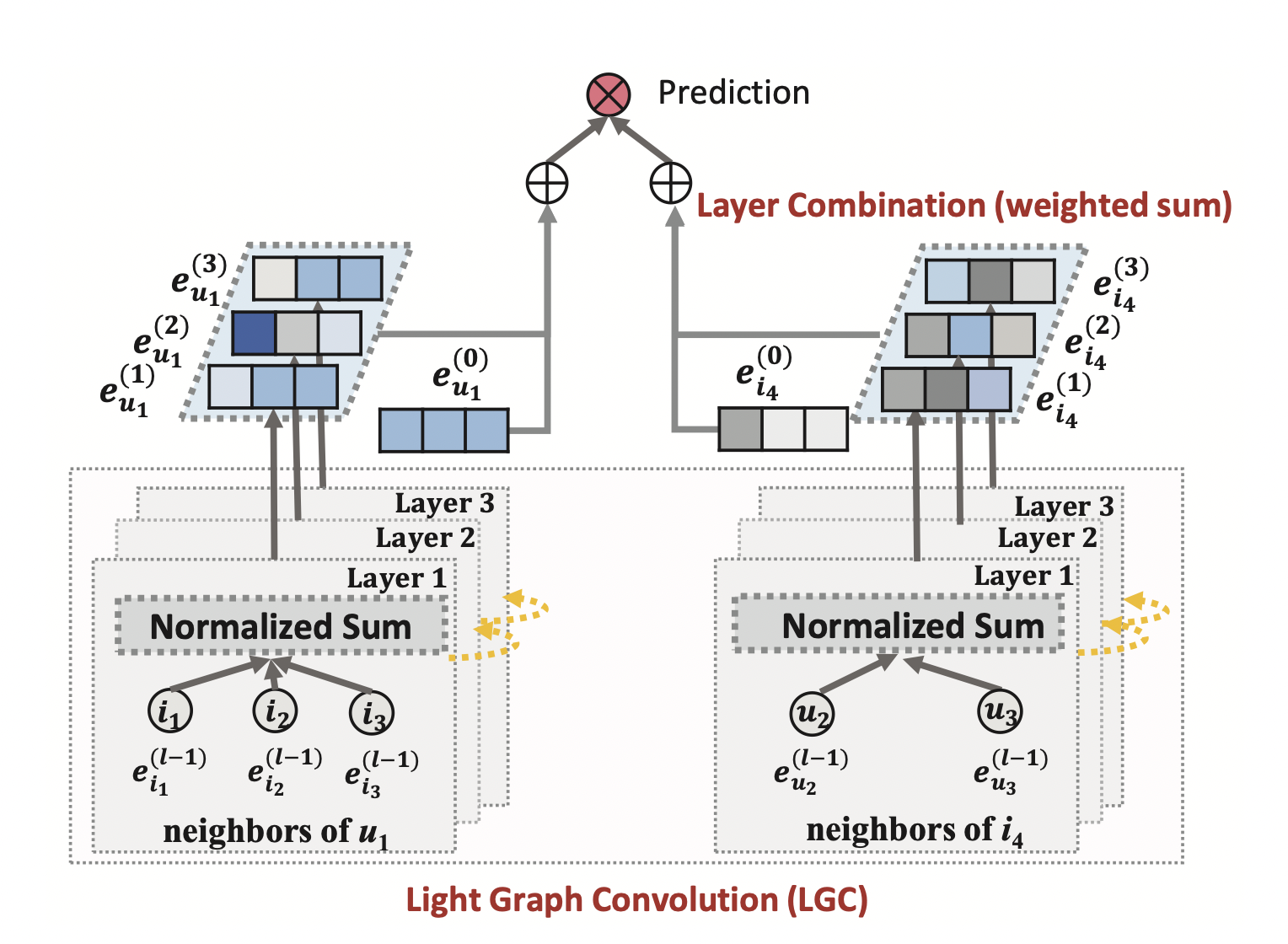
[출처] https://arxiv.org/pdf/2002.02126.pdf, LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
가벼운 message construction과 aggregation
기존 NGCF 모델은 임베딩 전파 레이어에서 메시지를 전달할 때 매번 가중치인 학습 파라미터를 임베딩 벡터에 곱하고, 거기에 non-linear transformation인 LeakyReLU를 사용하여 정점의 임베딩 벡터를 업데이트한다.
반면에 LightGCN에서는 target의 이웃 정점의 임베딩 벡터를 가중합 하는 것이 메시지 전달과 aggregation 과정의 전부여서 학습 파라미터 수와 연산량이 감소한다.
Layer Combination (Weighted Sum)
레이어가 깊어질수록 강도가 약해질 것이라는 아이디어를 적용하여 모델에서 한 정점에 관한 각 레이어의 임베딩 벡터를 최종 임베딩으로 합치는 부분을 단순화했는데, NGCF에서는 concatenation 했지만 여기서는 가중 합(weighted sum)을 적용한다.
LightGCN의 전파 규칙
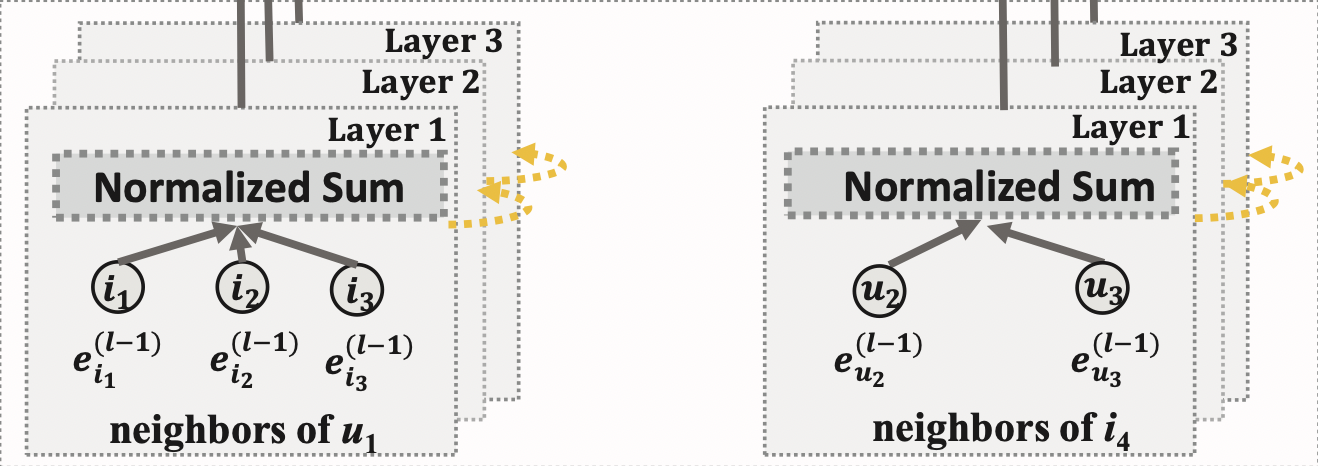
[출처] https://arxiv.org/pdf/2002.02126.pdf, LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
Feature transformation과 nonlinear activation을 제거하고 가중 합으로 GCN을 적용한다.
앞에서 말한 바처럼 LightGCN에서는 $\mathbf{W}_1^{(k)} e_i^{(k-1)}$와 같은 feature transform이 존재하지 않는다. 또한 NGCF와는 달리 self-loop를 가정하지 않아서 자기 자신을 제외하고 주변의 이웃 정점만 메시지 aggregation에 사용하기 때문에 $\mathbf{W}_1^{(k)} e_u^{(k-1)}$ 항이 뜻하는 self-connection이 존재하지 않는다. 그리고 NGCF에서 사용했던 유저와 아이템의 상호작용을 반영하는 $\mathbf{W}_2^{(k)} (e_i^{(k-1)} \odot e_u^{(k-1)}$도 없다.
LightGCN의 예측 레이어(Layer Combination)
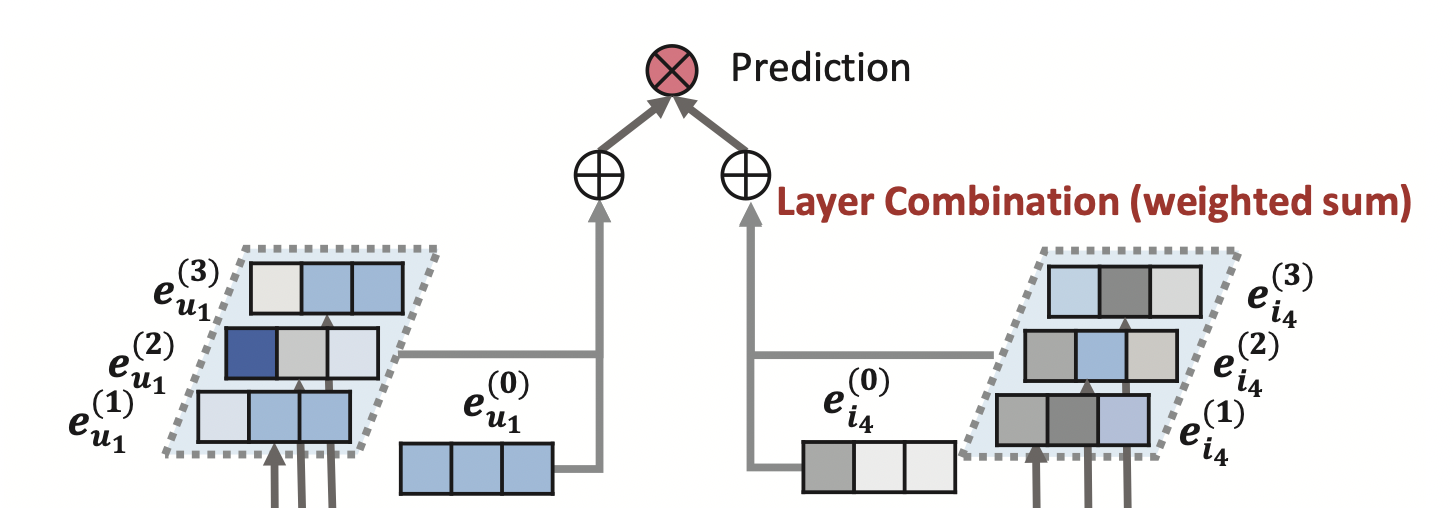
[출처] https://arxiv.org/pdf/2002.02126.pdf, LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
LightGCN에서는 최종 예측을 위해 한 정점에 관한 각 레이어의 임베딩을 결합하는 방법으로 가중 합(weighted sum)을 사용하는데, 이는 각 레이어의 임베딩 결과를 concatenation하는 NGCF와의 차이점 중 하나이다.
아래 식은 $k$-층으로 된 레이어의 임베딩을 각각 $\alpha_k$배 하여 가중합으로 각 유저 또는 아이템 정점에 관한 최종 임베딩 벡터를 계산하는 것이다.
여기서 $\alpha_k$는 최종 임베딩 벡터를 만들 때 가중 합에 사용하는 $k$-층 임베딩의 가중치이며, 하이퍼 파라미터 또는 학습 파라미터로 둘 다 설정이 가능하다. 예를 들어, $\alpha_k$를 하이퍼 파라미터처럼 $(k + 1)^{-1}$로 설정할 수 있는데, 이때는 레이어 층이 더 깊어질수록 강도가 낮아짐을 수식으로 반영한 것이다.
레이어가 깊어지면 앞서 말한 것처럼 over-smoothing이 발생할 수 있고, 이를 해결하고자 단순히 마지막 레이어만 사용하는 것도 문제일 수 있다. 그러나 다른 레이어에서 나온 임베딩 벡터 결과는 다른 semantic을 포착할 수 있으며, 레이어가 깊어질수록 Higher Order Connectivity(Interaction)을 포착할 수 있으므로 무조건 레이어를 얕게 사용하는 것도 좋지 않다.
LightGCN에서는 임베딩 벡터를 업데이트할 때 메시지를 aggregation 하는 과정에서 self-connection을 사용하지 않았는데, 이 layer combination 과정에서 self-connection의 효과가 나타난다.
LightGCN의 특징
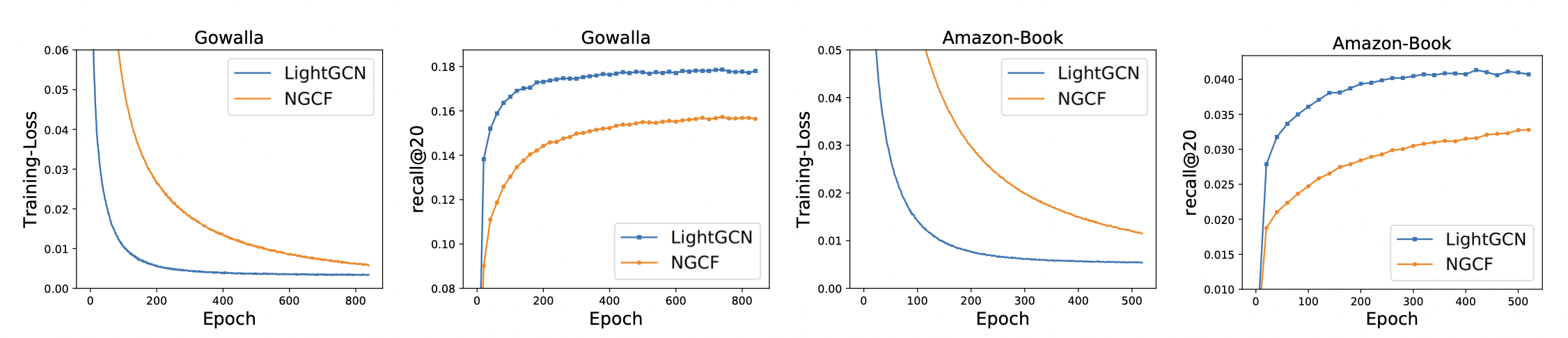
[출처] https://arxiv.org/pdf/2002.02126.pdf, LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
논문에서 Gowalla, Yelp2018, Amazon-Book 데이터셋을 가지고 NGCF과 LightGCN을 실험한 결과, 학습 과정에서의 loss와 추천 성능 모두 LightGCN이 NGCF보다 뛰어나다는 걸 볼 수 있다. 또한 LightGCN은 NGCF보다 Training loss가 낮으면서 추천 성능이 좋은 것을 볼 수 있는데, 이는 해당 데이터셋에 관해 모델의 일반화 성능이 좋다고 해석할 수 있다.
LightGCN의 특징
1. NGCF에서 메시지 구성과 전달 시 파라미터를 공유하여 사용하는 대신 인접 정점 임베딩에 관해 가중 합 사용
2. 메시지를 aggregation 할 때 NGCF처럼 LeakyReLU 사용하지 않음
3. 최종 예측 시 NGCF처럼 concatenation 하지 않고 가중 합 사용
출처
1. 네이버 커넥트재단 부스트캠프 AI Tech RecSys Track 이영수 마스터님 DKT 대회 강의
2. 서강대학교 CSE4152 고급소프트웨어실습1 Lab 7 Graph 기반 문제 풀이
업데이트
1. Spectral 방법론의 설명의 부족한 부분을 추가하고 일부 내용이 수정되었습니다. (2023. 04. 12)
'AI > 추천 시스템' 카테고리의 다른 글
| 신경망을 사용한 Matrix Factorization 모델과 NeuMF(Neural Collaborative Filtering) (1) | 2022.07.10 |
|---|---|
| 추천 시스템의 평가 방법과 실험에서의 데이터 분할 전략 (0) | 2022.04.26 |
| Side Information과 이를 사용하는 추천 시스템 (1) | 2022.04.20 |
| Deep Learning 기반의 Collaborative Filtering (0) | 2022.04.18 |
| 추천 시스템에서의 Implicit Feedback (0) | 2022.04.18 |
소중한 공감 감사합니다.