신경망을 사용한 Matrix Factorization 모델과 NeuMF(Neural Collaborative Filtering)
- -
신경망을 사용한 Matrix Factorization
Matrix Factorization
추천 시스템에서 사용자와 아이템의 상호작용 행렬의 잠재 요인을 학습하기 위해 낮은 차원을 지닌 행렬 곱으로 분해하는 Matrix Factorization 방법이 기본적인 협업 필터링 모델로 자주 쓰인다.
Matrix Factorization은 두 행렬 곱으로 나타내서 학습 데이터에 관해 잠재 요인을 학습하고 다시 이를 곱하여 원상태로 복원할 때 원래 학습 입력 데이터와 얼마나 유사한지 그 차이를 줄이는 방향으로 학습한다.
그래서 상호작용이 없거나 적은 유저의 새로운 상호작용 데이터가 들어왔을 때 Matrix Factorization을 통과하여 복원되는 결과를 가지고 해당 사용자가 어떠한 아이템을 소비하거나 관심을 가질지를 예측하는 것이다.
이를 neural network를 사용하여 구현하면 어떤 구조를 가지고, 각 부분이 실제 Matrix Factorization에서 어떠한 의미와 역할을 지니는지를 분석할 필요가 있어 보였다.
이전에 포스팅한 Matrix Factorization에 관한 자세한 내용은 다음 글에서 확인할 수 있다.
https://glanceyes.tistory.com/entry/추천-시스템-MBCF와-SVD를-응용한-MFMatrix-Factorization
모델 기반 CF와 SVD를 응용한 MF(Matrix Factorization)
Model-based Collaborative Filtering(MBCF) NBCF(Neighborhood-based CF)의 한계 Sparsity(희소성) 문제 데이터가 충분하지 않으면 추천 성능이 떨어져서 유사도 계산이 부정확한 문제가 있다. 데이터가 부족하거나 또
glanceyes.com
Maxtrix Factorization 신경망 모델 구조

$M$명의 사용자와 $N$개의 아이템이 존재하고, $M$명의 사용자가 $N$개의 아이템에 관해 explicit 또는 implicit feedback을 남긴 상호작용 행렬이 존재한다고 가정한다.
또한 Matrix Factorization을 사용하여 $K$ 차원의 잠재 공간에서 사용자와 아이템에 내재된 잠재 요인을 학습한다고 가정한다.
위의 그림은 Matrix Factorization을 신경망 모델로 표현하여 나타낸 것이며, 각 레이어와 요소가 실제 Matrix Factorization에서 어떠한 역할을 하는지를 도식화했다.
Input Layer

- 각 사용자와 아이템으로부터 입력을 받는 부분
- One-hot Representation(One-hot Encoding)이 입력으로 들어온다.
- 예) M명의 사용자가 있을 때, 두 번째 사용자에 대한 One-hot Representation
- { 0, 1, 0, … , 0 } ⇒ 두 번째 원소만 1이고 나머지는 $M-1$개의 원소는 0인 상태
- 예) N개의 아이템이 있을 때, $N-1$번째 아이템에 대한 One-hot Representation
- { 0, 0. … , 1, 0 } ⇒ $N-1$번째 원소만 1이고 나머지 $N-1$개의 원소는 0인 상태
- 사용자와 아이템 모두 마찬가지로 적용된다.
- 예) M명의 사용자가 있을 때, 두 번째 사용자에 대한 One-hot Representation
Input layer는 사용자와 아이템 행렬을 입력으로 받는 부분이며, 위의 그림은 Matrix Factorization에서 내적을 구하고자 하는 사용자와 아이템을 입력 벡터로 사용하는 모습이다.
이때, 사용자와 아이템의 각 행렬은 one-hot encoding 형태의 벡터로 구성된다.
각 사용자 벡터는 전체 $M$명의 학생 중에서 구분될 수 있도록 하나의 원소만 1이고 나머지 원소는 모두 0이며, 이는 $N$개의 아이템 벡터에 관해서도 모두 마찬가지다.
사실 여기서는 입력으로 주어지는 사용자와 아이템 벡터를 one-hot encoding된 벡터로 나타내는 것으로 표현했지만, 사용자 또는 아이템에 관한 side information이 존재하고 이를 통해 각 사용자와 아이템이 구별되도록 표현할 수 있으면 side information을 사용하여 입력 벡터에 concatenation 하여 임베딩 레이어에 입력으로 넣을 수도 있다.
Embedding Layer
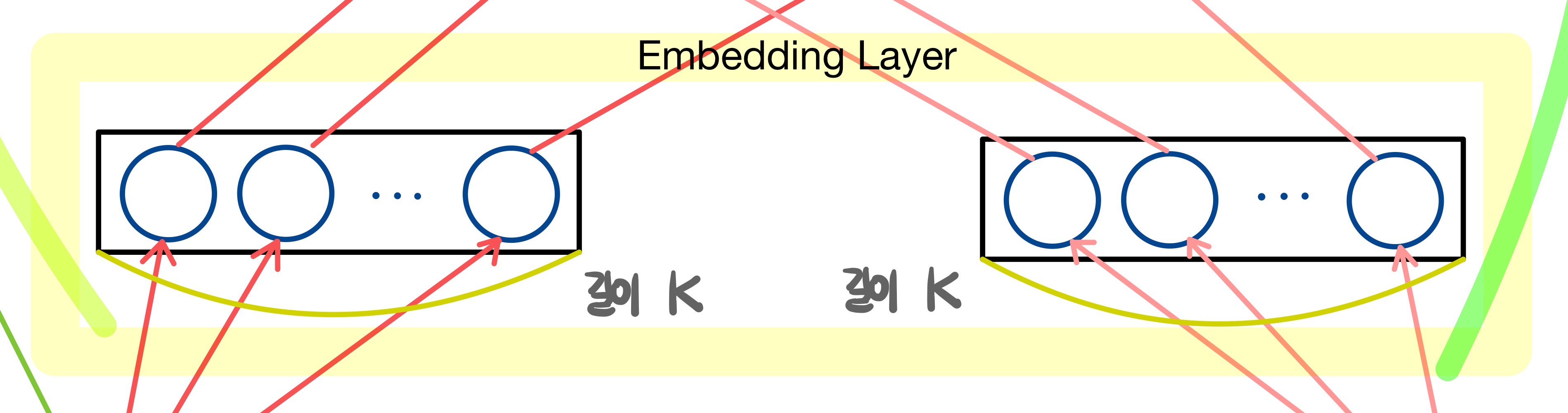
- 사용자와 아이템에 관한 잠재요인을 추출하는 부분
- 사용자와 아이템 각각에 대한 잠재요인 $K$개를 추출하기 위해 두 개의 Embedding Layer로 구성
- $K$개의 잠재요인을 추출한다면 Embedding Layer는 $K$개의 노드로 구성된다.
- $K$개의 노드가 각각 모든 유저에 대한 One-hot Encoding과 연결
- 마치 기존 MF에서 행에 해당되는 한 명의 사용자 또는 아이템에 관해 $K$개의 저차원의 원소로 표현되는 것과 동일하다.
앞서 만든 one-hot encoding된 사용자와 아이템 입력 벡터 쌍을 각각 임베딩 레이어에 통과시켜서 $K$ 차원 공간으로 보내는 과정을 거치는 곳이다.
사용자와 아이템 벡터를 모두 $K$ 차원으로 보내는 것은 Matrix Factorization에서 행 또는 열이 $K$ 차원을 지니는 두 개의 행렬 곱으로 나타내는 과정과 대응된다.
Element-wise Product Layer

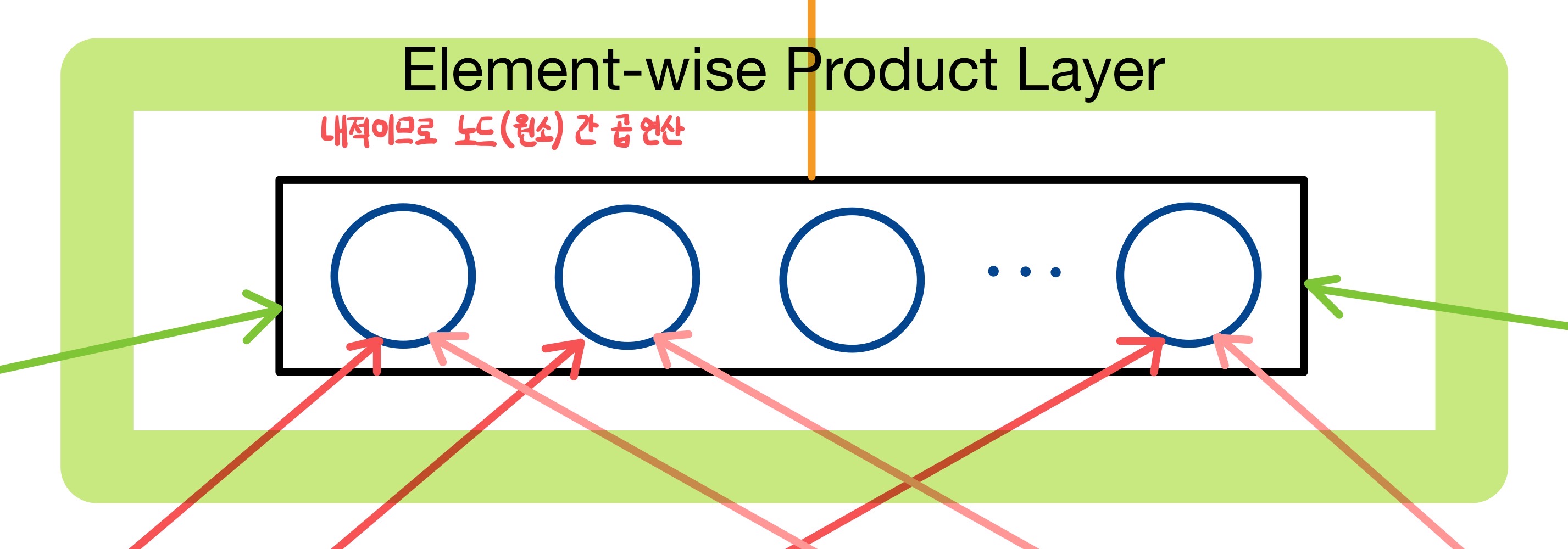
- Embedding Layer의 사용자와 아이템의 잠재 요인에 관한 내적 연산을 위해 존재한다.
- 마치 MF에서 $P×Q^T$ 행렬 연산을 수행하는 것과 같다.
- 사용자와 아이템의 잠재 요인은 모두 $K$개의 원소로 되어 있으므로 내적 연산이 가능
- 한 사용자의 하나의 아이템에 대한 compatibility를 구하는 내적의 결과 값은 scalar이므로 이것이 사용자와 아이템에 대한 평점 또는 선호도를 나타내는 값으로 볼 수 있다.
- Implicit feedback이라면 해당 사용자가 그 아이템에 어느 정도의 관심을 지니는지에 관한 정도로 판단할 수 있다.
Matrix Factorization에서 $K$ 차원을 지니는 사용자 또는 아이템 벡터를 행렬 곱할 때 각 원소끼리 곱하여 내적을 수행한다.
이는 신경망에서 embedding layer를 통과한 $K$ 차원의 사용자와 아이템 벡터 쌍을 element-wise product 하는 연산이다.
Prediction Layer

- Element-wise Product Layer의 연산 결과는 사용자 또는 아이템마다 상이한 절댓값을 지닐 가능성이 높다.
- 예) 사용자 $A$와 아이템 $a$에 대한 예측 결과 값은 1.2, 아이템 $b$에 대한 예측 결과 값은 -5일 수 있다.
- Sigmoid 함수 등 0에서 1 사이로 compatibility에 대한 예측을 나타낼 수 있는 값으로 바꾸기
- 예) 사용자 $A$가 아이템 $a$를 좋아할 확률 0.7, 아이템 $b$를 좋아할 확률 0.05
- Keras에서는 Flatten Layer 사용 가능
사용자 벡터와 아이템 벡터를 element-wise 한 결과는 어떠한 scalar 값을 지니는데, 이는 해당 사용자가 그 아이템에 관해 얼마나 많은 관심을 지닐지에 관한 정도로 해석할 수 있다.
이를 0에서 1 사이의 확률 값으로 나타내고 비선형성을 부여하고자 sigmoid 등 활성 함수를 통과시키면 사용자의 아이템에 관한 선호도 또는 구매 예측 확률을 예측할 수 있다.
사용자와 아이템에 대한 Bias 추가 학습

- 모든 사용자에 대한 입력 정점 $M$개와 연결된 하나의 정점 추가
- 사용자의 평점 또는 선호도에 대한 편차를 학습
- 모든 아이템에 대한 입력 정점 $N$개와 연결된 하나의 정점 추가
- 아이템의 평점 또는 선호도에 대한 편차를 학습
- Element-wise Product Layer에서의 결과와 학습한 사용자와 아이템 Bias 결과 값을 더한다.
- 전체 평점을 모델이 학습하는 건 복잡하다.
- 데이터를 신경망에 넣기 전에 전체 평균을 일률적으로 빼주고 나중에 산출된 예측치에 일률적으로 더하는 방식이 유리하다.
Explicit feedback에서 어떤 사용자는 전반적으로 아이템에 관해 평점을 후하게 주는 경우가 있고, 또 어떠한 사용자는 박하게 주는 경우도 있다.
이는 implicit feedback에서도 마찬가지이며 아이템 관점에서도 선호도에 bias가 생길 수 있는데, 이러한 사용자 또는 아이템의 경향성을 반영하고자 bias를 적용하면 다음과 같다.
$b$: 전체 평점 평균
$bu_x$: 전체 평균을 제거한 후 사용자 $x$의 평가 경향 (사용자 $x$의 평점 평균과 전체 평균의 차이)
$bi_y$: 전체 평균을 제거한 후 아이템 $y$의 평가 경향 (아이템 $y$의 평점 평균과 전체 평균 차이)
모든 사용자에 대한 입력 정점 $M$개와 연결된 하나의 정점을 추가한 것이 바로 사용자의 평가 경향인 $bu_x$를 학습하기 위한 부분이다.
마찬가지로 모든 아이템에 대한 입력 정점 $N$개와 연결되어 추가된 정점은 아이템의 평가 경향인 $bi_y$를 학습하기 위한 부분이다.
또한 $bu_x$와 $bi_y$를 element-wise Product layer에서 내적한 결과와 더하는 것이 바로 위의 식에서 $bu_x + bi_y + \sum_{k=1}^{K} p_{xk} q_{ky}$의 계산 과정이다.
신경망에서 전체 평균을 구하는 식은 상대적으로 복잡하므로 이를 backpropagation하여 파라미터를 업데이트할 때 어려움이 따른다.
따라서 입력 데이터를 신경망에 넣기 전에 전체 평균을 일률적을 빼고, 나중에 산출된 예측치에 일률적으로 더해주는 방식을 적용한다.
NeuMF(Neural Collaborative Filtering) Multi Layer Perceptron
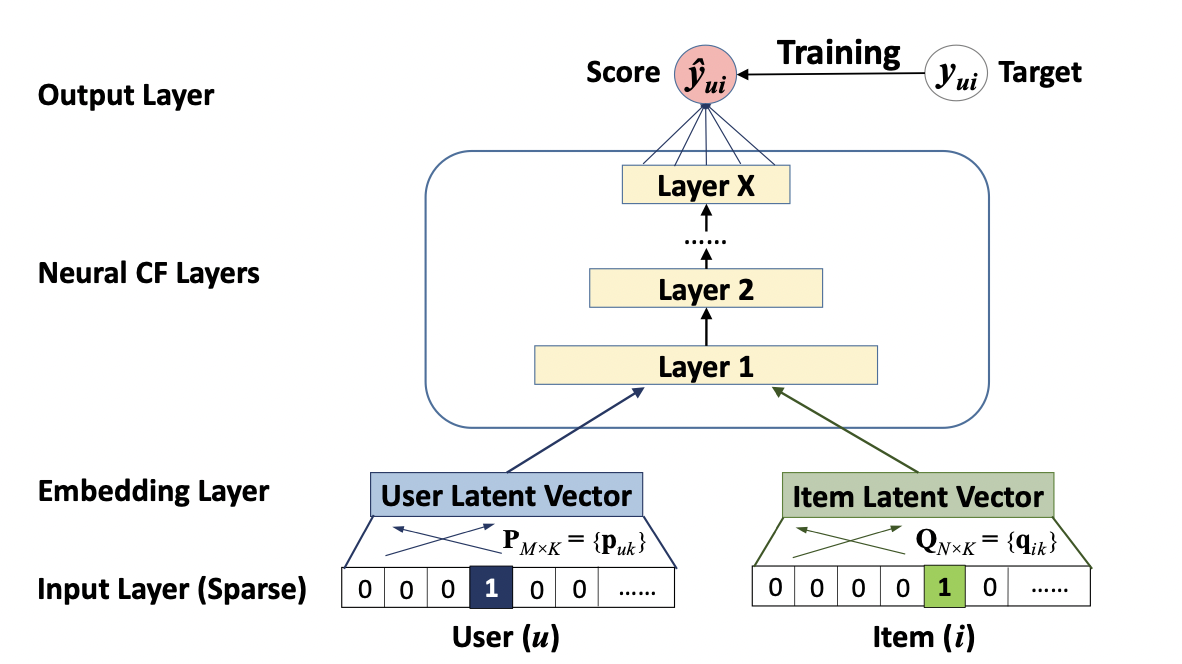
[출처] https://arxiv.org/pdf/1708.05031.pdf, Neural Collaborative Filtering
위에서의 신경망 MF에서는 단순히 Embedding Layer의 결과를 내적하는 연산을 취한다면, Neural MF에서 Multi Layer Perceptron 부분은 hidden layer를 여러 개 두어서 기존 MF보다 데이터에서 비선형적인 특징을 학습할 수 있는 장점을 지닌다.
MLP 부분 외의 NeuMF에 관한 자세한 내용은 다음 포스팅에서 확인할 수 있다.
https://glanceyes.tistory.com/entry/추천-시스템-딥러닝을-사용한-추천-시스템과-이를-응용한-유튜브-영상-추천-시스템
딥 러닝을 사용한 추천 시스템과 대표적인 예시인 유튜브 영상 추천
2022년 3월 7일(월)부터 11일(금)까지 네이버 부스트캠프(boostcamp) AI Tech 강의를 들으면서 개인적으로 중요하다고 생각되거나 짚고 넘어가야 할 핵심 내용들만 간단하게 메모한 내용입니다. 틀리거
glanceyes.tistory.com
'AI > 추천 시스템' 카테고리의 다른 글
| GNN(Graph Neural Network)의 정의와 특징 그리고 추천시스템에서의 GNN 계열 모델 (1) | 2023.01.02 |
|---|---|
| 추천 시스템의 평가 방법과 실험에서의 데이터 분할 전략 (0) | 2022.04.26 |
| Side Information과 이를 사용하는 추천 시스템 (1) | 2022.04.20 |
| Deep Learning 기반의 Collaborative Filtering (0) | 2022.04.18 |
| 추천 시스템에서의 Implicit Feedback (0) | 2022.04.18 |
소중한 공감 감사합니다.