Context 기반 추천 모델인 FM(Factorization Model)과 FFM(Field-aware Factorization Machine)

 

 

Context-aware Recommendation

 

행렬 분해 기법(MF)을 활용한 협업 필터링의 한계

 

개별 유저와 개별 아이템 간 상호작용을 2차원 행렬로 표현한다.

그러나 이는 유저의 데모그래픽이나 아이템의 카테고리 및 태그 등 여러 풍부한 특성(feature)들을 추천 시스템에 반영할 수 없다.

또한 유저-아이템의 상호작용 정보가 아직 부족할 경우, 즉 'cold start'에 대한 대처가 어렵다.

 

 

Context 기반 추천 시스템

 

유저와 아이템 간 상호작용 정보 뿐만이 아니라 맥락(context)적 정보도 함께 반영하는 추천 시스템이다.

$X$를 통해 $Y$의 값을 추론하는 일반적인 예측 문제에 두루 사용할 수 있는 General Predictor이다.

 

$$ R: User \times Item \times Context \rightarrow Rating $$

 

 

Click-Through Rate Prediction

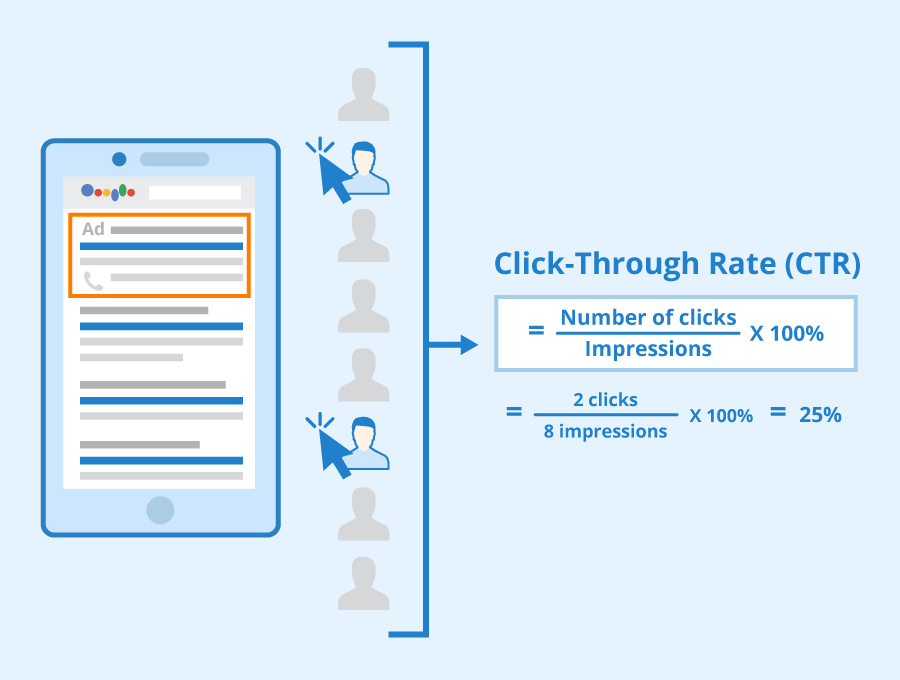
[출처] https://www.seobility.net/en/wiki/CTR_(Click-Through_Rate)

 

CTR 예측

 

유저가 주어진 아이템을 클릭할 확률(probability)을 예측하는 문제이다.

추천 시스템에서 온라인 A/B 테스트를 할 때 가장 많이 사용하는 평가 지표이다.

예측해야 하는 $y$값은 클릭 여부(0 또는 1)이므로 이진 분류(binary classification) 문제에 해당된다.

모델에서 출력한 실수 값을 시그모이드 함수에 통과시키면 (0, 1) 사이의 예측 CTR 값을 구할 수 있다.

 

CTR 예측은 광고에서 주로 사용되는데, 광고 추천을 잘 하면 이는 곧 돈이 되므로 매우 중요하다.

광고가 노출된 상황의 다양한 유저, 광고, context feature를 사용하여 예측할 수 있다.

유저 ID가 존재하지 않는 데이터도 다른 유저 feature나 context feature를 사용하여 예측할 수 있다.

 

 

Logistic Regression

 

기본 모형

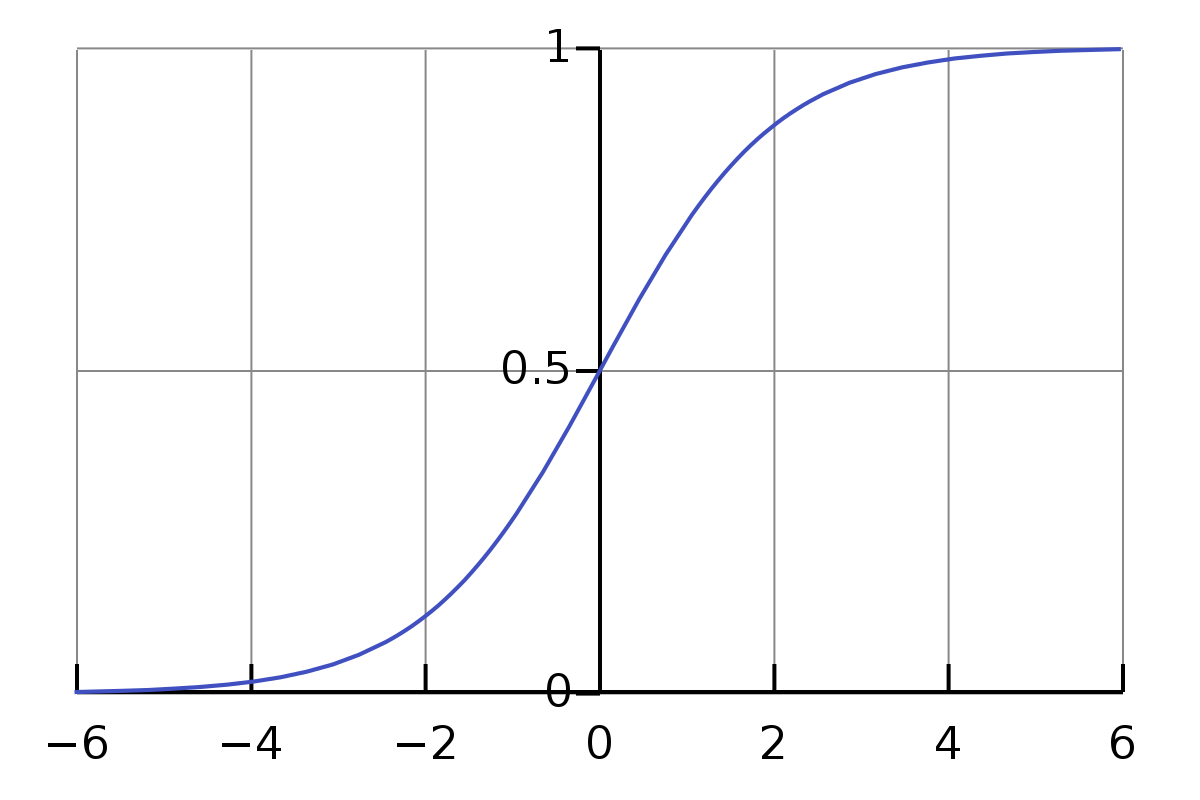
[출처] https://commons.wikimedia.org/wiki/File:Logistic-curve.svg, Qef

 

이진 분류 문제의 예측에서 주로 사용하는 함수이다.

기본적인 선형 모델에다가 시그모이드를 적용한 형태이다.

 

$$ logit(P(y=1|x) = \big{(}w_0 + \sum_{i=1}^n w_i x_i \big{)}, \quad w_i \in \mathbb{R} $$

 

유저, 아이템, context feature는 $x_i$라는 입력 변수로 사용된다.

그러나 변수 간의 상호작용을 모델링할 수는 없다.

 

 

Polynomial Model

 

변수 간의 상호작용을 고려해서 둘 이상의 변수를 cartisian product하여 $w_{ij}$라는 파라미터로 학습하는 모델이다.

예측 성능은 올라가지만, 파라미터 수가 급격히 증가하는 단점이 있다.

$$ logit(P(y=1|x) = \big{(}w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_{i} x_{j} \big{)}, \quad w_i, w_{ij} \in \mathbb{R} $$

 

 

 

사용 데이터

 

Dense Feature

벡터로 표현했을 때 비교적 작은 공간에 밀집되어 분포하는 수치형 변수이다.

 

Sparse Feature

벡터로 표현했을 때 비교적 넓은 공간에 분포하는 범주형 변수이다.

 

CTR 예측 문제에 사용되는 데이터를 구성하는 요소는 대부분 sparse feature이다.

그러나 모든 데이터를 one-hot encoding으로 표현하면 파라미터 수가 너무 많아질 수 있다.

또한 학습 데이터에 등장하는 빈도에 따라 특정 카테고리가 과적합 또는 과소적합될 수 있다.

 

 

그래서 feature embedding을 한 이후에 이 feature를 가지고 예측을 하기도 한다.

Item2Vec에서 아이템을 벡터로 나타내는 것도 feature embedding의 기법 중 하나이다.

또한 자연어 처리에 사용되는 LDA, BERT의 텍스트 임베딩 기법들도 흔히 적용된다.

 

 

 

Factorization Machine

 

 

SVM과 MF와 같은 Factorization Model의 장점을 결합한 모델이다.

 

 

Factorization Machine 등장 배경

 

딥러닝이 등장하기 이전에는 Support Vector Machine(SVM)이 가장 많이 사용되는 모델이었다.

커널 공간을 활용하여 비선형 데이터 셋에 관해서 높은 성능을 보였다.

 

그럼에도 불구하고 유저-아이템에 대한 평점을 예측하는 CF 환경에서는 SVM보다 MF 계열의 모델이 더 높은 성능을 내왔다.

매우 희소한 데이터에 관해서는 SVM이 좋은 성능을 내지 못한다.

 

 

하지만 MF 모델은 특별한 환경 또는 데이터에만 적용할 수 있다.

$X: (\text{user}, \text{item}) \rightarrow Y: (\text{rating})$으로 이루어진 데이터에 관해서만 적용이 가능하다.

 

SVM과 MF의 장점을 결합하고자 하는 시도에서 출발한 아이디어이다.

 

 

FM 공식

 

$$ \hat{y}(x) = \big{(}w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \big{<} v_i, v_j \big{>} x_{i} x_{j} \big{)}\\ w_i \in \mathbb{R},\quad x_i \in \mathbb{R}, \quad v_i \in \mathbb{R}^k $$

 

$x_i$와 $x_j$가 상호작용할 때, $x_i$에 해당되는 $v_i$, $x_j$에 해당되는 $v_j$인 $k$ 차원의 factorization 파라미터로 각각 곱해져서 두 feature 간의 상호작용을 모델링한다.

두 feature 간의 상호작용 term에서 Polynomial Model과 차이가 있음을 알 수 있다.

$$ \big{<} v_i, v_j \big{>} := \sum_{f=1}^k v_{i,f} \cdot v_{j, f} $$

여기서 $\big{<} v_i, v_j \big{>}$는 두 벡터의 스칼라 곱을 의미한다.

 

 

FM의 활용

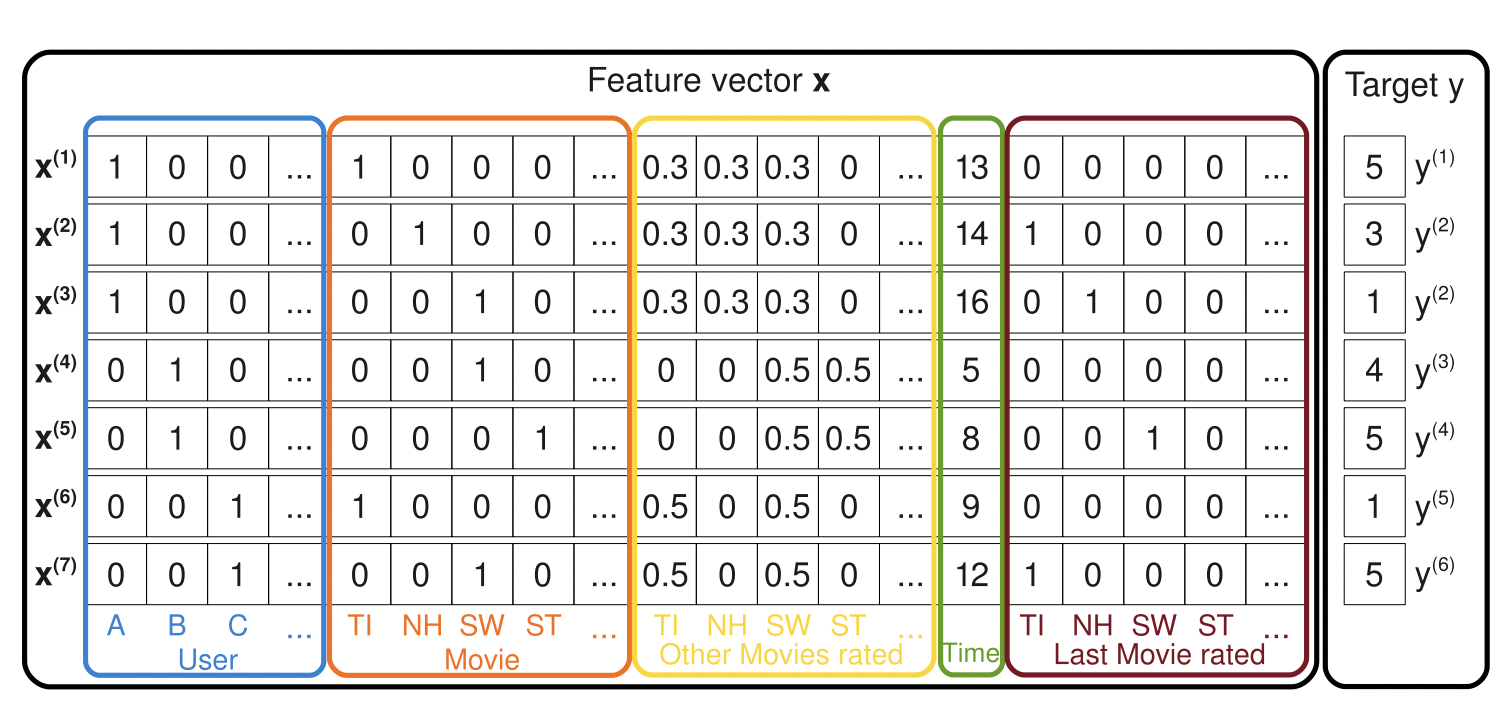
[출처], https://sdcast.ksdaemon.ru/wp-content/uploads/2020/02/Rendle2010FM.pdf, Factorization Machines

 

Sparse한 데이터 셋에서 예측하기

유저의 영화에 대한 평점 데이터는 대표적인 High Sparsity 데이터이며, 위의 이미지의 데이터를 예시로 들 수 있다.

영화에 대한 평점 데이터를 ${(u_1, m_2, 5), (u_3, m_1, 4), (u_2, m_3, 1), \cdots }$ 등 CF 문제의 입력 데이터로 나타낼 수 있다.

평점 데이터를 일반적인 입력 데이터로 바꾸면, 입력 값의 차원이 전체 유저와 아이템 수만큼 증가한다.

 

$(u_1, m_2, 5) \rightarrow [ \underbrace{1, 0, 0, \cdots, 0}_{\text{U}}, \underbrace{0, 1, 0, \cdots, 0}_{\text{M}}, 5]$

 

위의 이미지에서 나온 바와 같이 해당 논문에서 나온 예시를 좀 더 자세히 설명하면 다음과 같다.

저기서 앞의 4개의 파란색 컬럼에 나타난 것은 active user를 나타내는 indicator이며, 각 유저마다 unique한 값을 갖는다.

 

User A = $(1, 0, 0, \cdots)$

User B = $(0, 1, 0, \cdots)$

User C = $(0, 0, 1, \cdots)$

 

그 다음 5개의 주황색 컬럼은 active item을 의미하는 indicator이며, 각 유저별로 어떠한 영화에 평점을 매겼는지를 의미한다.

예를 들어, $\mathbf{x^{(4)}}$ 벡터에서 앞쪽 원소인 $(0, 1, 0, \cdots, 0, 0, 1, 0, \cdots), \cdots$의 의미는 유저 B가 영화 SW에 평점을 매겼다는 것을 뜻한다.

 

그 이후 노란색 컬럼은 해당 유저가 그동안 평점을 매긴 다른 영화가 무엇인지를 의미하고, 초록색 컬럼은 어떠한 달에 평점을 매겼는지를, 갈색 컬럼은 현재 평점을 매긴 active item외의 마지막으로 평점을 매긴 영화가 무엇인지를 뜻한다.

 

유저 A의 어떤 영화 ST에 관한 평점을 FM 모델을 통해 예측한다고 가정한다.

이때 $\mathrm{v}_A$, $\mathrm{v}_{ST}$가 FM 모델을 통해 학습되므로 상호작용이 반영된다.

 

$\mathrm{v}_{ST}$: 유저 B,C의 영화 ST에 대한 평점 데이터를 통해 학습된다. (여기서 유저 B, C는 영화 ST 외에 다른 영화(SW)도 평가했다.)

$\mathrm{v}_A$: 유저 B, C가 유저 A와 공유하는 영화 SW의 평점 데이터를 통해 학습된다. (영화 SW는 유저 A, B, C 모두 평가했다.)

 

ST라는 영화가 SW라는 영화에 비해서 상대적으로 어떤 특징을 지니는지가 $\mathrm{v}_{ST}$를 통해 학습된다.

유저 B, C와는 다른 또 다른 유저인 A의 상대적인 특징이 $\mathrm{v}_A$를 통해 학습된다.

 

 

 

FM의 장점

 

SVM와의 비교

 

FM는 SVM와는 달리 매우 sparse한 데이터에 관해서 높은 예측 성능을 보인다.

SVM와는 다르게 선형 복잡도($O(kn)$)를 가지므로 수십 억개 의 학습 데이터에 관해서도 빠르게 학습한다.

모델의 학습에 필요한 파라미터의 개수도 SVM와는 달리 선형적으로 비례하다.

 

 

Matrix Factorization와의 비교

 

MF와는 달리 여러 예측 문제에 모두 활용 가능한 범용적인 지도 학습 모델이다.

일반적인 실수 변수를 모델의 입력으로 사용할 수 있으며, MF와 비교할 때 유저, 아이템 ID 외에 다른 부가 정보들을 모델의 feature로 사용할 수 있다.

 

 

 

 

Field-aware Factorization Machine(FFM)

 

FM의 변형된 모델이며, 상대적으로 더 높은 성능을 보인 모델이다.

 

 

FFM 등장 배경

 

FM은 예측 문제에 두루 적용 가능한 모델로, 특히 sparse 데이터로 구성된 CTR 예측에서 좋은 성능을 보인다.

FFM은 FM을 발전시킨 모델로서 PITF(Pairwise Interacton Tensor Factorization) 모델에서 아이디어를 얻었다.

여기서 PITF는 MF를 발전시킨 모델이다.

PITF에서는 (user, item, tag) 3개의 필드에 대한 클릭률을 예측하기 위해 (user, item), (item, tag), (user, tag) 각각에 관해서 임베딩된 서로 다른 latent factor를 정의하여 구한다.

이를 일반화하여 여러 개의 필드에 관해 latent factor를 정의한 것이 FFM이다.

사용자가 원하는 만큼 필드의 수를 늘려서 상호작용을 임베딩할 수 있다.

 

 

FFM의 특징

 

입력 변수를 필드(field)로 나누어서 필드별로 서로 다른 latent factor를 가지도록 factorize한다.

기존의 FM은 하나의 변수에 관해서 $k$개로 factorize하지만, FFM은 $f$개의 필드에 관해 각각 $k$개로 factorize한다.

 

Field는 모델을 설계할 때 함께 정의하며, 같은 의미를 갖는 변수들의 집합으로 설정한다.

예를 들면, 다음과 같이 변수를 묶을 수 있다.

 

• 유저: 성별, 디바이스, 운영체제
• 아이템: 광고, 카테고리
• 컨텍스트: 어플리케이션, 배너

 

CTR 예측에 사용되는 feature는 이보다 훨씬 다양한데, feature의 개수만큼 필드를 정의하여 사용할 수 있다.

 

 

FFM의 공식

 

$$ \hat{y}(x) = \big{(}w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \big{<} v_{i, f_{j}}, v_{j, f_{i}} \big{>} x_{i} x_{j} \big{)}\\ w_i \in \mathbb{R},\quad w_i \in \mathbb{R}, \quad v_{i, f} \in \mathbb{R}^k $$

 

FM과 FFM의 차이를 간단히 정리하기 위해 예시를 들어 설명할 수 있다.

다음과 같이 광고 클릭 데이터가 존재하고, 사용할 수 있는 feature가 총 세 개(Publisher, Advertiser, Gender)라고 가정한다.

Clicked	Publisher	Advertiser	Gender
Yes	ESPN	Nike	Male

 

FM에서는 필드라는 게 존재하지 않고, 하나의 변수에 관해 factorization 차원인 $k$만큼의 파라미터를 학습해야 한다.

그래서 벡터 $\mathbf{x}$에 대한 평점 예측의 식을 다음과 같이 정의할 수 있다.

 

 

$$ \hat{y}(\mathbf{x}) = w_0 + w_{\text{ESPN}} + w_{\text{Nike}} + w_{\text{Male}} + v_{\text{ESPN}} \cdot v_{\text{Nike}} + v_{\text{ESPN}} \cdot v_{\text{Male}} + v_{\text{Nike}} \cdot v_{\text{Male}} $$

 

 

FFM에서는 각각의 feature에 관한 필드를 P, A, G로 정의할 수 있다.

FFM을 사용할 때는 하나의 변수에 관해서 필드 개수 $f$와 factorization 차원인 $k$의 곱인 $fk$만큼의 파라미터를 학습해야 한다.

 

 

$$ \hat{y}(\mathbf{x}) = w_0 + w_{\text{ESPN}} + w_{\text{Nike}} + w_{\text{Male}} + v_{\text{ESPN, A}} \cdot v_{\text{Nike, P}} + v_{\text{ESPN, G}} \cdot v_{\text{Male, P}} + v_{\text{Nike, G}} \cdot v_{\text{Male, A}} $$

 

 

 

FFM의 활용

 

마찬가지로 다음과 같이 광고 클릭 데이터가 존재하고, 사용할 수 있는 feature가 총 세 개(Publisher, Advertiser, Gender)라고 가정한다.

Clicked	Publisher	Advertiser	Gender
Yes	ESPN	Nike	Male

 

 

Categorical Feature

 

같은 feature 그룹을 같은 field로 묶어서 정의한다.

광고 예시를 들면 다음과 같이 필드를 정의할 수 있다.

 

Clicked	Publisher	Advertiser	Gender
Yes	P:P-ESPN:1	A:A-Nike:1	G:G-Male:1

 

 

Numerical Feature

 

다음과 같이 Numerical Value를 갖는 데이터가 존재한다고 가정한다.

 

Accepted	AR	Hidx	Cite
Yes	45.73	2	3

 

 

Dummy Field 사용

 

Numeric feature 한 개당 하나의 필드에 할당하고 실수 값을 사용한다.

 

Accepted	AR	Hidx	Cite
Yes	AR:AR:45.73	Hidx:Hidx:2	Cite:Cite:3

 

 

Dicretize

 

Numeric feature를 $n$개의 구간으로 나누어 이진 값을 사용하고, $n$개의 변수를 하나의 필드에 할당한다.

다음은 정수 구간으로 나눠서 각각의 변수를 필드에 할당한 예시이다.

 

Accepted	AR	Hidx	Cite
Yes	AR:45:1	Hidx:2:1	Cite:3:1