Transformer의 Multi-Head Attention과 Transformer에서 쓰인 다양한 기법
- -
앞서 우리는 입력으로 주어진 sequence에서 어떠한 부분에 주목할지를 예측에 반영하는 attention 기법을 배웠다. 이러한 Self-Attention에서 좀 더 나아가 head를 여러 개 사용하여 주어진 데이터를 이해하려는 Multi-Head Attention 기법과 이외 'Attention is All You Need' 논문에서 소개되었던 다른 기법들도 이해해 보고자 한다. 이전의 transformer에 관해 다룬 포스트의 내용을 기반으로 하므로 아래의 글을 참조하면 이 글을 이해하는 데 도움이 될 수 있다.
Self-Attention을 사용하는 Transformer
Self-Attention을 사용하는 Transformer(트랜스포머)
Sequential Model Sequential Model이 어려운 이유 언어 문장을 예로 들면 완벽한 문장 구조에 대응되도록 문장을 만드는 경우는 흔치 않은데, 이러한 문제는 sequential model에 있어서 난관이다. 또한 기존 Se
glanceyes.com
Transformer의 Self-Attention과 Seq2Seq with Attention 모델과의 비교
Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교
Transformer를 이해하려면 Seq2Seq with Attention 모델이 나오게 된 배경과 그 방법을 이해하는 것이 필요하다. 특히 transformer의 self-attention에 관해 한줄로 요약하면, Seq2Seq with Attention에서 decoder의 hidden st
glanceyes.com
그림으로 정리하는 Transformer
Transformer에서 얻어갈 내용은 꽤 많다고 생각한다. 그러나 그 내용을 하나하나씩 보면 파편화 되어 있는 듯한 느낌이 들어서 이를 한번 종합하여 정리해 보는 시간이 필요해 보인다. 각 부분에 대한 설명은 그 부분을 칠한 형광펜의 색을 달리하여 따로 정리했다.
Transformer의 전체 구조

Self-Attention

Self-Attention에 관한 자세한 내용은 아래 글을 참조.
Transformer의 Self-Attention과 Seq2Seq with Attention 모델과의 비교
Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교
Transformer를 이해하려면 Seq2Seq with Attention 모델이 나오게 된 배경과 그 방법을 이해하는 것이 필요하다. 특히 transformer의 self-attention에 관해 한줄로 요약하면, Seq2Seq with Attention에서 decoder의 hidden st
glanceyes.com
Transformer의 Multi-Head Attention(MHA)

Multi-Head Attention(MHA)이란?
앞서 공부한 Self-Attention을 정리하면 Attention 모듈에서 query, key, value vector로 만들 입력을 주고, 각 종류의 벡터에 관해 파라미터인 $W_Q$, $W_K,$ $W_V$를 가지고 선형 변환을 통해 query, key, value vector를 생성한다.
이후 보고자 하는 단어에 관한 query vector와 모든 단어에 관한 key vector 간의 내적을 통해 반영 가중치인 attention score를 구하고, 이를 통해 value vector의 가중 평균을 구하여 최종적인 output인 단어의 encoding vector를 생성한다.
Multi-Head Attention은 각각의 동일한 query, key, value vector에 관해 동시에 병렬적으로 attention을 구하는 방법이며, 앞서 설명한 Scaled Dot-Product Attention을 여러 개의 head로 나누어 수행하는 것이다.
Query, key, value vector로 만들 입력은 동일하게 주어지지만, 이를 query, key, value vector로 선형 변환할 때 사용하는 파라미터인 $W_Q$, $W_K$, $W_V$를 각 head 별로 서로 다르게 만들어 학습한다.
예를 들어, $i$번째 head에서 query, key, value vector를 생성할 때 사용하는 파라미터는 $W_i^Q$, $W_i^K$, $W_i^V$가 될 것이다.
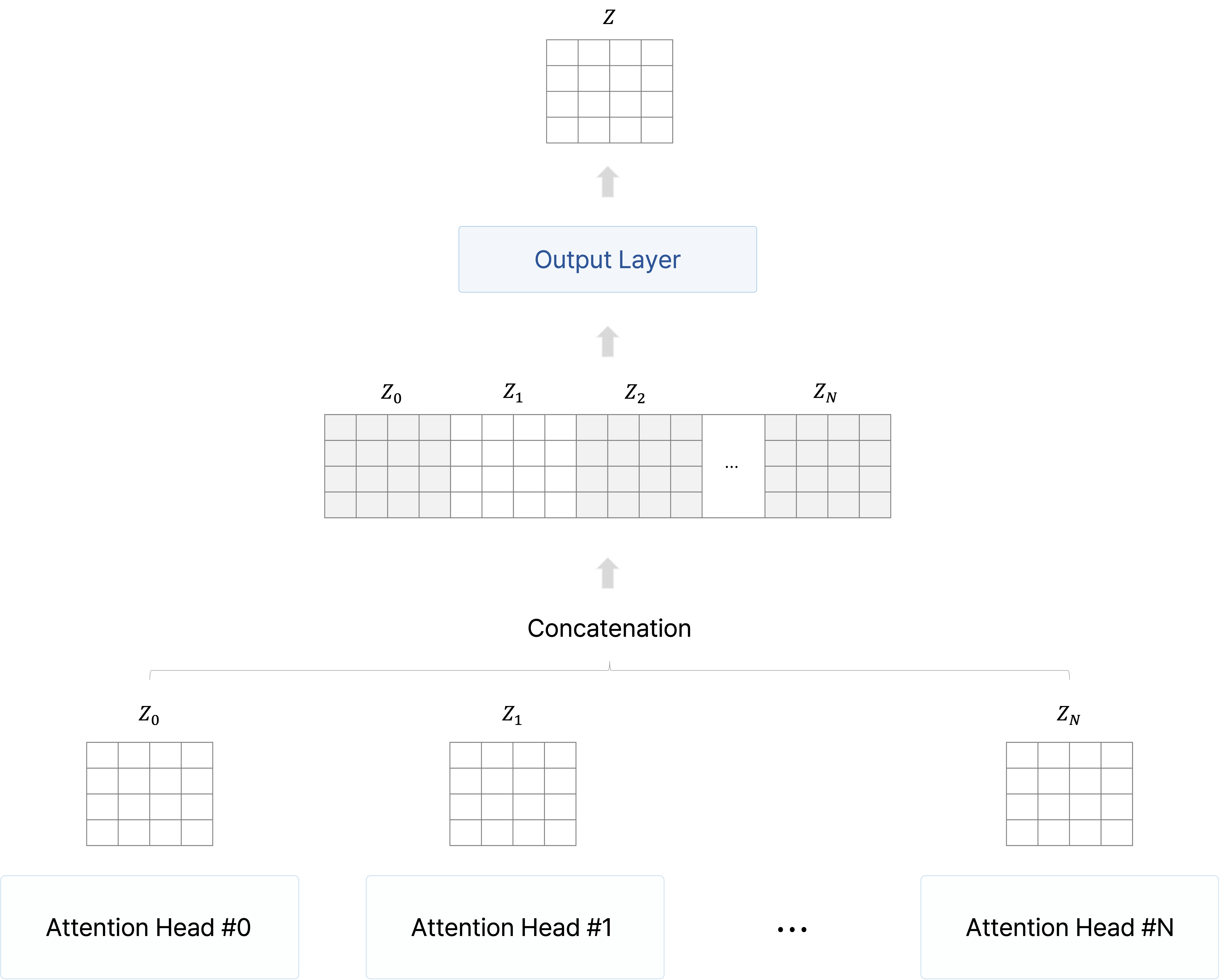
서로 다른 attention의 수만큼 동일한 단어에 대한 서로 다른 encoding vector $Z_i$가 생성되고, 이를 concatenation하고 $W^O$ 파라미터를 통해 선형 변환을 거쳐 해당 단어에 관한 최종적인 encoding vector를 얻는다.
위의 그림에서는 정확히 표현되지 않았으나 'Attention is All You Need' 논문에서는 각 단어의 임베딩 벡터의 차원을 512로 하고 8개의 attention head를 사용했는데, 주목할 점은 query, key, value 행렬인 $Q_i$, $K_i$, $V_i$의 각 행 벡터의 차원 크기가 512를 8로 나눈 64를 갖도록 했다.
원래 임베딩 벡터 차원 그대로 가져가지 않고 각 단어의 임베딩 벡터를 head의 수로 나눈 차원으로 변환하는 이유는 multi-head attention을 병렬적으로 수행할 때 필요한 파라미터 수를 줄이면서 결과적으로 다양한 정보를 파악하기 위함으로 해석할 수 있다.
마치 앙상블에서 약한 학습 결과를 모아 더 좋은 성능의 학습 결과를 도출하는 것과 비슷한 맥락으로 개인적으로 이해했다.
주의할 건 multi-head attention의 목적이 input 자체를 작은 차원의 여러 개로 나눠서 query, key, value vector로 만드는 게 아니다. 이 논문에서 512 차원의 input을 64 차원으로 줄인다고 하는 부분에서 헷갈리지 말아야 할 점이 input으로부터 query, key, value vector를 만드는 변환 행렬인 $W_i^Q$, $W_i^K$, $W_i^V$의 output 차원을 줄여서 그 query, key, value에 관해 self-attention을 수행하는 게 핵심이다. 즉, input을 여러 개의 작은 차원으로 slice 하는 게 아니라 query, key, value를 좀 더 작은 차원에서 수행하는데 이를 서로 다른 변환 행렬에 관해 구한 attention 결과를 concatenate 한 것이다.
Multi-Head Attention을 사용하는 이유
어떤 동일한 sequence가 주어졌을 때도 특정한 query word에 관해 서로 다른 기준으로 여러 관점에서의 정보를 뽑아와야 할 필요성이 있다. 예를 들어, 문장에서 어떤 주어가 되는 대상이 한 행동 중심의 정보를 뽑아와야 할 뿐더러, 주체가 있는 장소에 관한 정보도 뽑아 올 필요가 있다.
그런데 기존의 One-Head Attention 기법은 어떤 한 단어가 다른 단어와 상호작용하는 정보를 한 가지 방법으로 뽑아올 수 밖에 없다. 그래서 head를 여러 개 두어서 좀 더 다양한 관점에서의 정보를 얻는 과정을 병렬적으로 수행하고자 하는 목적에서 Multi-Head Attention이 사용된다.
Multi-Head Attention 학습 과정
예를 들어, 두 단어 $x_1$, $x_2$로 이루어진 sequence를 입력으로 사용하여 8개의 head를 지닌 attention의 학습 과정을 살펴보면 다음과 같다.
단어 $x_1$, $x_2$가 각각 한 행을 이루는 입력 벡터에 관한 행렬 $X$를 $i$번째 head에서 $W_i^K$, $W_i^K,$ $W_i^V$ 파라미터를 사용하여 $Q_i$, $K_i$, $V_i$를 생성한다.
이를 가지고 각 head에 관해서 Scaling Dot-Product Attention을 수행하여 나온 결과인 encoding vector를 $Z_0$부터 $Z_7$까지 얻을 수 있다.
$Z_i$에서 각 행 벡터의 차원이 3차원이라고 할 때, 8개의 encoding vector 행렬을 모두 concatenation하면 한 행의 차원이 24인 행렬이 나온다.
이를 결과적으로 원하는 차원의 벡터로 변환하고자 $W^O$ 파라미터를 곱하는 선형 변환 output layer를 통해 최종 encoding vector 행렬인 $Z$를 구한다.
아래에서도 설명하겠지만, 일반적으로 skip connection을 수행하기 위해 multi-head attention으로 들어오는 입력인 단어에 관한 임베딩 벡터의 차원에 맞게 변환한다.
다른 모델과의 Complexity 비교

[출처] https://arxiv.org/pdf/1706.03762.pdf, Attention is All You Need
길이가 $n$인 sequence가 주어지고, query, key, value vector의 차원인 dimenstion of representation을 $d$라고 하자.
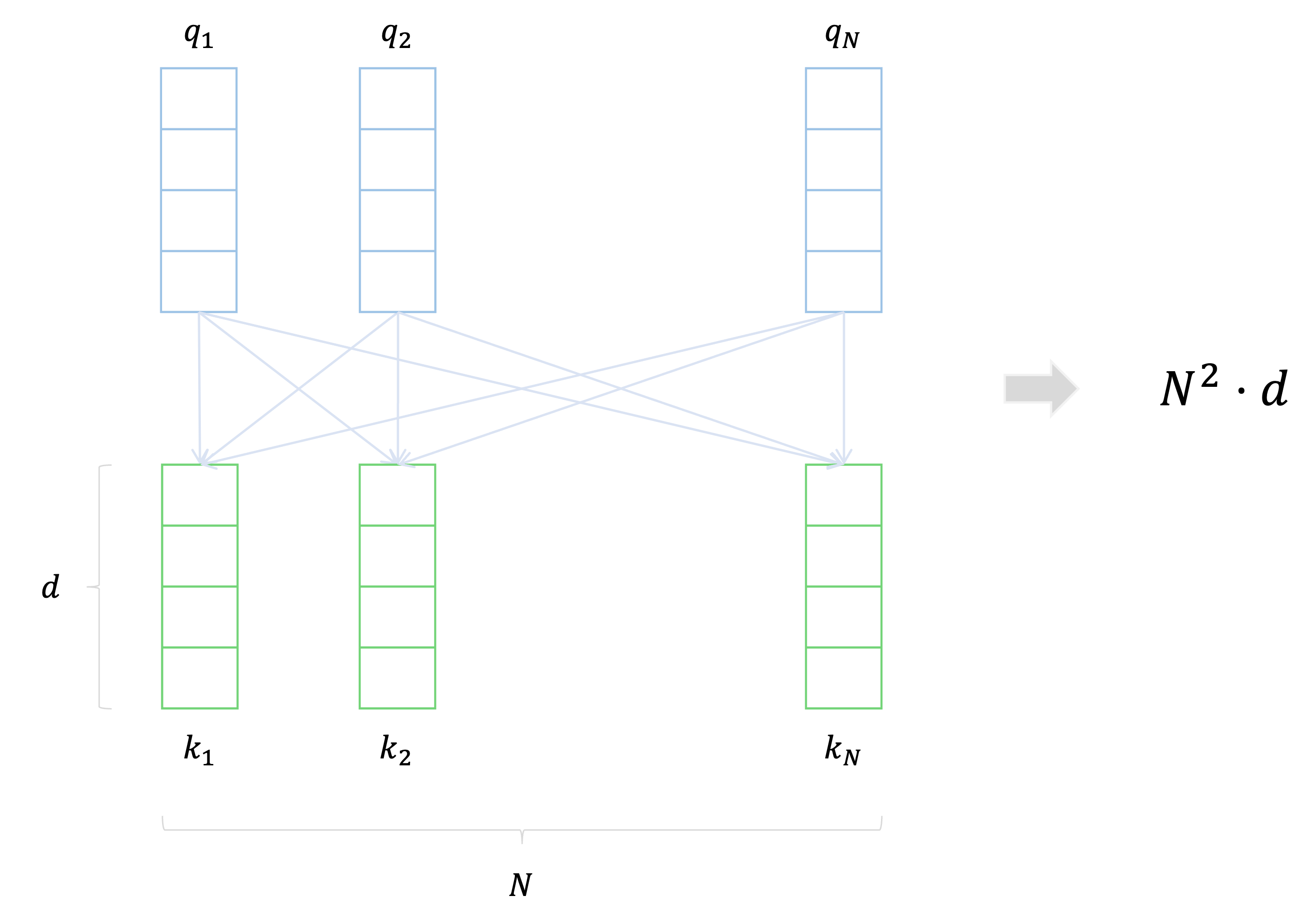
Self-Atttention에서 주된 연산 부분은 $\text{softmax}(\frac{QK^T}{\sqrt{d}})V$에서 각 단어별로 반영 가중치를 구하고자 attention score를 계산하는 $QK^T$ 부분이다.
이 과정에서 모든 각각의 query vector에 관해 $d$ 차원을 갖는 모든 key vector와의 내적을 구하므로, $n^2$개의 모든 단어 쌍에 관해 $d$개의 원소끼리 서로 곱해서 더하는 element-wise product를 수행한다.
그러므로 한 레이어에서의 complexity는 $O(n^2 \cdot d)$이 되지만, GPU 코어 수가 많으면 이러한 행렬 연산은 길이 $n$과 차원의 크기인 $d$가 크다 하더라도 병렬적으로 한 번에 수행할 수 있다.
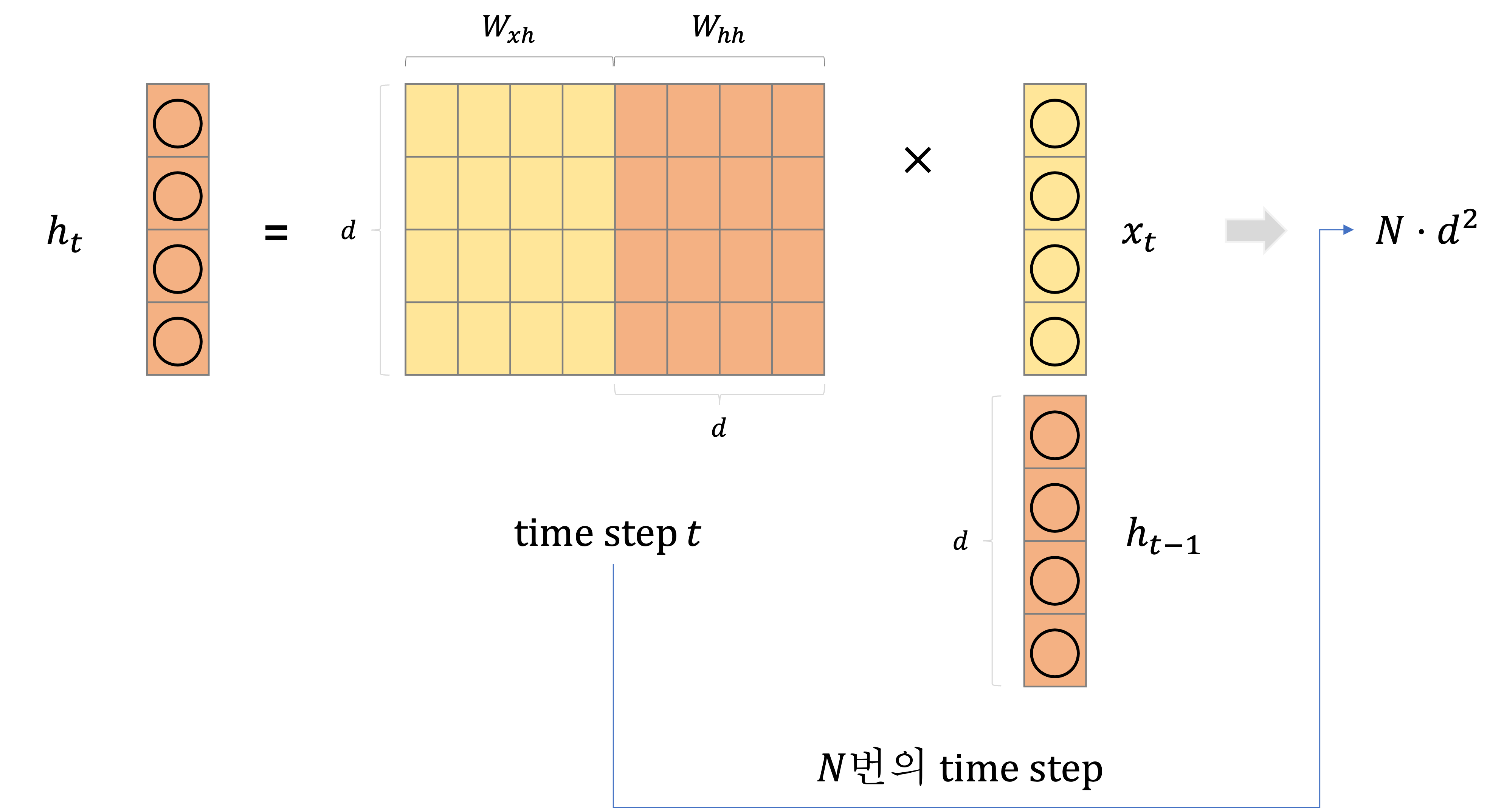
그러나 RNN에서는 주로 필요로 하는 연산은 매 time step마다 이전 time step의 hidden state인 $h_{t-1}$를 가지고 현재 hidden state인 $h_t$를 구해야 한다.
RNN에서 hidden state vector의 차원이 $d$라고 하고, 내보낼 현재 hidden state를 구하는 과정에서 input vector $x$의 차원은 상수로 고려한다고 가정하자. 그러면 연산에서 가장 주된 부분은 파라미터에서 $W_{hh}$와 $h_{t-1}$를 곱하여 $h_t$를 구하는 선형 변환이 일어나는 부분이다. 행렬 곱 연산에서 행마다 $d$개의 원소를 가지고 내적을 하므로 $O(d)$가 들고, 이를 $d$ 개의 모든 행에 관해 수행하므로 한 time step마다 $O(d^2)$만큼의 복잡도가 든다. 이러한 행렬 곱 연산을 모든 $n$번의 time step에 관해 수행하므로 최종적으로 $O(n \cdot d^2)$만큼의 복잡도가 든다.
결국 RNN에서는 이전 time step에서의 hidden state를 참고해야 되어서 모든 time step 계산을 순차적으로 수행해야 하므로 GPU의 코어 수가 어떻든 간에 병렬화 관점에서는 $O(n)$만큼의 복잡도가 들 수밖에 없다.
RNN에서 hidden state의 차원이자 Self-Attention에서 query, key, value vector의 차원인 $d$는 우리가 임의로 설정할 수 있지만, 입력으로 주어지는 sequence의 길이인 $n$은 우리가 원하지 않더라도 큰 값으로 올 수도 있으므로 $d$와는 달리 가변적인 값이 된다. 그래서 입력의 길이가 가변적인 점을 고려할 때 Transformer에서는 $O(n^2)$만큼의 메모리가 필요하지만, RNN에서는 $O(n)$만큼의 메모리가 필요하다. 그러므로 Self-Attention에서는 일반적으로 RNN보다 더 많은 메모리 양을 요구하는데, 이는 back propagation을 위해 모든 query와 key vector 간의 내적 값을 메모리에 저장하고 있어야 하기 때문이다.
종합하면 Self-Attention 기반의 transformer는 학습 속도면에서는 RNN보다 빠를 수 있지만, 일반적으로 RNN보다 더 많은 메모리 양을 요구하게 된다.
Multi-Head Attention은 좀 더 다양한 관점에서 데이터를 해석하자는 아이디어에서 출발
각 head별로 query, key, value vector에 관한 self-attention 수행
시간복잡도$O(n^2 \cdot d)$, 공간복잡도 $O(n^2)$으로 GPU 사용 시 병렬 처리로 학습 속도는 빠를 수 있어도 상대적으로 더 많은 메모리 사용량 요구
Transformer에서 쓰이는 다양한 기법
Block-Based Model
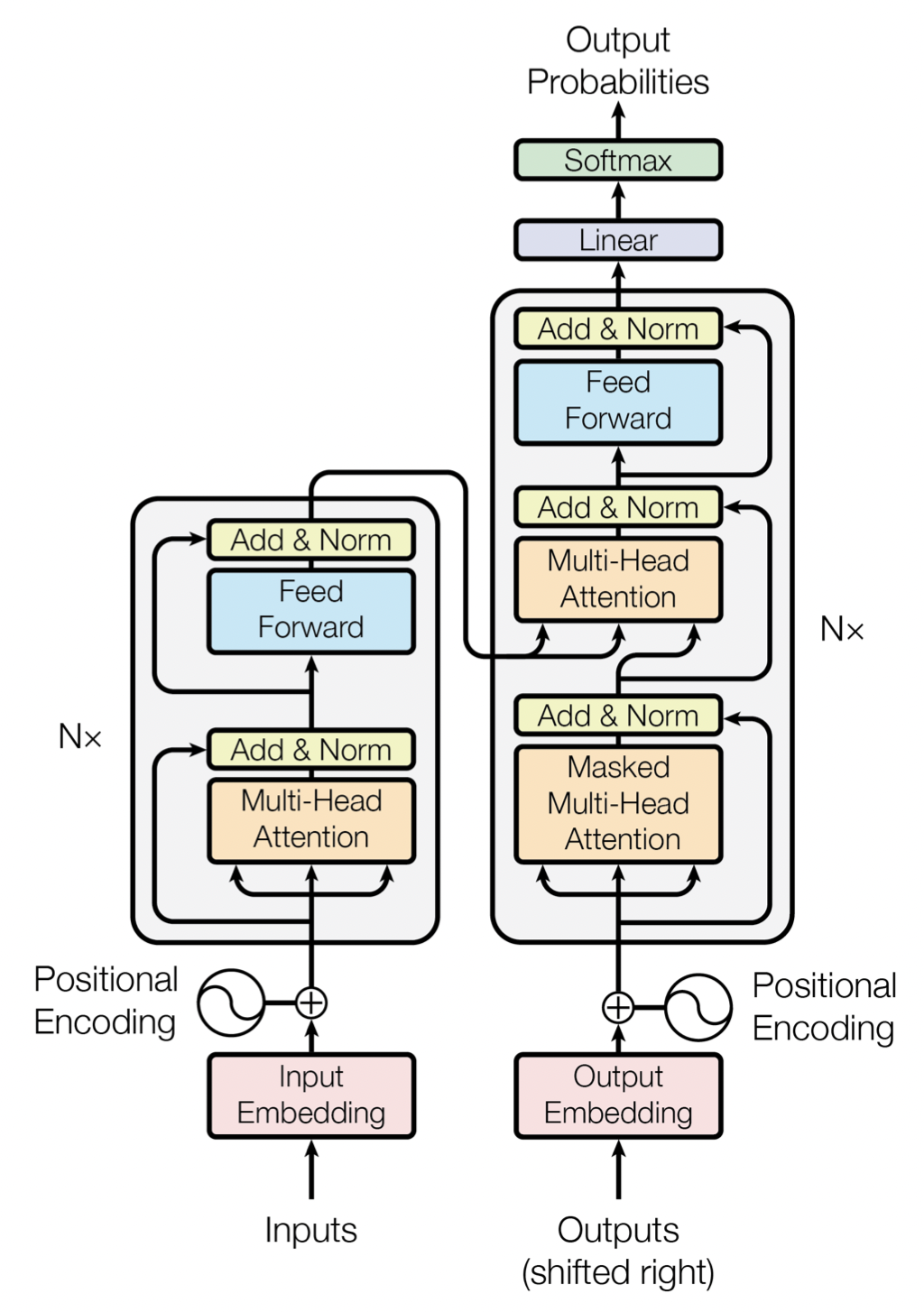
[출처] https://arxiv.org/pdf/1706.03762.pdf, Attention is All You Need
"Attention is All You Need" 논문에서 제시된 Transformer에서는 Multi-Head Attention을 핵심 모듈로 하고, 이에 더하여 여러 후처리를 진행하는 과정을 추가하여 하나의 모듈을 구성하게 된다.
Residual Connection

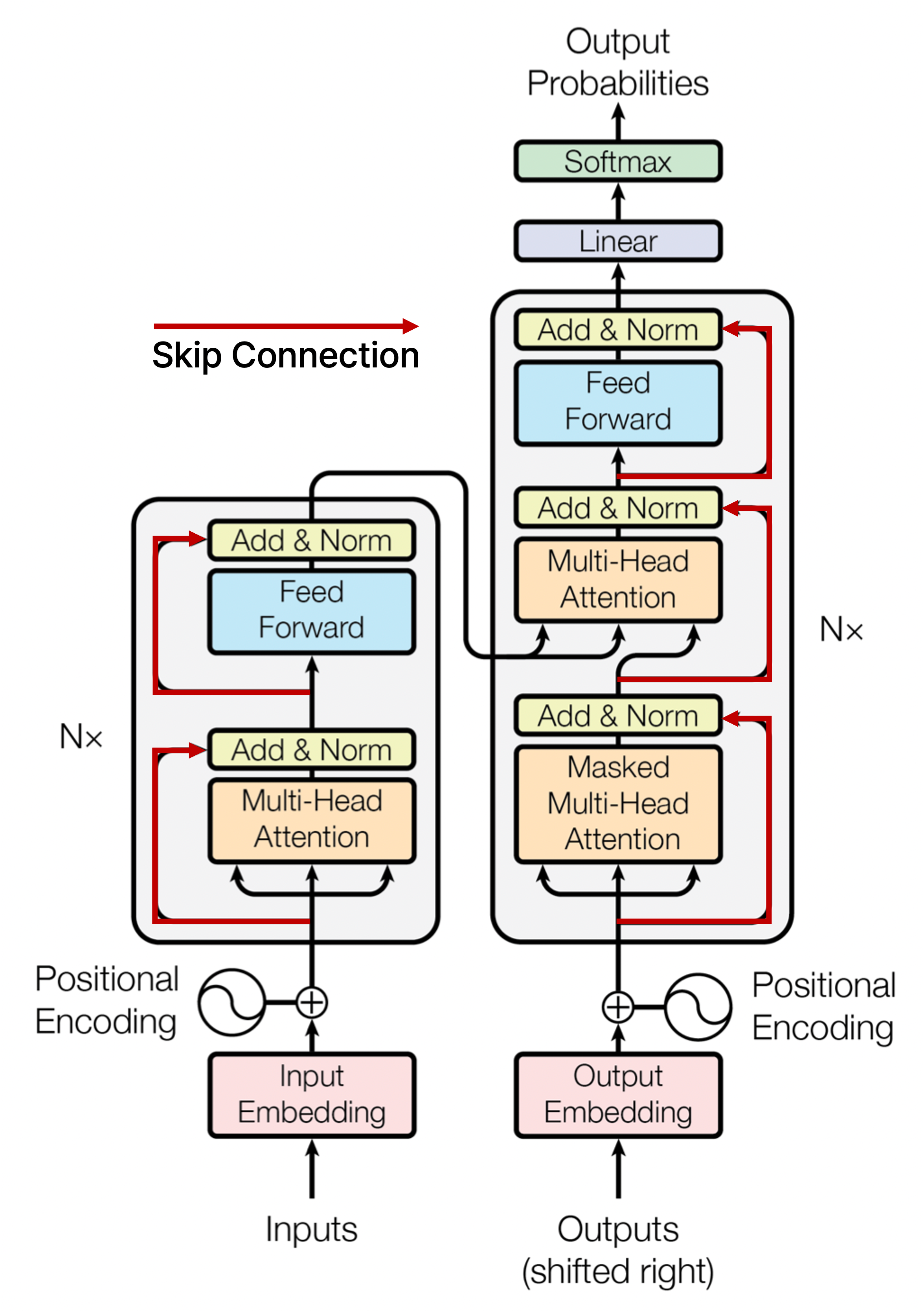
Residual connection은 computer vision에서 깊은 layer의 신경망을 만들 때 gradient vanishing 문제를 해결하여 학습을 안정화하고 동시에 더 깊은 layer를 쌓아도 좋은 성능을 낼 수 있도록 제안된 기법이다.
이 논문에서의 Transformer에서는 skip connection이라고도 불리는 residual connection을 적용하여 입력으로 Multi-Head Attention 모듈의 출력과 더한 후 layer normalization을 수행하며, 마찬가지로 feed forward network를 통과하면서 residual connection을 적용한다.
Residual connection을 사용할 때 주의할 점은 입력으로 주어지는 embedding vector의 차원과 모듈 또는 신경망을 통과하여 나오는 출력 vector의 차원이 동일해야 한다는 것이다.
그래서 Multi-Head Attention에서 각 head의 단어별 벡터를 concatenation하여 $W^O$를 가지고 선형 변환하는 output layer는 최종 encoding vector의 차원을 입력 차원과 같게끔 변환하는 역할을 한다.
Layer Normalization

딥 러닝에서는 batch norm, layer norm, instance norm, group norm 등 다양한 normalization 기법이 존재한다. 기본적으로 여러 normalization 기법은 주어진 다수의 sample에 관해 평균이 0이고 분산이 1인 분포로 만들어준 후, 우리가 원하는 평균과 분산을 주입할 수 있도록 만드는 선형변환을 행한다.
Layer Normalization

Layer normalization은 batch에 속하는 각 instance에 관한 feature의 평균과 분산을 구하여 그 feature 자체를 정규화 하는 과정이다.
앞서 설명한 batch normalization과 유사하게 layer normalization에서도 첫 번째 단계에서는 주어진 샘플에 관한 평균과 분산을 0과 1로 만들고, 원하는 평균과 분산을 주입하는 과정을 거친다.
$n$: feature vector의 크기 (원소 개수)
$\mu_i$: $i$번째 instance의 모든 feature vector 원소에 관한 평균
$\sigma_j^2$: $i$번째 instance의 모든 feature vector 원소에 관한 분산
$\hat{x}_{ij}$: $i$번째 instance의 feature vector의 $j$번째 원소에 관하여 표준화한 결과
어떤 학습 데이터가 단어라고 가정해보자. 그러면 batch sample로 볼 수 있는 각 단어에 대응되는 vector별로 normalization을 할 때, 각 단어의 feature인 vector의 원소에서 그 vector별 평균을 빼주고 표준편차를 나누는 과정을 수행한다. 이후 정규화한 vector에 원하는 평균과 분산을 주입하고자 affine transformation을 수행하는데, $ax + b$에서 파라미터에 해당하는 $a$, $b$를 한 set로 묶어서 각 노드별로 여러 단어에 걸쳐 공통적인 변환을 거치게 한다.
즉, 어떤 layer에서 발견되는 한 instance에 관한 feature vector에 관하여 그 feature vector 원소별로 동일한 변환을 수행하게 된다. Layer normalization도 batch normalization과 마찬가지로 학습 과정을 안정화하고 최종적인 성능을 끌어올리는 데 도움을 준다고 알려져 있다.
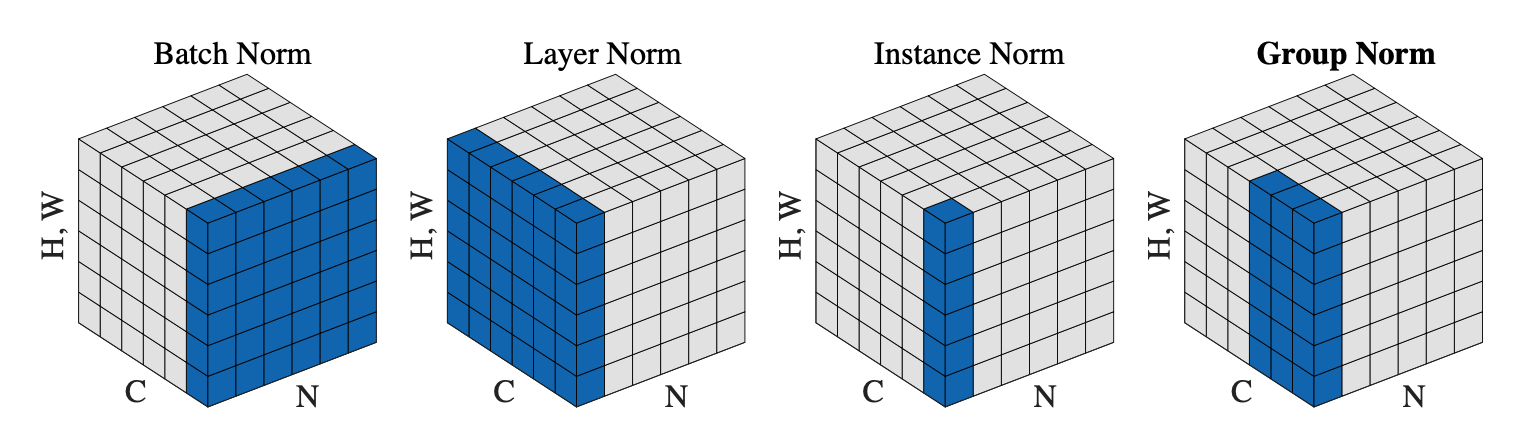
위에서는 각 instance의 feature의 channel이 1일 때로 가정했지만, channel이 1보다 클 때의 layer normalization을 정리하면 다음과 같다.
- Layer normalization: 하나의 instance의 feature에 관해 모든 channel에 대하여 해당 instance feature vector 그 자체에 정규화를 수행하는 것
Positional Encoding
RNN과는 달리 Transformer는 주어진 sequence를 self-attention으로 각 단어별 인코딩 벡터를 구할 때, 입력 sequence의 순서가 원래 순서와 달라져도 동일한 결과가 나올 것이다. 이는 각 단어별로 query vector를 모든 단어에 관한 key vector와 내적하여 유사도를 구할 때 모든 단어 쌍의 집합에 관해 확인할 뿐 실제 sequence에서의 순서는 고려하지 않아서다.
이러한 한계를 보완하고자 Positional Encoding을 사용하는데, 예시로는 매 위치마다 서로 다른 원소마다 unique한 값을 갖는 벡터를 만들어서 입력 벡터에 더하는 방법이 있다.
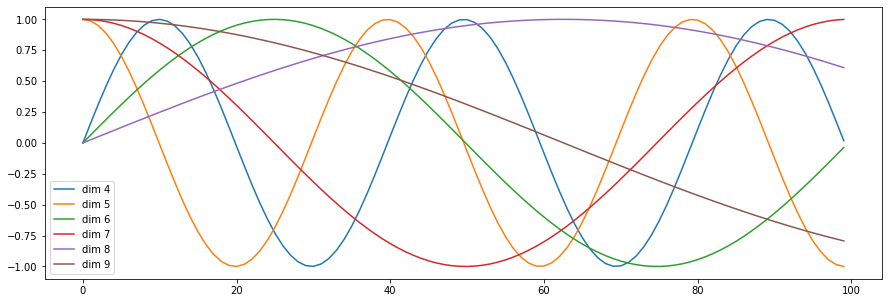
[출처] http://nlp.seas.harvard.edu/2018/04/03/attention, harvardnlp
일반적으로 위치에 따라 구별할 수 있는 벡터를 만들고자 $\sin$과 $\cos$을 사용하는데, 위치마다 서로 다른 $\sin$ 또는 $\cos$ 주기를 만든다.
위의 수식을 사용한 positional encoding에 의하면 단어의 위치에 관한 정보인 $pos$ 값에 따라 짝수 번째 차원의 원소는 $\sin$을, 홀수 번째 차원의 원소는 $\cos$ 그래프에서 대응되는 값을 갖도록 하여 이 원소를 하나로 모은 벡터를 입력 벡터에 더해주는 방식으로 적용할 수 있다.
왜 Sinusoidal 함수를 사용했는가?
Positional encoding의 목적은 입력의 각 token의 상대적인 위치를 구별할 수 있도록 하는 데 있다. 이를 위한 가장 간단한 방법은 위치가 뒤로 가면서 positional encoding의 원소 값이 커지게끔 하는 것이다. 그런데 이 방법의 문제는 입력의 길이는 가변적이고, 길이가 너무 길면 뒤의 원소에 관한 positional encoding의 원소 값이 매우 커지게 된다.
이의 대안으로 입력 길이에 관한 상대적인 위치를 positional encoding 원소 값으로 주는 것이다. 그렇지만 유사한 context의 input이 들어오더라도 input의 길이에 따라 상대 위치가 달라진다는 문제점이 존재한다. 만약 예를 들어 "엔간히 독한 마음"과 "엔간히 독한 마음 아니면 넌 시작하지마 이 일"의 두 문장에서 '마음'에 해당되는 token의 절대적인 위치는 세 번째로 동일하지만, 상대적인 위치는 후자에서 더 낮은 값을 지닐 것이다. 그래서 앞선 방법을 제외하고 절대 위치로 positional encoding 하는 방법이 필요하다.
또 다른 방법은 bit representation으로 poisitional encoding 하는 것이다. 예를 들어, 입력 길이가 16이고 4개의 비트를 사용하여 positional encoding을 하면 첫 번째 단어는 '1 0 0 0', 두 번째는 '0 1 0 0', 그 이후로는 '1 1 0 0', '0 0 1 0', '1 0 1 0'처럼 될 것이다. 그렇지만 입력의 길이를 예상하여 bit의 수를 정해야 한다는 단점이 있고, 또 그렇다고 input의 다양한 길이를 수용하기 위해 너무 많은 bit로 positional encoding을 하면 낭비되는 bit가 많다는 문제가 있다.
이러한 관점에서 sinusoidal positional encoding이 가장 좋은 방법이라고 볼 수 있다. 그 이유를 요약하면 다음과 같다.
(1) Positional encoding의 원소 값이 -1에서 1 사이의 값을 지니게 할 수 있다.
(2) 주기 함수의 frequency를 다양하게 줌으로써 임의의 두 위치에 관하여 그 positional encoding 결과가 겹칠 확률이 낮다.
왜 Sine과 Cosine이 Positional Encoding 원소에 번갈아 나타나는가?
$$ \begin{align} PE_{(pos, 2i)} &= \sin (pos / 10000^{2i/d_{\text{model}}})\\ PE_{(pos, 2i + 1)} &= \cos (pos / 10000^{2i/d_{\text{model}}}) \end{align} $$
이 논문에서 제안된 positional encoding을 유심히 살펴보면, sine 함수와 cosine 함수가 번갈아 나타난다는 사실을 확인할 수 있다. 주기함수를 아무 거나 사용해도 될 것 같이 보이는데 왜 굳이 sine으로만 혹은 cosine으로만 encoding 하지 않고 위치가 홀수인지 또는 짝수인지에 따라 번갈아 나타나게 한 이유가 궁금할 수 있다.
이는 어느 정도 의도한 부분이라고 볼 수 있는데, 만약 임의의 두 positional encoding를 dot product 할 때 그 상대적인 위치의 차이에만 영향을 받도록 하기 위해서다. 즉, 같은 위치의 positional encoding을 내적하면 그 similarity가 최대가 되도록 하고 싶은 것이다. 그렇게 해야 각 token의 위치에 관한 상대적인 정보를 제대로 encoding 했다고 볼 수 있어서다.
아래는 이처럼 positional encoding을 수행했을 때 임의의 위치 $i$에 관해 positional encoding $\text{PE}_i$와 $\text{PE}_{i + \Delta p}$를 dot-product 할 때의 similarity가 오로지 $\Delta p$에 의존할 수 있게 된다는 걸 증명하고 있다.

Learning Rate Scheduler
보통 딥 러닝에서 최적의 gradient descent를 찾아주도록 하는 optimizer 중 자주 사용되는 Adam optimizer가 있는데, 이때 손실함수를 줄이는 방향으로 학습을 수행하 가는 과정에서 learning rate라는 파라미터를 한 값으로 고정하여 사용한다. 여기서 learning rate은 optimizer를 통해 gradient descent를 구하여 파라미터를 업데이트할 때 얼마나 gradient 방향으로 이동할지를 결정짓는 파라미터이다.
그러나 "Attention is All You Need" 논문에서의 Transformer 모델에서는 학습 속도를 좀 더 빠르게 하고 좀 더 global minimum으로 잘 수렴할 수 있도록 모델의 성능을 높이고자 learning rate을 학습 과정에서 적절히 변경하는 scheduler를 사용한다.
이 논문에서 사용한 learning rate scheduler는 임의로 파라미터가 초기화되었을 경우를 고려하여 가파른 gradient descent에서 시작할 수 있다는 가정하에 학습 과정의 초반에서 작은 learning rate를 가지도록 했는데, 이는 이동 보폭이 너무 커지지 않도록 하여 극소에 도달했을 때 너무 쉽게 벗어나지 않도록 하는 것을 방지하기 위함이다. 또한 학습 과정에서 iteration을 늘리면서 learning rate도 비례하여 커지게 하는데, 이는 global minimum이 너무 멀리 있어서 빨리 근접해지지 못하는 현상을 예방하고자 하는 것이다.그런데 특정 iteration 임계점에 도달하면 learning rate을 서서히 줄여가도록 한다. 이는 global minimum에 근접했음에도 불구하고 이동 보폭이 너무 커짐으로 인하여 쉽게 빠져나오는 현상을 막고자 하는 목적을 지니고 있다.
이처럼 learning rate scheduler를 사용할 때 경험적으로 transformer가 좋은 성능을 보임을 제시하고 있다.
"Attention is All You Need"에서 알아두면 좋을 네 가지 기법
1. Residual Connection: gradient vanishing 문제를 해결
2. Layer Normalization: 한 instance의 feature에 관해 그 feature 자체를 정규화
3. Positional Encoding: 입력 sequence의 각 token의 위치 정보를 반영하고자 함
4. Learning Rate Scheduler: learning rate을 한 값으로 고정하지 말고 학습 과정에 따라서 변동을 주자
Transformer의 Decoder
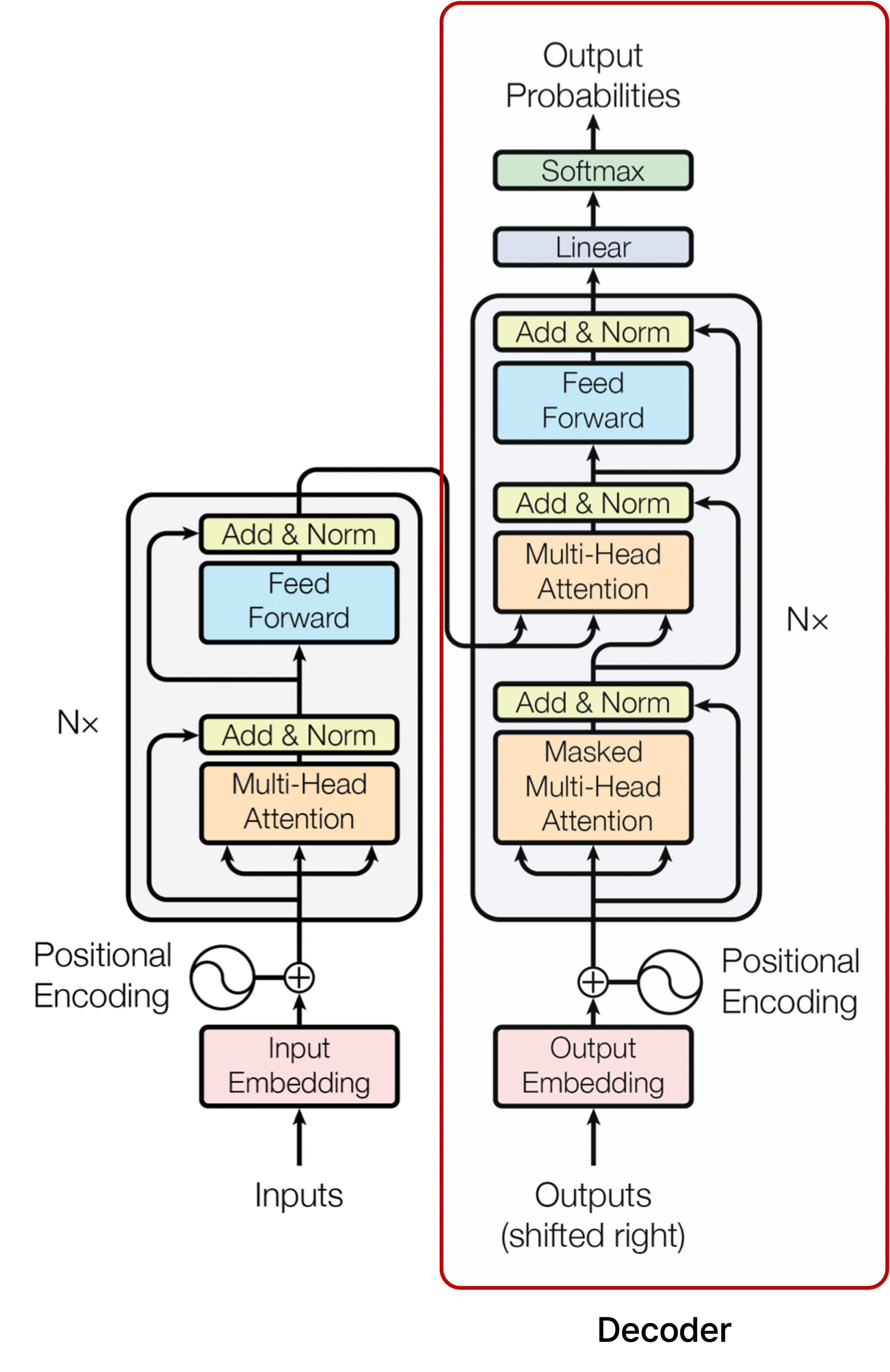
앞에서 살펴 본 내용은 주로 transformer의 encoder에 집중했지만, 입력 sequence를 받아서 출력 sequence를 내는 decoder 부분도 유사한 학습 과정을 거친다.
Decoder에서의 학습 과정

Decoder의 Input
Decoder에서는 입력 sequence에 관하여 ground truth에 해당하는 문장을 오른쪽으로 한 칸 밀어서 실제로 각 단어마다 다음으로 올 단어를 예측하게끔 하는데, 논문에서는 output을 shifted right한 문장을 decoder의 input으로 넣는다고 한다. 하지만 도메인에 따라서 encoder와 decoder의 input sequence 길이가 다를 수 있음에 유의한다.
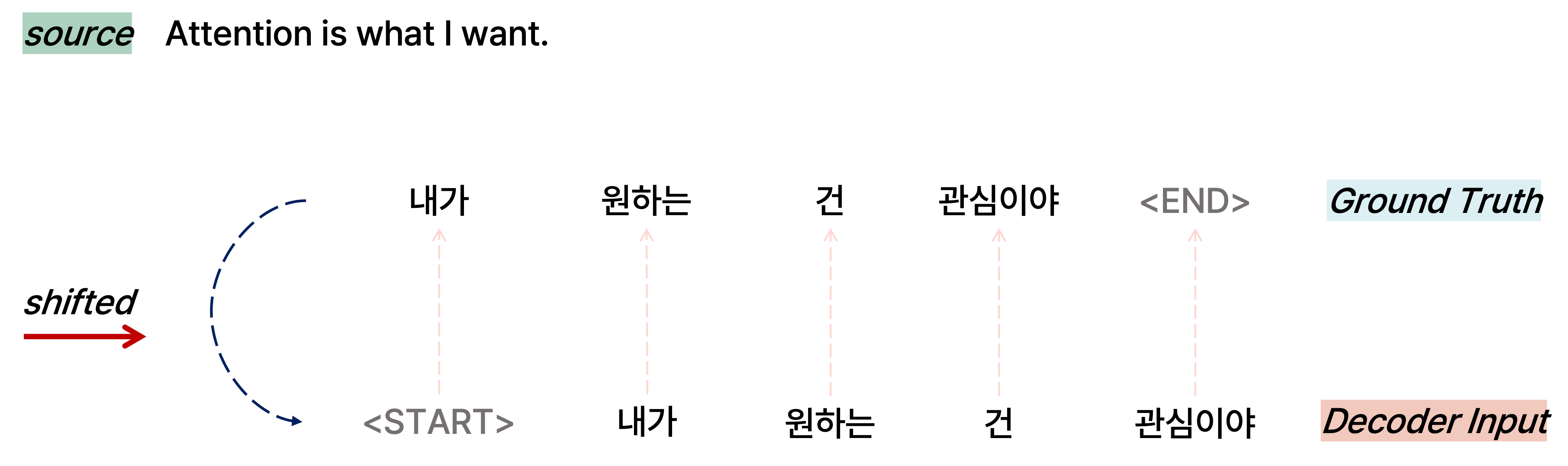
예를 들어, "Attention is what I want"라는 문장을 입력으로 학습하고 ground truth로 "내가 원하는 건 관심이야"라는 문장을 decoder를 통해 예측하도록 학습한다고 가정하자. 그러면 "Attention is what I want" 문장은 transformer의 encoder로 들어가고, "내가 원하는 건 관심이야" ground truth 문장을 오른쪽으로 한 칸 shift한 "내가 원하는 건 관심이야"를 decoder의 입력으로 학습하게 되는 것이다. 이를 통해 각 단어별로 다음 단어를 ground truth로 예측할 수 있도록 모델이 학습을 수행한다.
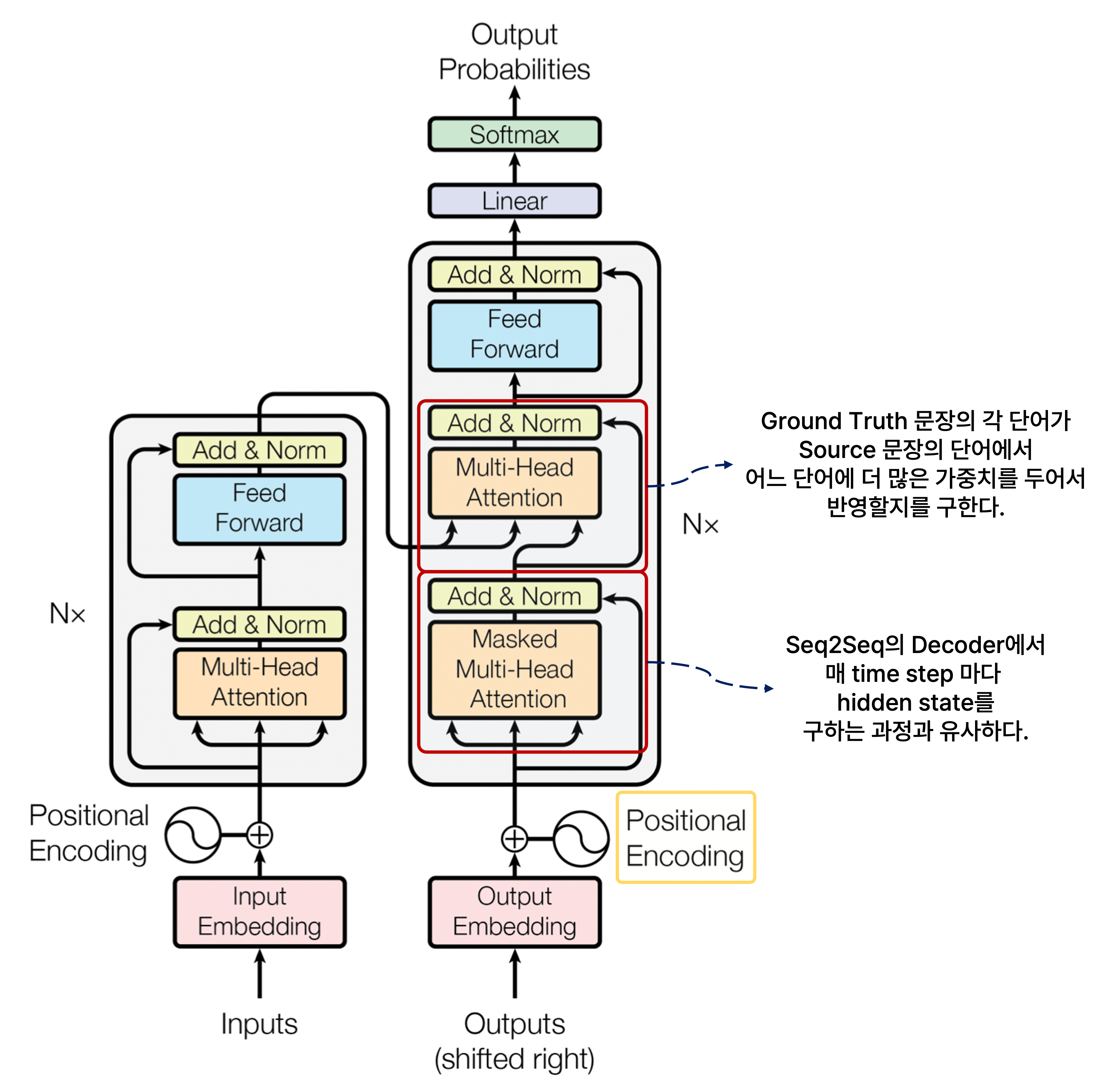
마찬가지로 encoder의 입력 단어별로 적용한 positional encoding을 decoder의 입력에 관해서도 적용한다.
또한 decoder에서도 Masked Multi-Head Attention을 통과시킨 후 residual connection과 layer normalization을 적용하여 ground truth 문장의 각 단어별로 인코딩된 벡터를 갖도록 하는데, 이는 Seq2Seq with Attention의 decoder에서 각 단어에 해당되는 매 time step마다 hidden state를 구하는 과정과 유사하다고 볼 수 있다.
Masked Multi-Head Attention

Decoder에서 ground truth 문장의 각 단어에 관해 query, key, value vector를 만들어서 각 단어별 encoding vector를 만들고자 할 때, 앞에서 등장한 단어가 뒤에서 등장한 단어에 관해 가중치를 부여하여 파라미터 업데이트에 반영하는 경우가 과연 옳은 것인지를 고민해 볼 필요가 있다.
예를 들어, token은 그 이후에 등장하는 단어 정보에 관해 인코딩된 벡터를 생성하게 되면 이는 결과적으로 앞 단어의 인코딩 벡터가 뒤의 단어의 정보도 반영하게 되는 현상이 발생한다.

이러한 문제 발생을 막고자 query와 key vector 간의 내적을 통해 attention score를 구한 후 해당 index 단어의 뒤에 등장하는 단어와의 attention score는 0으로 만들어서 후처리하는 것이 바로 Masked Multi-Head Attention의 핵심이다. 이는 앞에 등장하는 단어를 인코딩할 때 뒤에 등장하는 단어의 정보를 반영하지 못하도록 정보의 접근 권한을 차단하는 역할을 한다고 볼 수 있다.
요약하자면, masking은 self-attention 수행 시 행렬 Q와 K를 곱한 결과인 가중치 행렬에 적용하는데, 이는 self-attention 수행 시 앞 단어를 예측할 때 뒤쪽의 정보가 반영되는 것을 사전에 차단하기 위한 용도이다.
Multi-Head Cross Attention

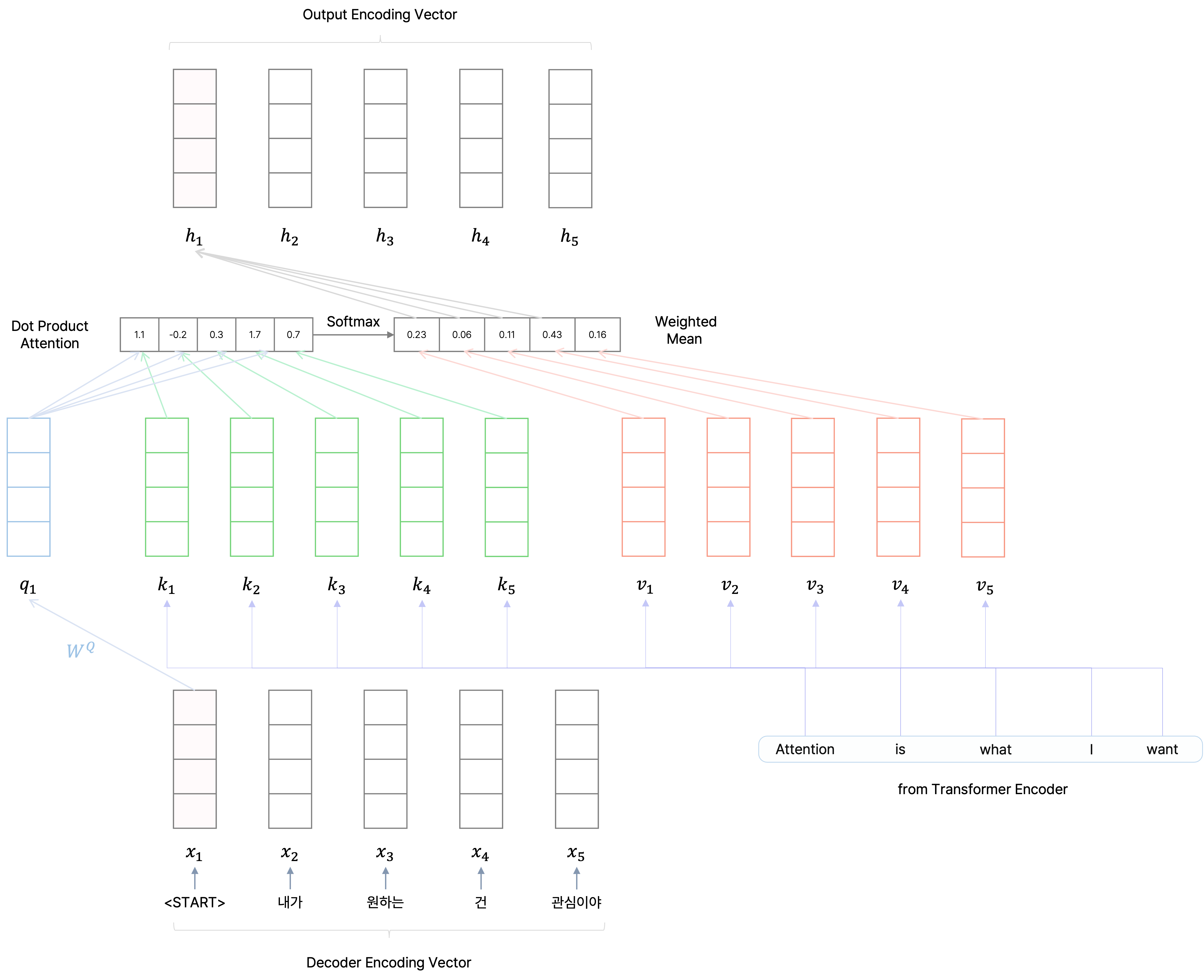
나아가 마찬가지로 Multi-Head Attention과 residual connection, layer normalization을 한 번 더 거치는데, 여기서는 encoder에서 각 단어별로 최종 인코딩된 벡터를 key와 value vector로 사용하고, query vector로는 decoder의 앞단에서 인코딩된 단어별 벡터를 사용한다.
이는 ground truth의 각 단어들이 encoder의 입력으로 주어지는 입력 문장에서 어떠한 단어에 더 주목할지를 구하고, ground truth 문장의 각 단어를 인코딩할 때 encoder의 입력 문장에서 어떠한 단어의 인코딩 벡터를 더 많이 반영할지를 가중 평균 구하는 것으로 해석할 수 있다.
마찬가지로 이를 Seq2Seq with Attention와 대응시켜면, decoder에서 각 단어에 해당되는 매 time step마다 hidden state를 가지고 encoder에서의 모든 hidden state와 attention score를 구한 후 가중 평균을 계산하여 decoder에서 해당 time step에서의 최종 인코딩된 hidden state vector를 구하는 과정으로 볼 수 있다.
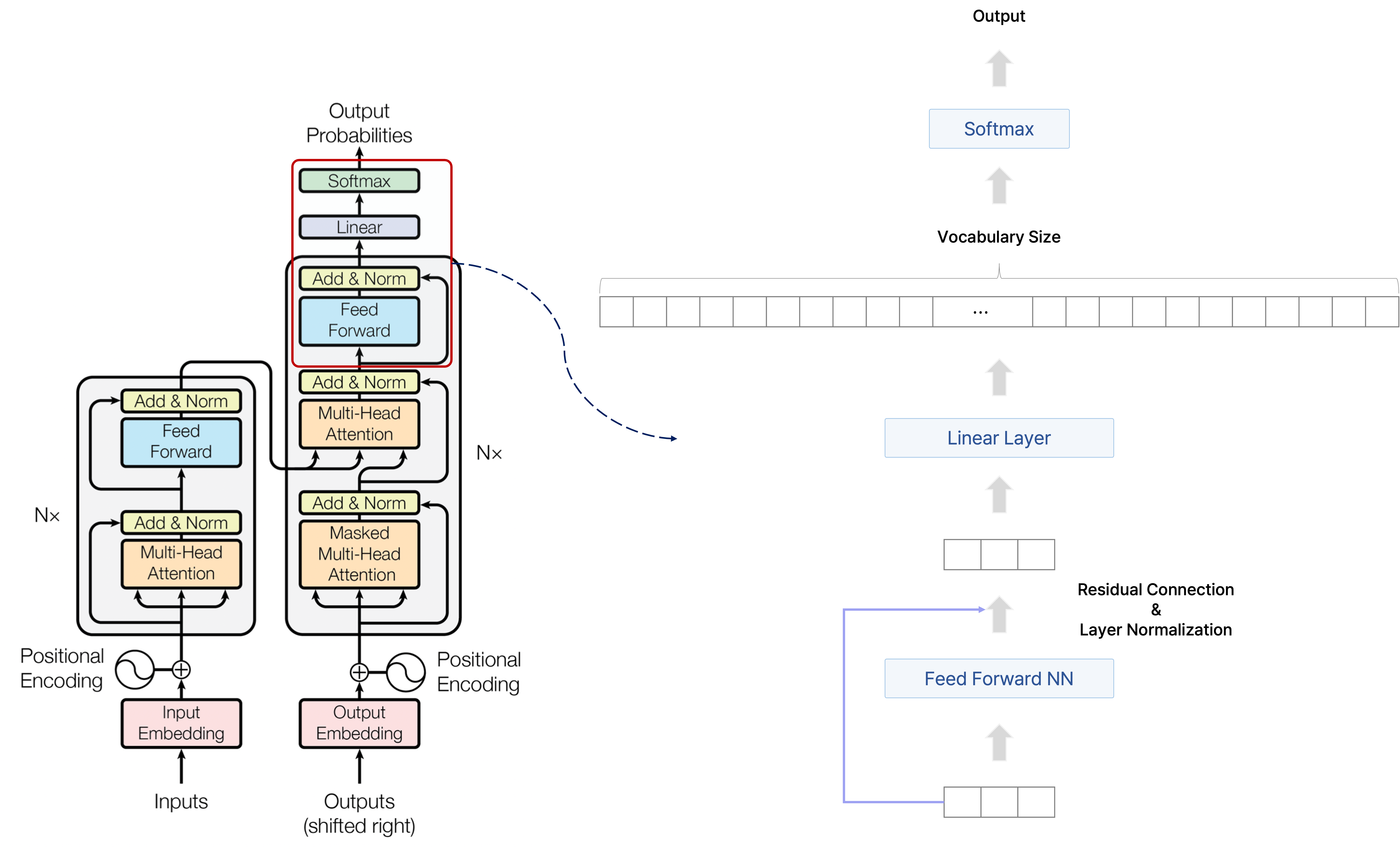
마지막으로 encoder에서와 같이 feed forward neural network를 통과시켜서 residual connection과 layer normalization을 적용하여 ground truth 문장의 각 단어별로 최종 인코딩된 단어 벡터를 얻는다.
더 나아가 decoder에서는 각 단어별로 인코딩된 벡터를 선형 변환 layer를 통과시켜서 target 언어의 vocabulary size만큼의 차원을 갖는 벡터를 만들도록 변환하고, 여기서 softmax를 취해서 해당 index의 단어에서는 다음 단어로 어떠한 단어가 올 가능성이 높은지 그 확률 분포를 구한다.
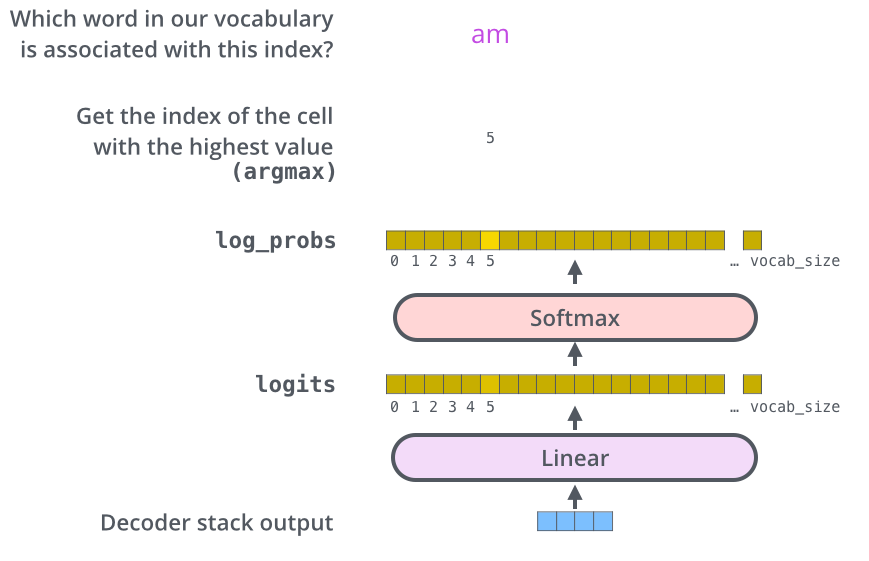
[출처] https://jalammar.github.io/illustrated-transformer, Jay Alammar
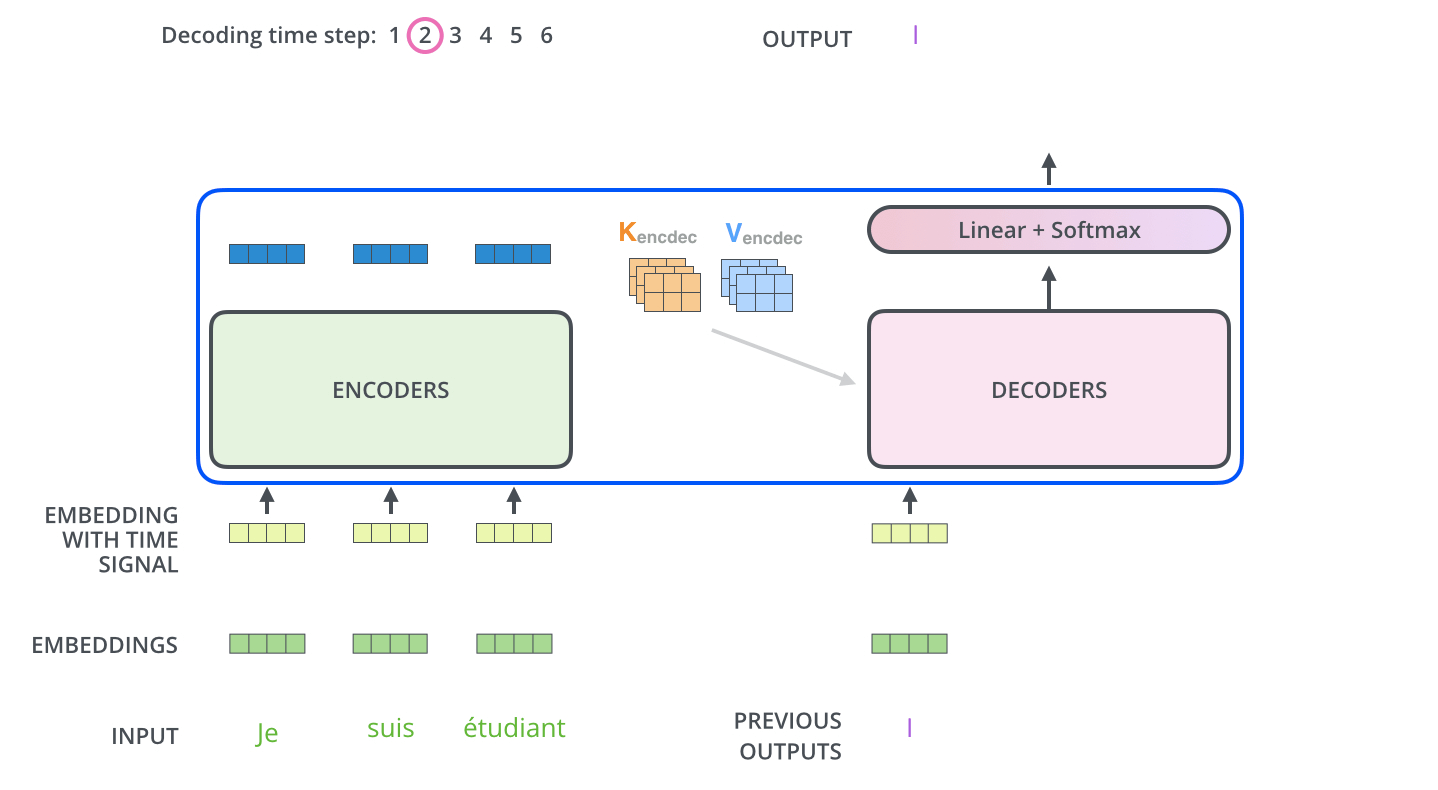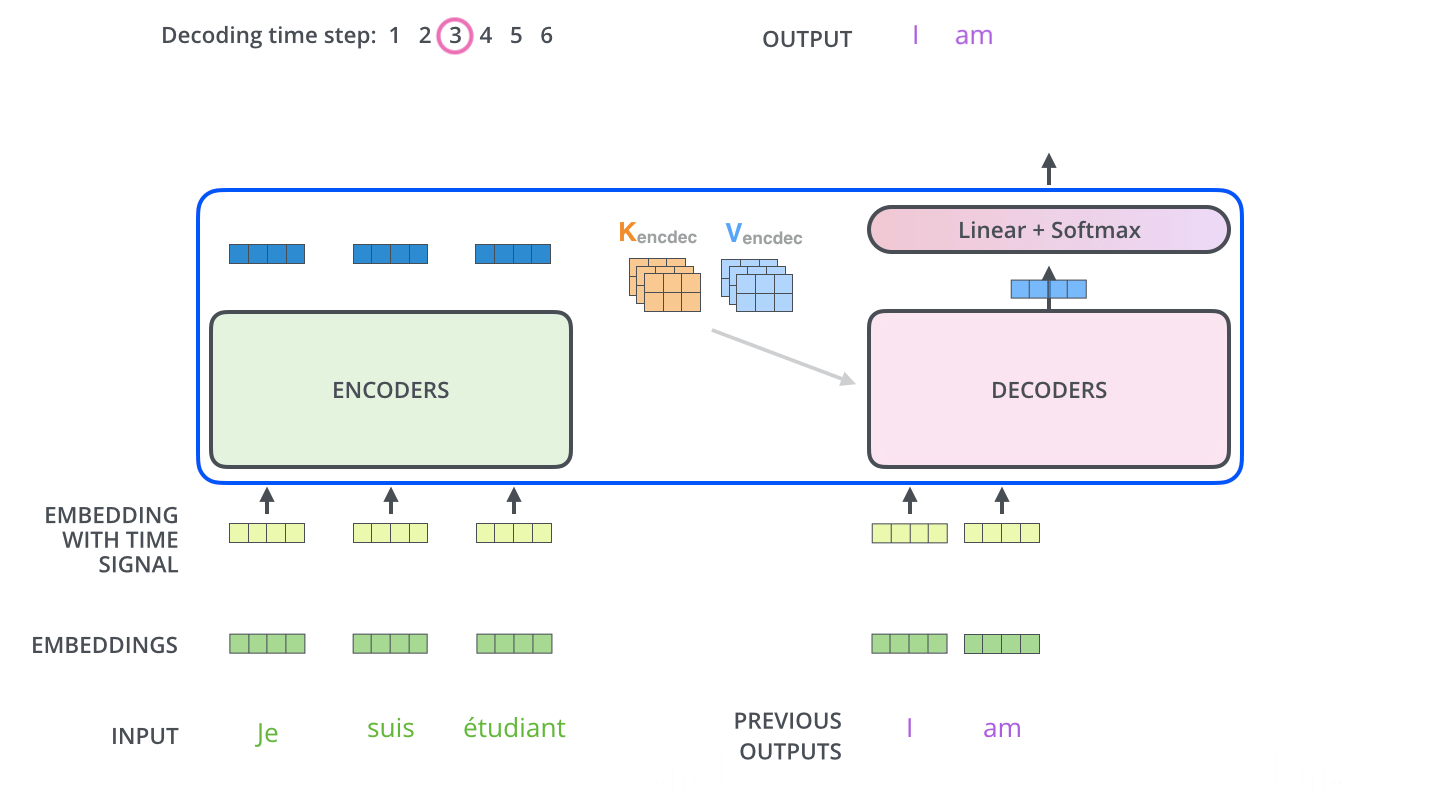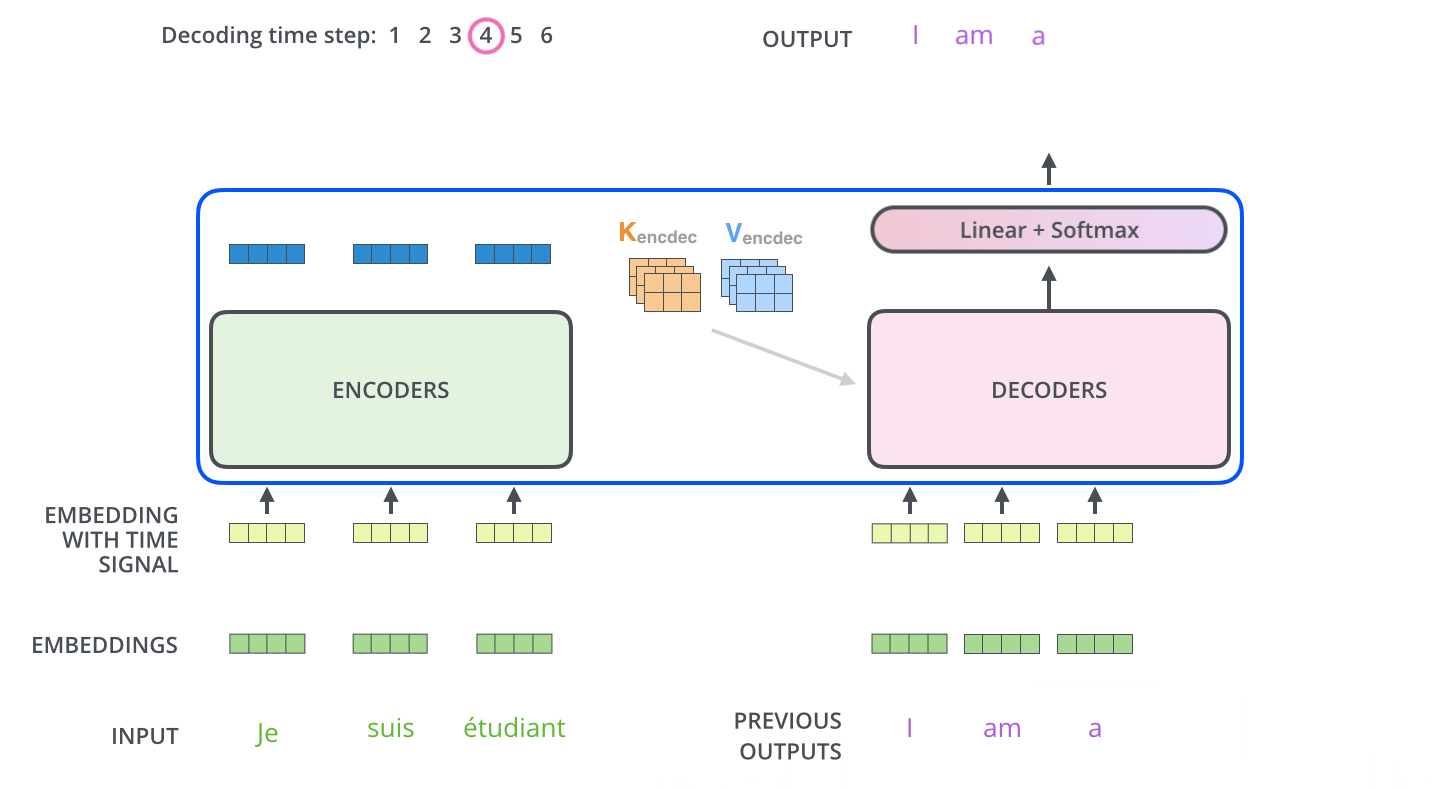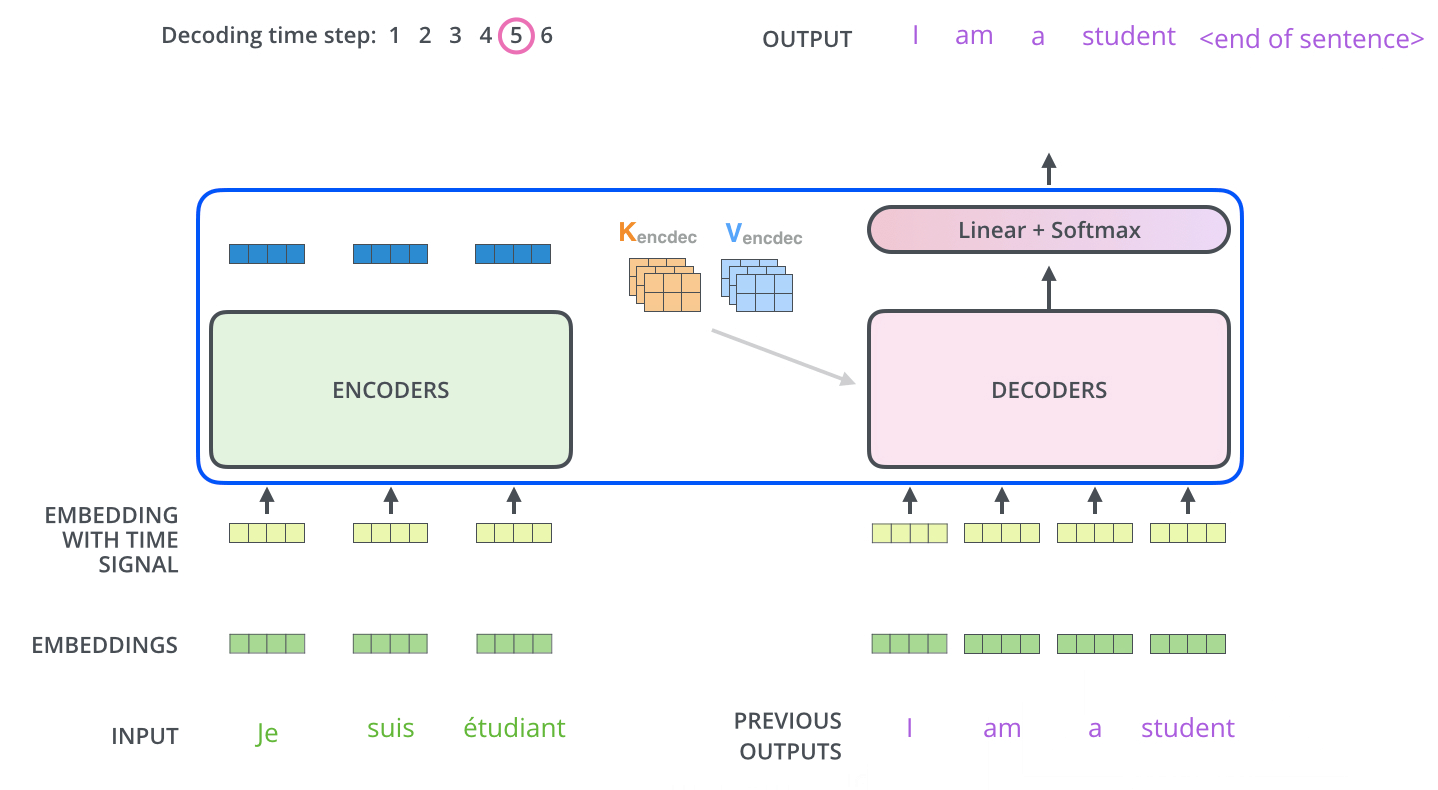
이를 통해 가장 높은 확률 값을 보이는 단어가 해당 Index의 다음 단어로 온다고 예측하는 것이며, 이 예측 단어가 실제 ground truth 문장에서 shift 되기 전 문장의 단어가 나오게끔 오차를 줄이는 방향으로 학습을 진행하는 것이다. 현재까지 설명한 것이 decoding time의 하나의 step을 수행하는 과정이며, 이를 decoder의 input sequence의 길이만큼 time step을 밟으면서 문장 끝까지 수행한다.
Transformer의 전체 구조와 학습 과정

[출처] https://arxiv.org/pdf/1706.03762.pdf, Attention is All You Need
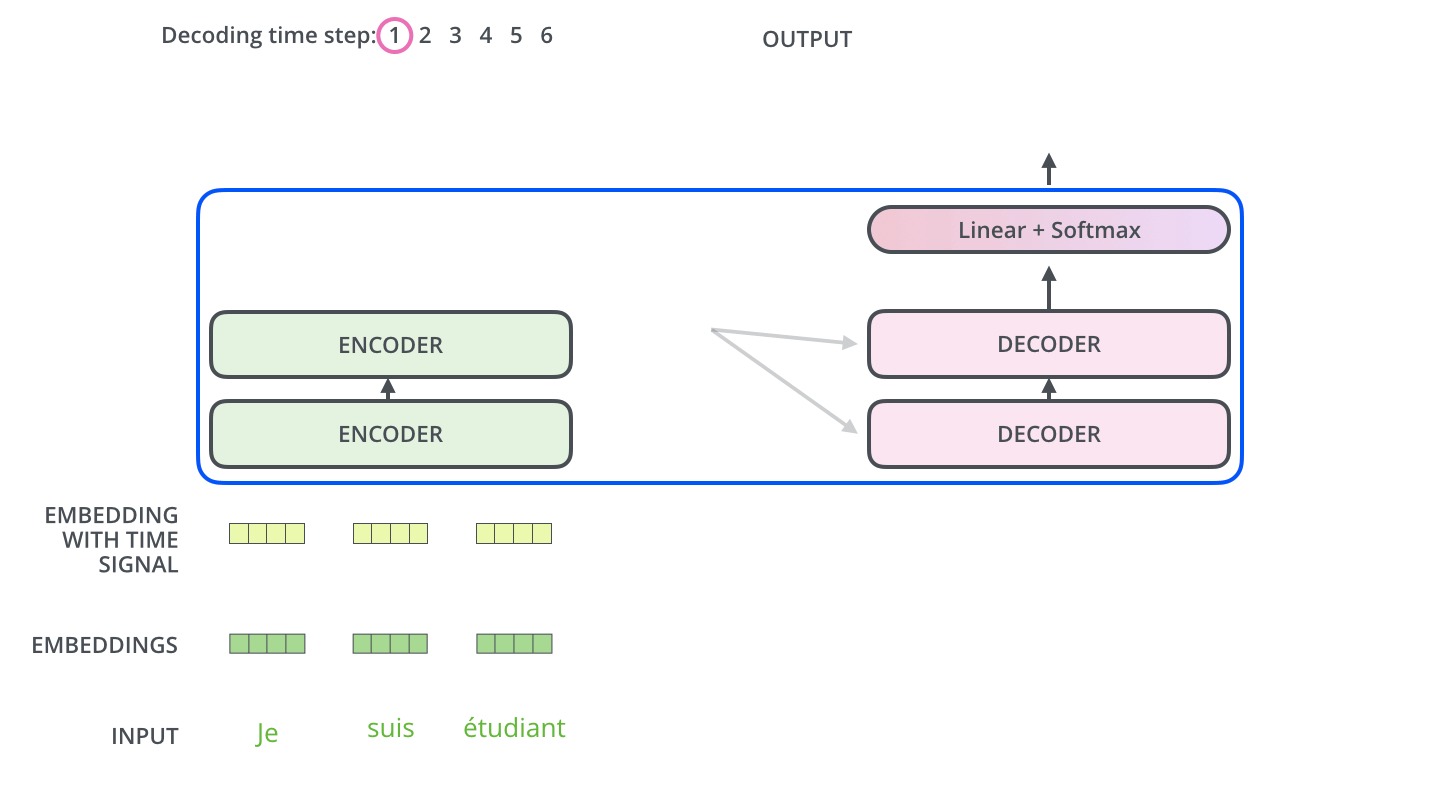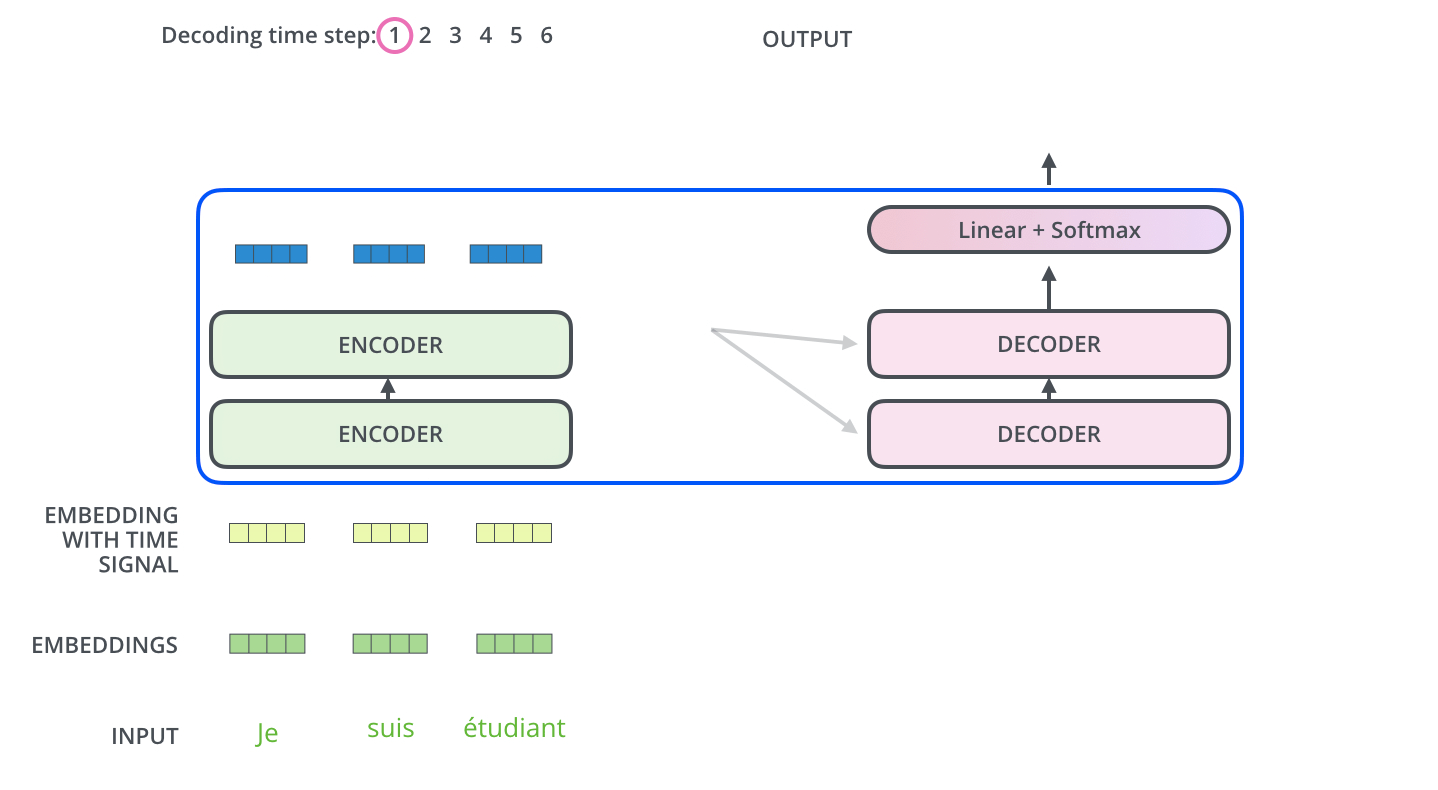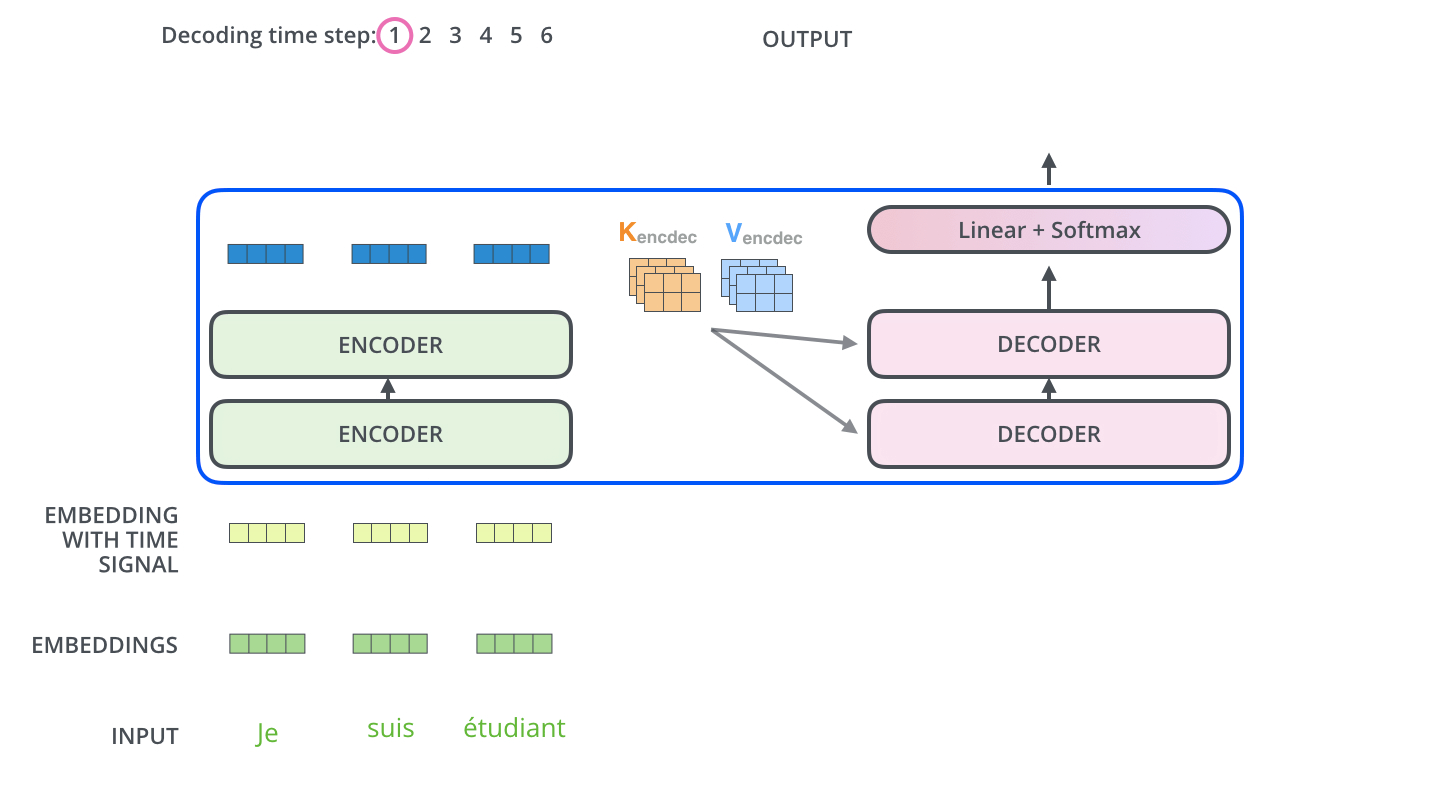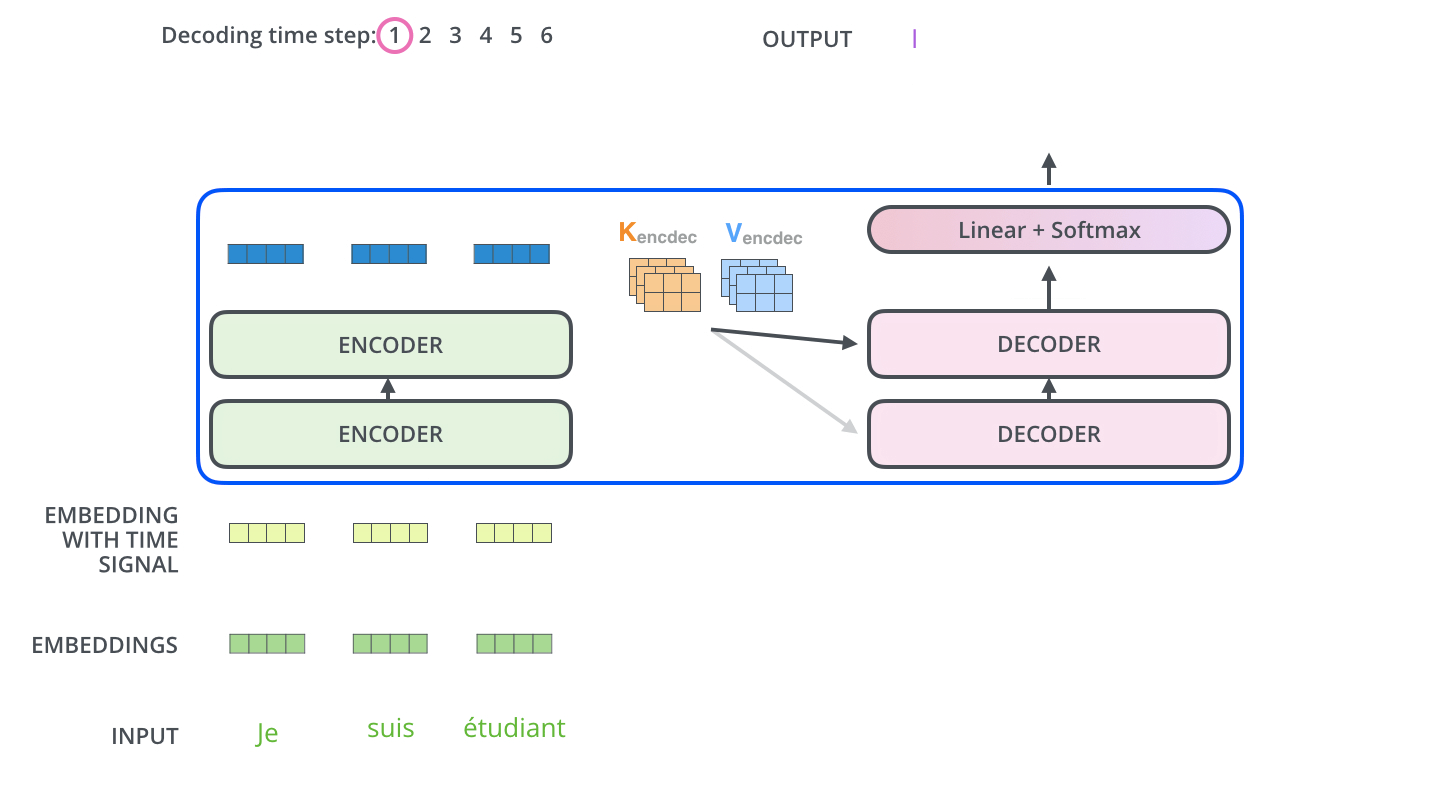
[출처] https://jalammar.github.io, Jay Alammar
- Encoding block을 사용하여 입력에 관해 인코딩된 벡터를 구한다. (Encoder의 전 과정은 한 번만 실행한다.)
- 입력 임베딩 벡터에 Positional Encoding을 적용하여 단어별로 위치에 관한 정보를 지니게 한다.
- Multi-Head Attention 모듈을 통과시킨다.
- Positional Encoding된 입력 벡터에 관해 여러 개의 head마다 query, key, value vector를 만든다.
- 여러 개의 head에서 attention score를 통해 value vector를 가중 평균하여 나온 인코딩된 출력 벡터를 모두 concatenation한다.
- 이를 Multi-Head Attention 모듈의 output layer를 통과시켜서 입력 벡터의 차원과 같은 크기의 차원을 지니는 최종 출력 인코딩 벡터를 구한다.
- Residual connection을 통해 입력 벡터와 Multi-Head Attention의 최종 출력 인코딩 벡터를 더하고, layer normalization을 적용한다.
- Feed forward neural netwrok을 통과시켜서 residual connection과 Layer normalization을 적용한다.
- 이러한 encoding block이 $N$개라면 위의 과정을 $N$번 반복하여 $N$개의 encoding block을 거친다.
- Encoder의 output으로는 input의 각 단어에 관한 context vector를 얻는 것이며, 이들은 decoder의 multi-head cross attention에서 key와 value vector로 사용된다.
- Decoding block을 사용하여 ground truth 문장에서 다음 단어로 어떠한 단어가 와야 하는지를 학습한다. 다음 단어를 예측할 때마다 그 예측 단어를 decoder의 입력 sequence에 넣음으로써 문장 끝까지 예측을 반복 수행한다.
(Encoder는 한번에 수행하지만 decoder에서는 decoding time step별로 수행하여 문장 끝까지 수행한다는 점을 유의한다.)- GT(Ground Truth) 문장을 오른쪽으로 한 칸 shift한 후(도메인에 따라 달리 구현될 수 있으며, 어디까지나 이 논문의 NLP task 구현 예시) positional encoding을 적용하여 GT 문장의 각 단어에 관한 임베딩 벡터를 구한다.
- Masked Multi-Head Attention을 통해 GT 문장의 각 단어의 임베딩 벡터에 관해 인코딩된 벡터를 구한다.
- Positional Encoding된 GT 문장의 각 단어별 임베딩 벡터에 관해 여러 개의 head 마다 query, key, value vector를 만든다.
- 앞에 등장한 단어의 인코딩된 벡터가 뒤에 등장하는 단어의 정보를 반영하지 못하도록 query와 key vector의 연산 결과에서 뒤에 등장하는 단어 쌍으로 나온 attention score는 0으로 만드는 과정이 포함된다.
- Residual connection을 통해 입력 벡터와 Multi-Head Attention의 최종 출력 인코딩 벡터를 더하고, layer normalization을 적용한다.
- Multi-Head Attention을 한 번 더 거친다.
- 앞서 나온 GT 문장의 각 단어별 인코딩 벡터를 가지고 query vector를 만든다.
- Encoding block에서 나온 각 단어별 최종 인코딩 벡터를 가지고 key, value vector를 만든다.
- GT 문장의 각 단어가 Encoding block 입력 문장에서 어떠한 단어를 더 많이 반영할지 구하여 인코딩 벡터를 구한다.
- 마찬가지로 Residual connection을 통해 입력 벡터와 Multi-Head Attention의 최종 출력 인코딩 벡터를 더하고, layer normalization을 적용한다.
- Feed forward neural netwrok을 통과시켜서 residual connection과 Layer normalization을 적용한다.
- 이러한 decoding block이 $N$개라면 위의 과정을 $N$번 반복하여 $N$개의 decoding block을 거친다.
- GT 문장의 각 단어별 최종 인코딩 벡터를 가지고 선형 변환 레이어에 통과시켜서 vocabulary size만큼의 차원을 갖는 벡터로 만든다.
- 각 단어별로 선형변환한 결과 벡터에 softmax를 적용하여 어떠한 단어가 다음 단어로 올 확률이 높은지 그 분포를 구한다.
- 최종적으로 다음에 올 것으로 예측한 단어가 실제 다음으로 오는 단어와 같도록 오차(cross entropy)를 줄이는 방향으로 학습한다.
출처
1. 네이버 커넥트재단 부스트캠프 AI Tech NLP Track 주재걸 교수님 기초 강의
2. Jay Alammar, https://jalammar.github.io/illustrated-transformer
업데이트
1. Layer normalizaion에서 잘못 서술된 내용(batch normalization, layer normalization)이 수정되었습니다. (2023. 02. 06)
2. Positional encoding에서 sinusoidal 함수를 사용하는 이유가 추가되었습니다. (2023. 04. 06)
3. Transformer를 정리한 그림 이미지를 첨부했습니다. (2023. 04. 11)
'AI > AI 기본' 카테고리의 다른 글
| VAE 계열 모델의 ELBO(Evidence Lower Bound) 분석 (0) | 2023.05.23 |
|---|---|
| Hidden Markov Model과 Filtering, Forwarding 그리고 Viterbi Algorithm (0) | 2023.04.13 |
| [인공지능 기초] Adversarial Search - Minimax Search와 Alpha-beta Pruning (0) | 2022.10.09 |
| Transformer를 사용하는 것이 항상 좋을까? (0) | 2022.08.31 |
| Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교 (0) | 2022.07.23 |
소중한 공감 감사합니다.