[인공지능 기초] Adversarial Search - Minimax Search와 Alpha-beta Pruning
- -
Adversarial Search
Adversarial Search란?
Adversarial search는 '적대적인'이라는 'adversarial'의 의미에서 유추할 수 있는 것처럼 둘 이상의 대상(multi-agent)이 서로 다른 목표를 달성하기 위해 적대적인 관계에서 경쟁하는 것이다. 다른 대상의 행동이 자신의 성공에 영향을 끼치므로 자신의 목표를 달성하기 위해 최선의 행동을 선택할 때 다른 대상이 선택할 가능성이 있는 행동을 모두 고려해야 한다. 우리가 일상에서 자주 하는 게임(game)이 바로 대표적인 adversarial search이며, 자신이 이기기 위해 다른 플레이어의 행동을 고려하여 가장 좋은 수를 선택하려고 한다. 이러한 맥락에서 adversarial search를 game search라고도 한다.
Game
Game의 종류
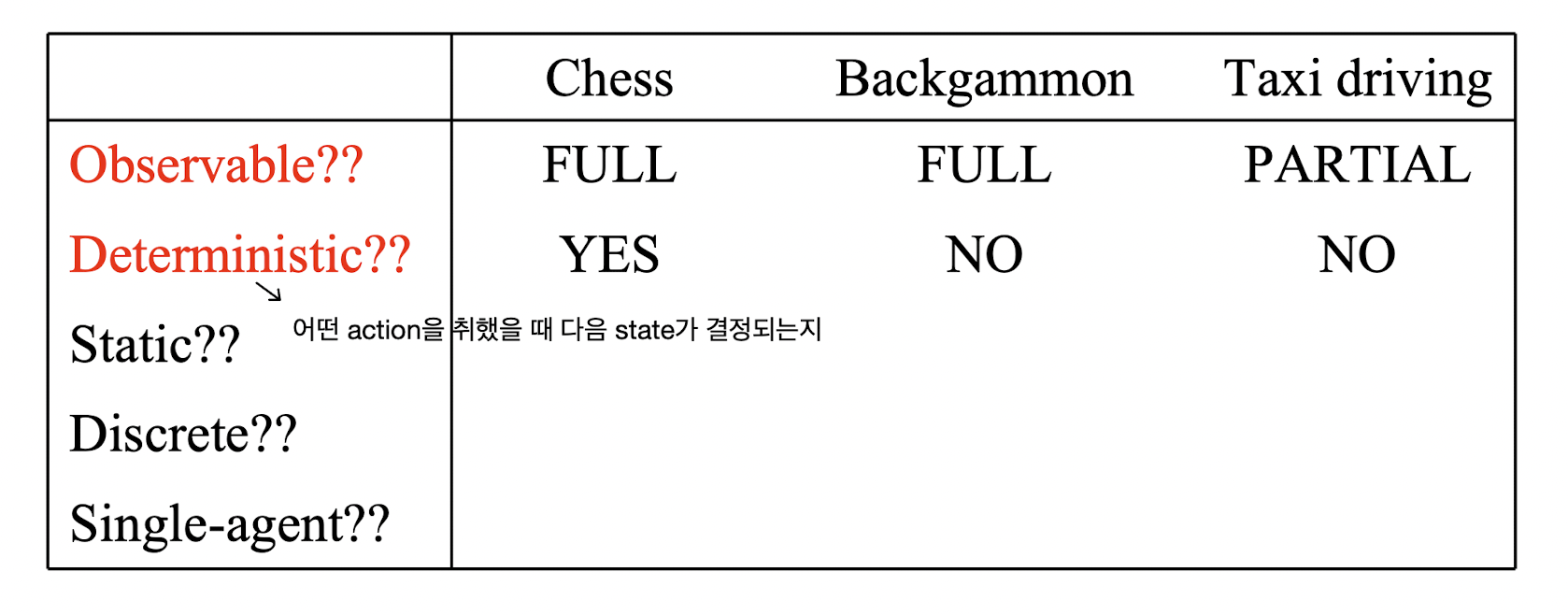
Agent가 수행하는 task인 게임의 환경(environment)을 범주화했을 때 결정적(deterministic)인지 확률적(stochastic)인지를 분류할 수 있는데, 여기서 결정적(deterministic)이란 건 현재 state에서 가능한 임의의 한 action을 취했을 때 다음 state가 결정된다는 말이다. Chess와 checker 같이 하나의 판을 공유한 상황에서 서로 다른 플레이어가 수를 번갈아 두는 게임에서는 임의의 상태에서 어떤 한 플레이어가 어떤 행동을 할지 선택하면 다음 상태가 결정된다. 그러나 backgammon과 같이 어떤 플레이어가 임의의 한 행동을 한다고 해서 다음 상태가 확실히 결정되지 않고 확률에 의해 결정된다면 이는 deterministic하지 않은 게임이라고 볼 수 있다. (사실 개인적으로 backgammon을 해본 적이 없어서 어떤 게임인지 잘 모르긴 하지만... 그렇다고 한다. 😅)
Chess에서는 하나의 판이 자신과 상대방에게 모두 공개되므로 자신도 상대방의 정보를 완전히 알 수 있다. 그러나 poker와 같이 자신과 상대방의 상태가 모두 공개되지 않고 자신의 상태만 알고 있는 게임도 있는데, 이를 imperfect information이라고 한다.
이번 글에서는 현재 상태에서 모든 정보를 알 수 있고 결정적인 환경에서 이루어지는 게임(deterministic game with perfect information)을 다룰 것이다.
Zero-sum Game
Zero-sum game은 어떤 한 플레이어에게 좋은 건 반대로 다른 플레이어에게는 나쁜 게임을 의미하며, 이 게임에서는 두 플레이어가 모두 좋은 경우는 없다. 즉, 자신이 점수를 얻으면 상대방은 결국 점수를 잃는 것이고, 두 사람의 결과를 더해보면 0이 되는 것이다.
우리가 살펴볼 게임도 바로 누군가는 승리할 때 상대방은 패배하고, 그렇지 않으면 동률인 결과를 내는 것이다. 다시 말해, 두 플레이어가 모두 승리하는 게임이 아니다.
Minimax Search
Minimax Search란?
Minimax search를 살펴보기 전에 우리가 앞에서 전제한 게임을 하는 상황을 상상해보자. 게임의 플레이어는 나와 상대방인 2명이고, 내가 먼저 시작해서 상대방과 번갈아 가면서 게임을 플레이한다고 가정한다. 또한 게임이 종료되었을 때 점수를 상대방보다 많이 얻는 사람이 승리한다고 하자. 그러면 나는 최선을 다해 게임에 임할 것이므로 무작정 아무런 수를 두지 않을 거다. 내가 어떠한 수를 두었을 때 상대방이 어떻게 행동할지를 고려하고, 그중에서 당연히 내게 가장 좋은 결과를 가져오는 수를 선택할 것이다.
우리가 전제한 게임의 승리 조건은 상대방보다 더 높은 점수를 획득하는 것이므로, 수를 택할 때 우리는 자신에게 가장 높은 점수를 가져오는 행동을 할 거라고 자연스럽게 예상할 수 있다. 상대방도 승리를 위해 상대방 입장에서 가장 높은 점수를 가져오는 수를 택할 텐데, 이를 반대로 생각하면 결국 상대방은 나를 지게 만드는 수를 고르는 것이다. 즉, 내가 어떠한 수를 고를 때 상대방이 어떻게 행동할까를 생각하면, 상대방은 나를 지게끔 만들기 위해 가장 낮은 점수를 가져오는 수를 택한다고 예상할 수 있다.
Minimax Search의 구성 요소
이러한 아이디어를 가지고 게임을 좀 더 일반화하여 필요한 요소를 정의해보자.
- Initial state: 초기 상태
Player(state): 상태state에서 어떤 플레이어가 행동을 취할 수 있는지를 반환하는 함수Actions(state): 상태state에서 플레이어가 택할 수 있는 행동을 반환하는 함수- Terminal state: 게임이 종료되는 최후의 상태
Terminal-test(state): 상태state가 terminal state인지를 반환하는 함수Utility-function(state, player): Terminal state인state에서 특정 플레이어player가 지닐 수 있는 값을 반환하는 함수
위의 정의한 내용이 추상적일 수 있지만 너무 어렵게 생각할 필요가 없다. 앞서 가정한 게임에 응용하여 정리해보자.
- 우리는 게임을 초기 상태부터 시작할 텐데, 보통 초기 상태는 나와 상대방 모두 아무런 수를 두지 않은 상태일 것이다.
Player(state)는 각각의 상태마다 어떠한 플레이어가 행동을 취할 수 있는지를 반환한다고 정의했는데, 앞에서 가정한 바에 따르면 나와 상대방이 번갈아 가면서 수를 둔다고 했으므로 '번갈아 가면서 수를 둔다'의 구현이 바로 함수의 내용이다.- 각각의 상태마다 나 또는 상대방이 놓을 수 있는 수가 다를 것이다. 예를 들어, 게임에서 상대방이 놓은 marker의 인접한 킨에는 나의 marker를 놓을 수 없다고 가정할 때,
Actions(state)은 상대방의 marker에 인접한 칸이 아닌 다른 칸에 나의 marker를 놓는 행동들을 반환한다. - 게임이 종료되는 상태는 나 또는 상대방이 더 이상 아무런 수를 둘 수 없는 상태이다.
- 현재 도달한 상태가 나 또는 상대방이 더 이상 아무런 수를 둘 수 없는 상태인지를 판단하는 함수가
Terminal-test(state)이다. Utility-function(state, player)함수는 게임이 종료되는 상태에서 내가 얻을 수 있는 점수가 몇 점인지를 반환한다. 만약에 최후 상태에서 얻을 수 있는 점수가 승패의 결정 조건이 아니라 단순히 승패 여부가 결정된다면 내가 이길 때를+1, 나와 상대방이 비길 때는0, 내가 지면-1을 반환한다고 정의할 수 있을 것이다.
Minimax Search의 핵심 가정
위에서 정의한 내용에 입각하여 앞서 살펴 본 아이디어를 정리하면 다음과 같다.
나는 승리를 위해 최종적으로
Utility-function값이 최대가 될 수 있는 행동을 택하고, 상대방은 나를 패배하게 만들기 위해 최종적으로Utility-function값이 최소가 될 수 있는 행동을 택할 것이다.
나는 Utility-function 값이 최대가 될 수 있는 행동을 하므로 나를 MAX 플레이어라고 하고, 반대로 상대방은 Utility-function 값이 최소가 될 수 있는 행동을 하므로 상대방을 MIN 플레이어라는 이름을 붙일 수 있다. 'Minimax search'라는 이름은 바로 MAX와 MIN 플레이어가 각자의 목표를 위해 최선을 다해 싸우는 환경에서 특정 플레이어에게 가장 좋은 전략을 찾는다는 의미를 내포하고 있다고 볼 수 있다.
Minimax search에서 상대방은 나를 지게끔 만들기 위해 최선의 행동을 고른다는 가정을 바탕으로 내가 택할 수 있는 최선의 선택을 고른다. 그런데 만약에 상대방이 최선의 행동을 고르지 않고 실수를 한다면 어떻게 되는지 궁금할 수 있다. 그렇다고 하더라도 나는 결국 최선의 행동을 택하는 것이므로 위와 같은 가정으로 행동을 택하는 것이 확률적으로 더 좋은 선택임은 부정할 수 없다. 오히려 상대방의 실수는 내게 더 고마운 것이다. 😆
개인적으로 아래의 문장은 minimax search의 내용을 잘 함축하고 있다고 본다.
"Minimax search maximizes the worst-case outcome for max."
상대방인 MIN 플레이어가 나를 지게 만들기 위해 최선의 선택을 하는 worst-case에서 MAX 플레이어의 결과를 최대화하는 행동을 택한다는 의미를 담고 있다.
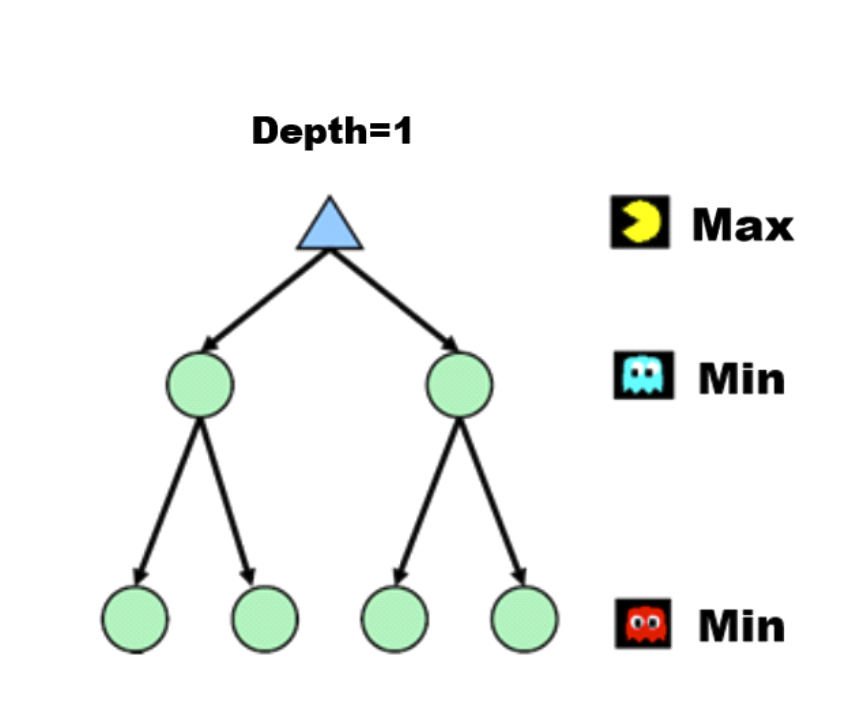
Minimax Search의 Tree
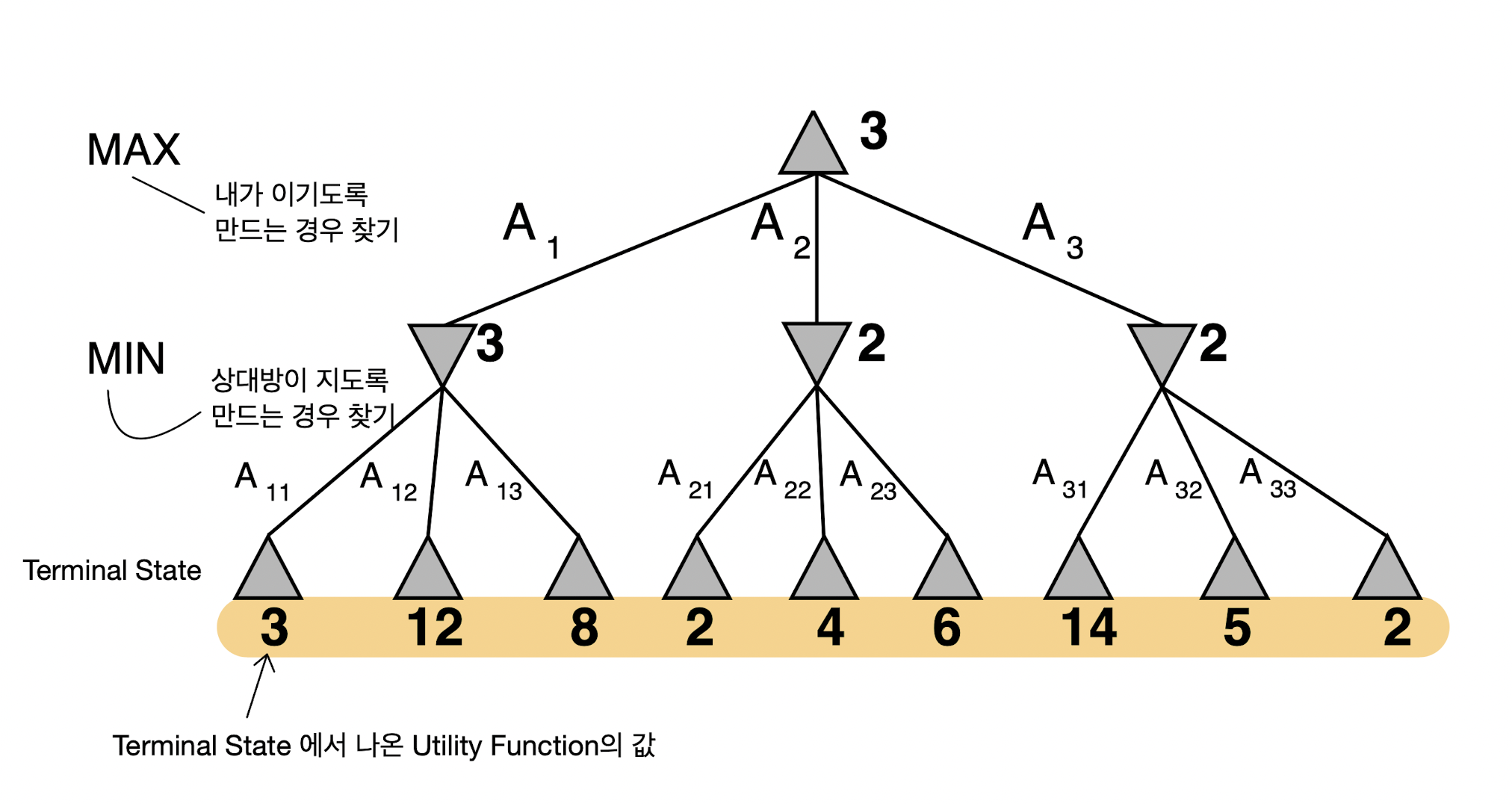
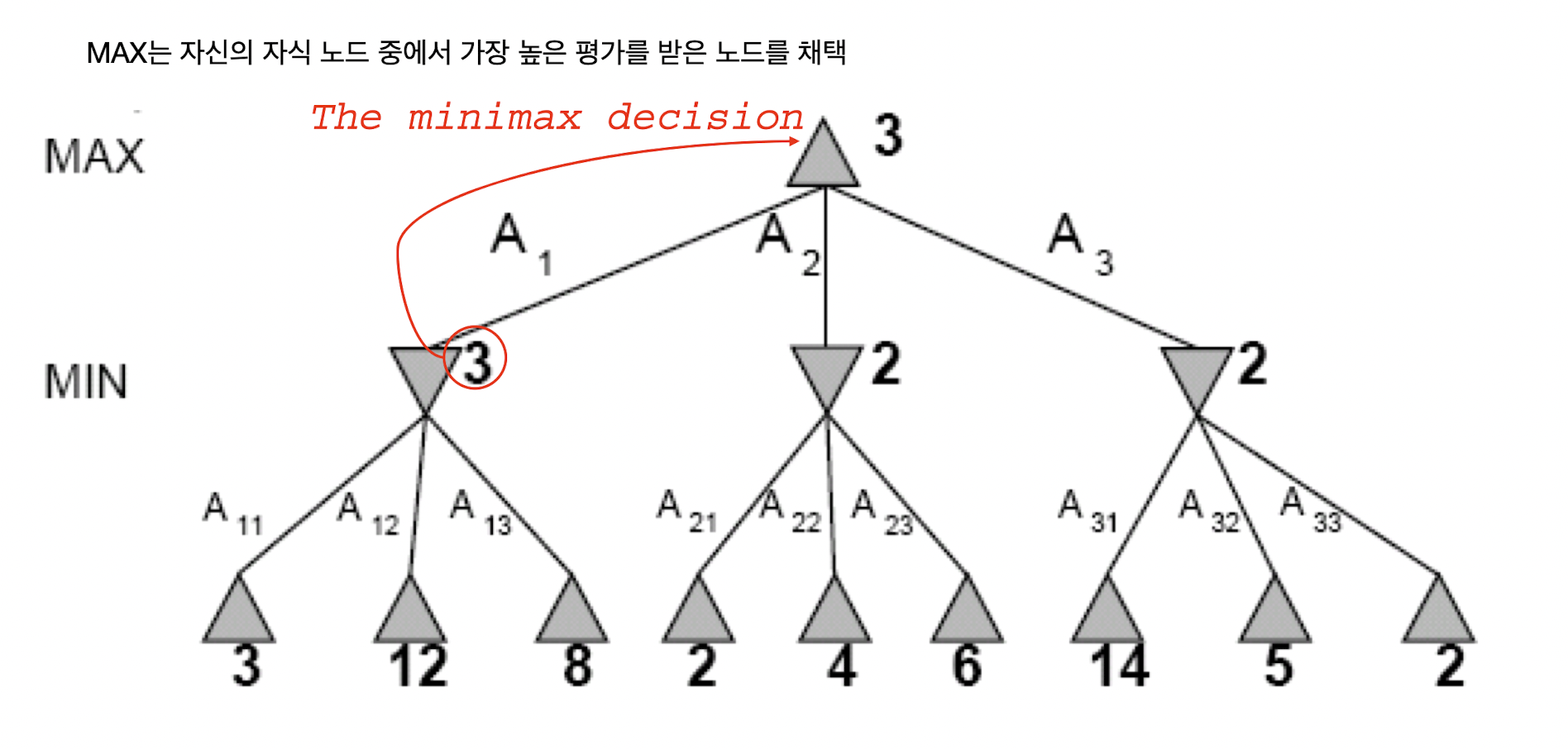
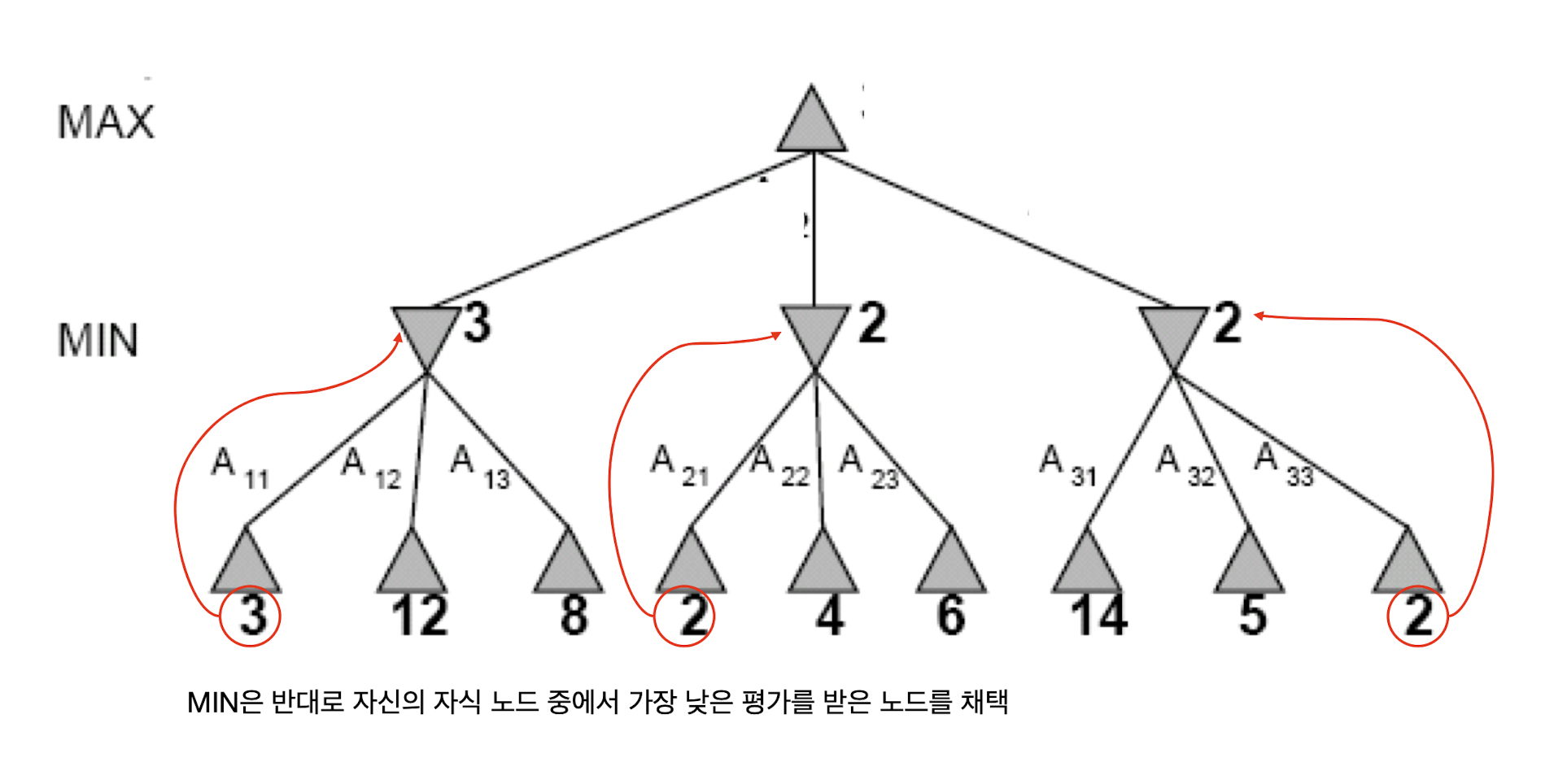
각각의 상태를 노드로 정의하면 초기 상태에서 가능한 행동을 택하면서 뻗어나가는 상태를 그래프로 표현하면 트리 형태를 구성하게 되는데, 이를 'game tree'를 정의한다고 말한다. MAX 플레이어는 MIN 플레이어가 고른 결과를 자식으로 지니게 되고, 그중에서 가장 높은 점수를 지니는 노드의 점수가 자신의 점수로 택한다. 반대로 MIN 플레이어는 MAX 플레이어가 고른 결과를 자식으로 지니게 되고, 그중에서 가장 낮은 점수를 지니는 노드의 점수가 자신의 점수로 택한다. 여기서 노드의 점수를 'minimax value'라고도 하며, 이를 수식으로 정리하면 다음과 같이 쓸 수 있다.
Minimax Search의 알고리즘
Minimax search 알고리즘을 pseudo code로 살펴보면 다음과 같다.

function MINIMAX-SEARCH(game, state) returns an action
player ← game.TO-MOVE(state)
value, move ← MAX-VALUE(game, state)
return move
function MAX-VALUE(game, state) returns a (utility, move) pair
if game.IS-TERMINAL(state) then return game.UTILITY(state, player ), null
v ← -∞
for each a in game.ACTIONS(state) do
v2 , a2 ← MIN-VALUE(game, game.RESULT(state, a))
if v2 > v then
v, move ← v2 , a
return v, move
function MIN-VALUE(game, state) returns a (utility, move) pair
if game.IS-TERMINAL(state) then return game.UTILITY(state, player ), null
v ← ∞
for each a in game.ACTIONS(state) do
v2 , a2 ← MAX-VALUE(game, game.RESULT(state, a))
if v2 < v then
v, move ← v2 , a
return v, move
MAX-VALUE와 MIN-VALUE에서 각각 MAX와 MIN 플레이어가 최선의 행동을 택하는데, MAX 플레이어는 가장 높은 minimax value를 찾고 MIN 플레이어는 가장 낮은 minimax value를 찾을 것이다.
코드를 살펴보면 마치 DFS(Depth-First Search) 같다는 느낌을 지울 수가 없는데, 게임이 종료되는 leaf node가 나올 때까지 한 경로에서 갈 수 있는 한 깊이 탐색해 가는 방법임을 고려해보면 이에 수긍이 간다. Leaf node까지 도달하는 최대 깊이를 $m$, 한 상태에서 뻗어나갈 수 있는 최대 가지 수를 $b$라고 하면 시간복잡도 DFS와 같은 $O(b^m)$이고, 공간복잡도도 DFS와 같은 $O(bm)$이다. 공간복잡도가 잘 이해가 안 간다면 DFS의 stack을 생각해보자. Leaf node까지 도달할 때까지 지나온 경로에 있는 모든 노드의 자식들이 stack에 들어가 있으므로 시작점부터 도착한 leaf node까지의 경로 위에 있는 $m$ 개의 노드에 관해 그 $m$개의 각각의 노드가 지닐 수 있는 최대 $b$ 개의 자식이 stack에 있어야 하는 것이다.
단, 유한한 시간 내에 탐색이 끝나려면 트리가 무한정으로 뻗어나가지 말아야 하며, leaf node까지 도달하는 깊이가 깊어질수록 시간 복잡도는 자연스럽게 커질 수 밖에 없다. 노드가 지닐 수 있는 자식의 수가 적다고 해도 게임이 종료될 때까지 트리를 타고 들어가야 하는 깊이가 너무 크면 기하급수적으로 시간복잡도가 커질 것이다.
예시로 아래는 픽맨 게임 프로젝트를 진행하면서 픽맨이 최선의 행동을 택하기 위해 minimax search를 하는 코드를 작성한 것이다.
def is_terminal(gameState, currentDepth):
return gameState.isWin() or gameState.isLose()
def minimax_search(gameState, depth, agent):
# Pacman is an agent which number is 0
if is_terminal(gameState, depth):
return {'utility': self.utilityFunction(gameState), 'move': None}
agent = agent % gameState.getNumAgents() # Player(state) function
if agent == 0:
return max_value(gameState, depth + 1, agent)
else:
return min_value(gameState, depth, agent)
# Pacman
def max_value(gameState, depth, agent):
highest_value = float("-inf")
possible_moves = gameState.getLegalActions(agent)
best_move = None
for move in possible_moves:
successor = gameState.generateSuccessor(agent, move)
new_value = minimax_search(successor, depth, agent + 1)['utility']
if new_value > highest_value:
highest_value = new_value
best_move = move
return {'utility': highest_value, 'move': best_move}
# Ghost
def min_value(gameState, depth, agent):
lowest_value = float("inf")
possible_moves = gameState.getLegalActions(agent)
best_move = None
for move in possible_moves:
successor = gameState.generateSuccessor(agent, move)
new_value = minimax_search(successor, depth, agent + 1)['utility']
if new_value < lowest_value:
lowest_value = new_value
best_move = move
return {'utility': lowest_value, 'move': best_move}
minimax_search(gameState, 0, 0)['move']
팩맨 게임에서는 두 유령이 있고 팩맨은 게임의 맵에서 많은 원을 먹기 위해 노력하고, 유령은 팩맨이 많은 원을 먹지 못하도록 팩맨을 잡으러 갈 것이다. 플레이어의 수는 팩맨과 두 유령을 더하여 셋이므로 Player(state) 함수가 앞서 본 예제처럼 번갈아가지 않고 플레이어의 수를 주기로 돌면서 팩맨의 순서에 왔을 떄는 MAX 플레이어의 행동을, 유령의 순서에 왔을 때는 MIN 플레이어의 행동을 수행한다.
Alpha-beta Pruning
Alpha-beta Pruning이란?
그런데 지수적으로 증가하는 시간복잡도를 지닌 minimax search처럼 과연 모든 게임 트리의 노드를 탐색해야 할 필요가 있는지 의문이 들 수 있다. 트리를 타고 들어간 어느 순간부터는 더 이상 탐색하지 않아도 되는 경우가 존재하면 그때 해당 경로로 들어가는 탐색을 멈추고 다른 경로를 탐색해볼 수 있지 않을까? 이러한 의구심에서 나온 아이디어가 바로 alpha-beta pruning(알파 베타 가지치기)이다.
Alpha-beta pruning은 최선의 수를 두는 플레이어의 선택에 최종적으로 영향을 끼치지 않는 가지를 삭제하는 것이다. Alpha-beta pruning에 관한 자료를 찾아보면 복잡하게 설명이 되어 있는 경우가 있어서 이해하는데 고생했는데, 개인적으로 다음과 같이 정리하면 헷갈릴 일 없이 쉽게 이해할 수 있었다.
Alpha-beta Pruning의 아이디어
게임의 가정은 앞서 언급한 바처럼 게임이 종료되었을 때 가장 높은 점수를 얻은 플레이어가 승리하는 것이다.
먼저 alpha와 beta의 정의를 아래와 같이 하자.
- Alpha: 현재까지 내가 이기기 위해 찾은 최고 점수
- Beta: 현재까지 상대방이 나를 지게 만들기 위해 찾은 최저 점수
우리는 앞서 가정한 바처럼 게임에서 승리를 쟁취하기 위해 최선의 행동을 택할 것이지만, 상대방도 마찬가지로 최선의 행동을 택할 것이다. 그러면 만약 내가 게임을 이길 수 있는 어떤 경로를 찾았을 때, 이를 알고 있는 상대방이 과연 해당 경로로 가도록 가만히 보고만 있을까? 상대방은 해당 경로로 게임이 진행되지 않도록 최대한 노력해서 자신에게 가장 유리한 다른 방향으로 게임이 흘러가게끔 노력할 것이다. 반대로 생각해보자. 만약에 상대방이 나를 지게 만드는 불리한 경로를 찾았고 내가 해당 경로가 무엇인지를 알고 있으면, 나는 해당 경로로 게임이 흘러가도록 가만히 보고만 있을까? 그렇지 않다. 어떻게든 내게 가장 유리한 다른 방향으로 게임이 흘러가게끔 노력할 것이다. 물론 상대방이 찾은 내게 불리한 경로로만 갈 수밖에 없는 상황이면 어쩔 수 없이 그 경로로 게임이 흘러갈 수도 있겠지만, 그전에 최대한 다른 행동 또는 수를 찾아봄으로써 최대한 불리한 조건을 비켜 가도록 할 것이다. 상대방도 마찬가지이다. 상대방도 내가 상대방을 불리하게 만드는 경로로 빠지지 않도록 최대한 다른 방법을 찾을 것이다. 즉, 모든 플레이어는 각자에게 불리한 상황으로 빠지지 않도록 다른 방법을 찾으려고 하며, 이는 승리를 쟁취하기 위해 노력하는 플레이어에게 당연한 현상이다.
여기서 조금 더 나아가 보자. 내가 상대방을 불리하게 만드는 경로를 찾았는데 상대방이 해당 경로를 피할 수 있는 다른 경로를 이미 찾았으면 내가 찾은 경로와 연관된 노드를 타고 가면서 더 탐색할 필요가 있을까? 그렇지 않다. 어차피 상대방은 내가 찾은 경로를 선택하지 않을 것이고 자신이 찾은 최선의 경로를 택할 것이다. 그래서 더 이상 탐색하지 않고 해당 경로와 연관된 서브 트리를 가지치기 한다.
반대로 상대방이 나를 불리하게 만드는 경로를 찾았는데 내가 해당 경로를 피할 수 있는 다른 경로를 이미 찾았으면 내가 과연 상대방의 경로를 택할 일이 있을까? 전혀 없다. 나는 내게 맞는 최선의 선택을 할 테니까. 결국 더 이상 상대방은 해당 경로로 탐색할 이유가 없고 해당 경로와 관련된 서브트리를 가지치기 한다.
Alpha Cut-off와 Beta Cut-off
Alpha Cut-off
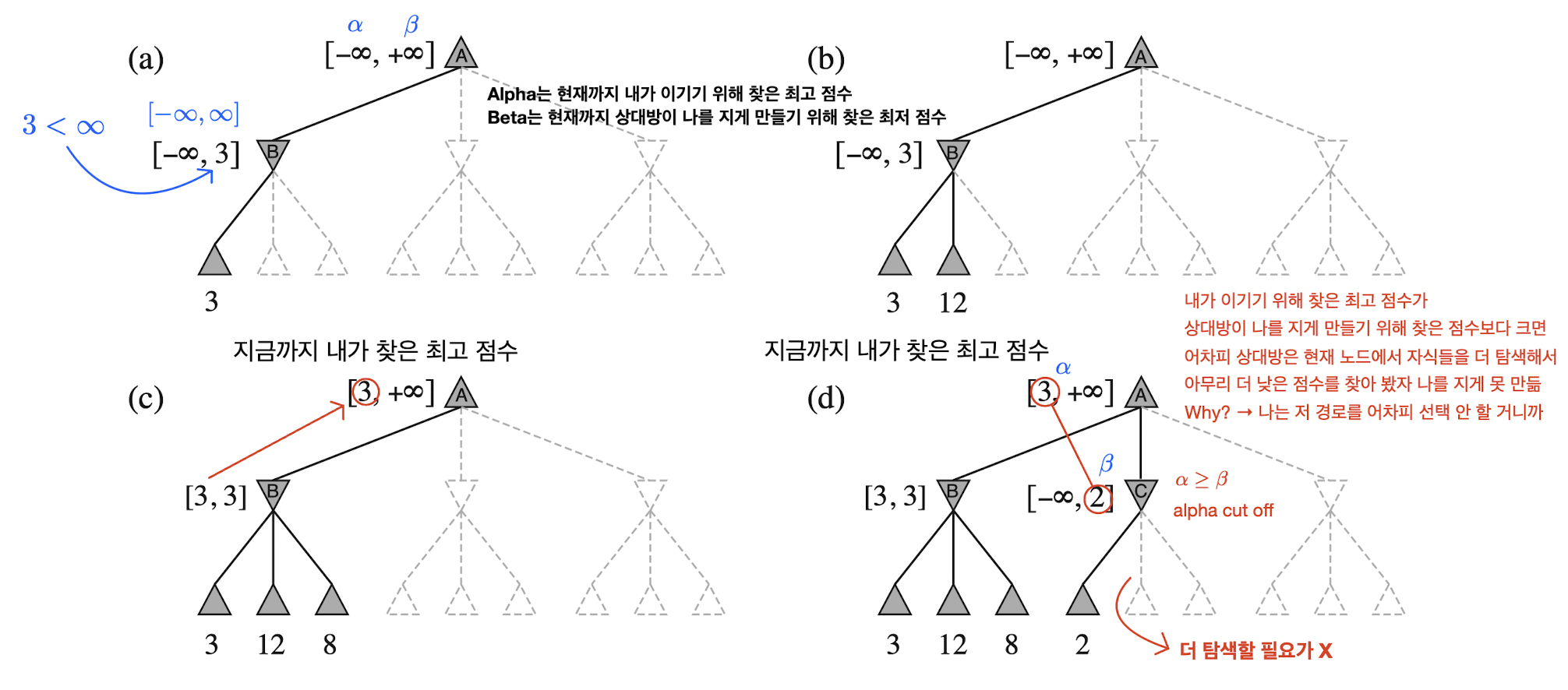
예시의 그림을 살펴보면 좀 더 쉽게 이해할 수 있다. (d)는 MAX 플레이어인 내가 이기기 위해 찾은 최고 점수가 MIN 플레이어인 상대방이 나를 지게 만들기 위해 찾은 점수보다 큰 상황이다. 나는 이전에 탐색한 자식에서 minimax-value가 3인 더 큰 점수의 경로를 이미 찾은 상태다. 그러면 어차피 상대방은 현재 노드인 C에서 자손을 더 탐색하면서 아무리 더 낮은 점수를 찾는다고 하더라도 나를 지게 만들지 못한다. 왜냐면 나는 이미 더 좋은 점수의 경로를 찾은 상황이니까 저 경로를 선택할 일이 없다. 그러므로 상대방은 C의 나머지 자손을 탐색할 필요가 없다. 다시 말해, 상대방이 더 탐색을 진행해서 2보다 작거나 같은 점수를 찾는다 하더라도 나는 그걸 절대 선택할 일이 없으니까 말이다.
- 상대방(
MIN): 너를 불리하게 만들 경로의 값인 2를 찾았어. 😜 - 나(
MAX): 어차피 난 이미 3을 갖는 경로를 찾아서 네가 찾은 경로는 절대 선택할 일이 없는데? 😂 - 상대방(
MIN): 하... 여기서는 더 탐색해 봤자 안 되겠네... 여기서 탐색 끝내자. 😮💨
수식으로 접근하면 이전에 탐색한 자식에서 찾은 minimax-value 값인 3이 바로 alpha이고, C 노드의 자손에서 상대방이 찾은 나를 불리하게 만드는 minimax-value 값인 2가 바로 beta이다. Alpha 값이 beta 값보다 크거나 같아서 더 이상 탐색을 할 필요가 없어 가지치기를 하는 걸 alpha cut-off이라고 한다.
Beta Cut-off
Alpha cut-off가 있으면 beta cut-off도 있다. 앞에서 설명한 내용과 플레이어의 상황만 서로 대치시키면 된다.
- 나(
MAX): 너를 불리하게 만들 경로를 찾았어. 😜 - 상대방(
MIN): 어차피 난 이미 내게 더 유리한 경로를 찾아서 네가 찾은 경로는 절대 선택할 일이 없는데? 😂 - 나(
MAX): 하... 여기서는 더 탐색해 봤자 안 되겠네... 여기서 탐색 끝내자. 😮💨
위의 내용으로도 설명할 수 있지만, MAX 플레이어의 관점으로 통일해서 생각하면 이해하기가 편하므로 다음과 같이 바꿔보자. MAX 플레이어인 나는 자신을 더 유리하게 만드는 경로를 택하지만, MIN 플레이어인 상대방은 최선을 다해 나를 더 불리하게 만들 경로를 택할 것이다.
- 나(
MAX): 나를 유리하게 만들 경로를 찾았어. 😜 - 상대방(
MIN): 어차피 난 이미 너를 더 불리하게 만들 경로를 찾아서 네가 찾은 경로는 절대 선택할 일이 없는데? 😂 - 나(
MAX): 하... 여기서는 더 탐색해 봤자 안 되겠네... 여기서 탐색 끝내자. 😮💨
구체적인 예시를 들어보자. MAX 플레이어인 내가 이기기 위해 찾은 최고 점수가 MIN 플레이어인 상대방이 나를 지게 만들기 위해 찾은 점수보다 큰 상황이다. 상대방은 이전에 탐색한 자식에서 minimax-value가 더 작은 점수의 경로를 이미 찾은 상태다. 그러면 어차피 나는 현재 노드에서 자손을 더 탐색하면서 아무리 더 높은 점수를 찾는다고 하더라도 상대방은 나를 지게 만들기 위해 내가 이기는 꼴을 만드는 경로를 택하지 않을 것이므로 나는 여기서 더 이상 탐색해봤자 내가 자신을 이기게끔 만들지 못한다. 왜냐면 상대방은 이미 나를 더 불리하게 만들 경로를 찾은 상황이니까 현재 노드에서 내가 찾은 경로를 선택할 일이 없다. 그러므로 나는 현재 노드에서 나머지 자손을 탐색할 필요가 없다. 즉, 내가 현재 노드에서 더 탐색을 진행해서 같거나 더 높은 점수의 경로를 찾는다고 하더라도, 나를 지게 만들 상대방은 내가 찾은 경로를 절대 선택할 일이 없으니까 말이다.
매우 나이브하게 생각해 보면 남이 좋아지는 꼴 보면 배가 아파서 남 잘 되지 못하도록 하는 방법을 모색하는 플레이어라고 볼 수도 있겠다... 🙄
Alpha-beta Pruning의 알고리즘
Alpha-beta pruning 알고리즘을 pseudo code로 살펴보면 다음과 같다.

Minimax search와 마찬가지로 MAX-VALUE와 MIN-VALUE에서 각각 MAX와 MIN 플레이어가 최선의 행동을 택하는데, MAX 플레이어는 가장 높은 minimax value를 찾고 MIN 플레이어는 가장 낮은 minimax value를 찾을 것이다. 대신 플레이어마다 각 노드에서 탐색한 자식의 minimax value를 봤을 때 더 탐색할 이유가 없다고 판단되면 현재 노드의 자손에 관한 탐색을 종료한다. 이 판단 조건이 위의 코드에서 MAX-VALUE의 $v \ge \beta$와 MIN-VALUE의 $v \le alpha$이다.
코드를 살펴보면 DFS(Depth-First Search)와 유사하지만 pruning 되는 조건을 고려헀을 때 어떠한 자식 노드부터 먼저 탐색하느냐가 중요하게 된다. 즉, pruning 되는 조건을 빨리 찾을 수 있는 순서로 자식 노드를 탐색을 해야 더 많은 나머지 경로를 가지치기 할 수 있는 가능성을 높일 수 있다. 최상의 순서로 자식 노드를 탐색하면 DFS의 $O(b^m)$인 시간복잡도를 $O(b^{m/2})$로 줄일 수 있다.
아래도 마찬가지로 픽맨 게임 프로젝트를 진행하면서 픽맨이 최선의 행동을 택하기 위해 alpah-beta pruning을 하는 코드를 작성한 것이다.
alpha = float("-inf")
beta = float("inf")
def is_terminal(gameState, currentDepth):
return gameState.isWin() or gameState.isLose()
def alpha_beta_search(gameState, depth, agent, alpha, beta):
# Pacman is an agent which number is 0
if is_terminal(gameState, depth):
return {'utility': self.utilityFunction(gameState), 'move': None}
agent = agent % gameState.getNumAgents()
if agent == 0:
return max_value(gameState, depth + 1, agent, alpha, beta)
else:
return min_value(gameState, depth, agent, alpha, beta)
def max_value(gameState, depth, agent, alpha, beta):
highest_value = float("-inf")
possible_moves = gameState.getLegalActions(agent)
best_move = None
for move in possible_moves:
successor = gameState.generateSuccessor(agent, move)
new_value = alpha_beta_search(successor, depth, agent + 1, alpha, beta)['utility']
if new_value > highest_value:
highest_value = new_value
best_move = move
alpha = max(alpha, highest_value)
if highest_value >= beta:
return {'utility': highest_value, 'move': move}
return {'utility': highest_value, 'move': best_move}
def min_value(gameState, depth, agent, alpha, beta):
lowest_value = float("inf")
possible_moves = gameState.getLegalActions(agent)
best_move = None
for move in possible_moves:
successor = gameState.generateSuccessor(agent, move)
new_value = alpha_beta_search(successor, depth, agent + 1, alpha, beta)['utility']
if new_value < lowest_value:
lowest_value = new_value
best_move = move
beta = min(beta, lowest_value)
if lowest_value <= alpha:
return {'utility': lowest_value, 'move': move}
return {'utility': lowest_value, 'move': best_move}
return alpha_beta_search(gameState, 0, 0, alpha, beta)['move']
Cut-off Test
Cut-off Test란?
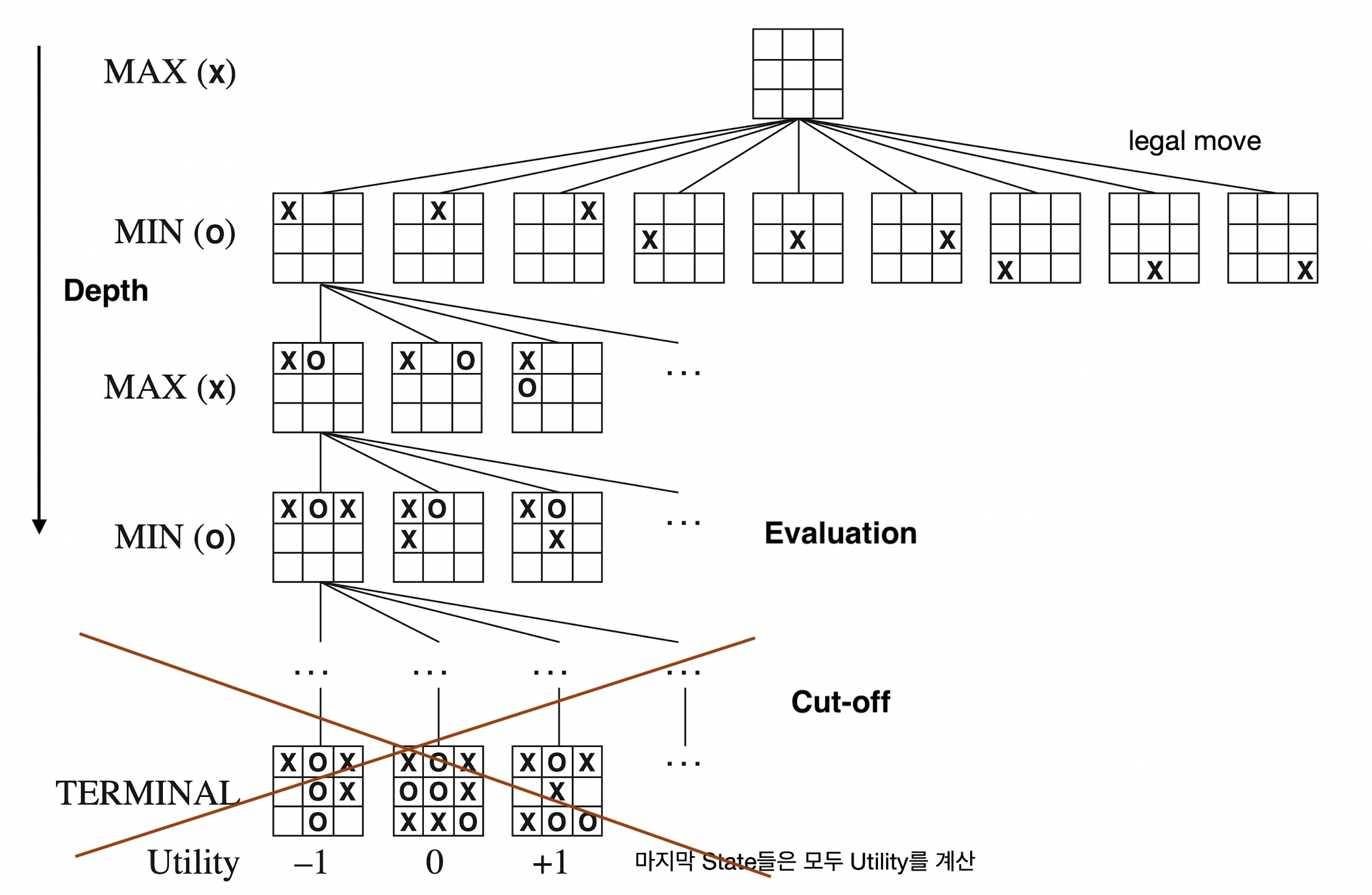
그러나 minimax search와 alpha-beta pruning 모두 시간복잡도가 exponential 하므로 좀 더 짧은 시간 내에 최선의 선택을 하기에는 좋지 않은 방법일 수도 있다. 이를 해결하기 위해 IDS(Iterative Deepening Search)의 아이디어처럼 어느 정도 정해진 깊이 이상 탐색하면 거기서 가지치기를 하고 대신 leaf node까지 탐색을 하지 못할 수 있으므로 해당 노드에서의 minimax value의 추정치를 반환하는 것이다.
Minimax search와 alpha-beta pruning에서는 게임의 종료 상태인 leaf node까지 도달한 후 거기서의 utility function 값을 찾지만, 일정 깊이 이상 탐색하고 cut-off를 하게 되면 leaf node에 도달하지 못할 수 있기에 추정치를 반환하므로 추정치를 잘 계산할 수 있는 evaluation function을 잘 정의하는 것이 중요하다. Evaluation function은 현재 cut-off한 노드의 상태에서 다양한 특징을 고려하여 정의할 수 있다.
Cut-off Test 예시
def cut_off_test(gameState, currentDepth):
return gameState.isWin() or gameState.isLose() or currentDepth == self.depth
앞서 살펴 본 팩맨 게임에 cut-off를 적용해 보면, 우리가 최대 보고자 하는 깊이를 self.depth를 정했을 때 cut off 조건을 판단하는 함수에서 현재 도달한 깊이가 self.depth와 같은지를 비교하는 구문을 추가할 수 있다.
if cut_off_test(gameState, depth):
return {'utility': self.evaluationFunction(gameState), 'move': None}
cut_off_test 함수에서 cut-off 조건을 만족하면 기존의 utilityFunction의 반환 값이 아니라 evaluationFunction의 반환 값을 반환한다.
출처
1. 서강대학교 CSE4185 기초인공지능 양지훈 교수님 수업
2. Stuart J. Russell, Third Edition, Artificial Intelligence: A Modern Approach
3. CS188 UC Berkeley Project 2 - Multi Agent Search (https://inst.eecs.berkeley.edu/~cs188/fa18/project2.html)
'AI > AI 기본' 카테고리의 다른 글
| Hidden Markov Model과 Filtering, Forwarding 그리고 Viterbi Algorithm (0) | 2023.04.13 |
|---|---|
| Transformer의 Multi-Head Attention과 Transformer에서 쓰인 다양한 기법 (4) | 2023.04.11 |
| Transformer를 사용하는 것이 항상 좋을까? (0) | 2022.08.31 |
| Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교 (0) | 2022.07.23 |
| Attention 기법을 사용한 Seq2Seq with Attention (0) | 2022.07.14 |
소중한 공감 감사합니다.