Bayesian Personalized Ranking(BPR)

 

2022년 3월 7일(월)부터 11일(금)까지 네이버 부스트캠프(boostcamp) AI Tech 강의를 들으면서 개인적으로 중요하다고 생각되거나 짚고 넘어가야 할 핵심 내용들만 간단하게 메모한 내용입니다. 틀리거나 설명이 부족한 내용이 있을 수 있으며, 이는 학습을 진행하면서 꾸준히 내용을 수정하거나 추가해 나갈 예정입니다.

 

 

Bayesian Personalized Ranking(BPR)

 

Personalized Ranking

하나의 사용자에게 순서가 있는 아이템 리스트를 제공하는 문제이며, 즉, 아이템 추천 문제로 귀결된다.

유저가 Item $i$보다 $j$를 좋아한다면 이 정보를 사용해 MF의 파라미터를 학습한다.

유저 $u$에 대해 item $i$ > item $j$라면 이는 유저 $u$의 Personalized Ranking으로 정의할 수 있다.

 

관측되지 않은 데이터에 관해서 두 가지를 고려해 볼 수 있다.

• 유저가 아이템에 관심이 없는지
• 유저가 실제로 관심이 있지만 아직 노출되지 않아서 모르는 것인지

 

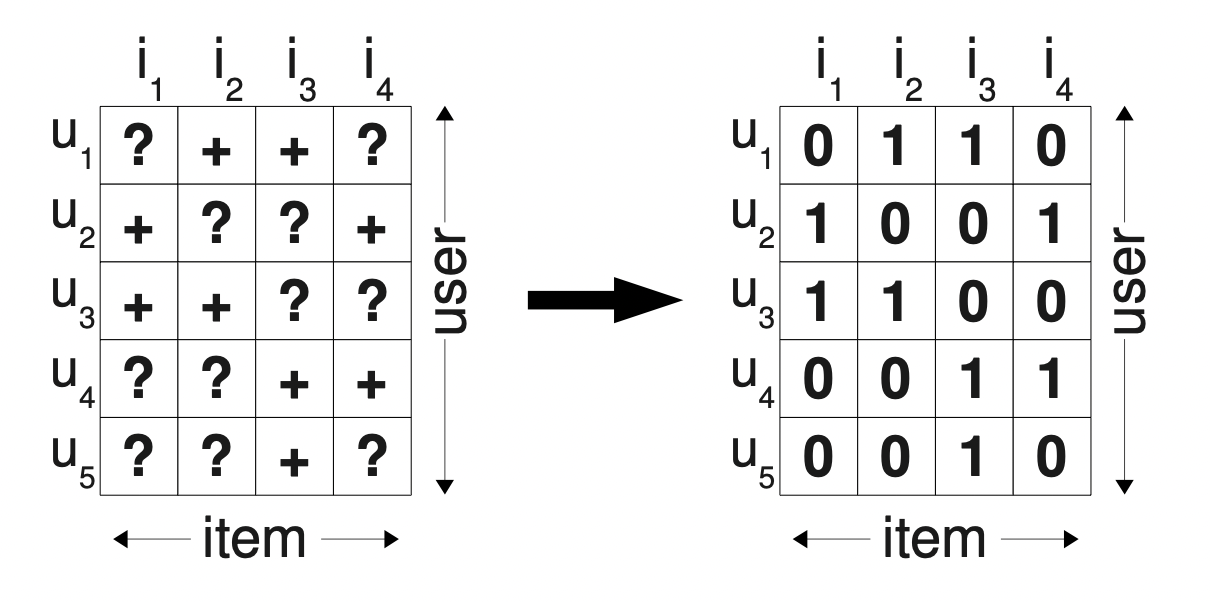
[출처] https://arxiv.org/pdf/1205.2618.pdf?source=post_page, BPR: Bayesian Personalized Ranking from Implicit Feedback

 

그래서 단순히 유저에게 관측된 아이템은 1로, 관측되지 않은 아이템은 0으로 값을 설정해버려민, 유저가 실제로 관심은 있지만 아직 노출되지 않은 아이템도 값이 0으로서 negative feedback으로 학습될 것이다.

 

이를 보완하여 BPR에서는 유저의 아이템에 대한 선호도 랭킹을 생성하여 이를 MF의 학습 데이터로 사용하는 것이 목적이며, 관측되지 않은 item에 관해서도 정보를 부여하여 학습하고 이에 관해서 ranking을 부여할 수 있는 특징이 있다.

 

우선 다음과 같이 가정을 해볼 수 있다.

• 관측된 item을 관측되지 않은 item보다 선호한다.
• 관측된 아이템끼리는 선호도를 추론할 수 없다.
• 관측되지 않은 아이템끼리도 선호도를 추론할 수 없다.

 

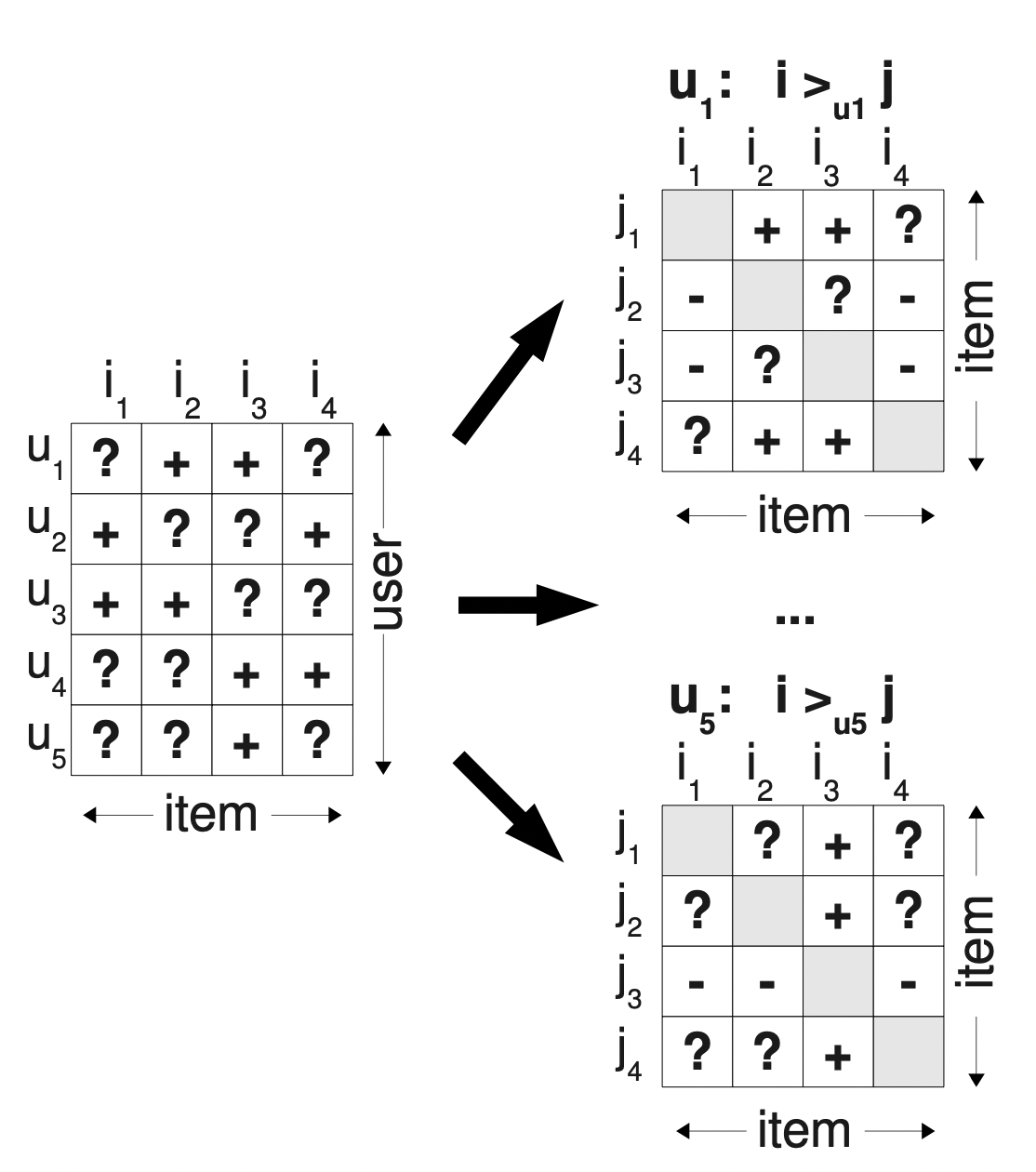
[출처] https://arxiv.org/pdf/1205.2618.pdf?source=post_page, BPR: Bayesian Personalized Ranking from Implicit Feedback

 

위의 규칙에 따라서 유저 $u$가 아이템 $i$를 $j$보다 선호하면 '+', 그렇지 않으면 '-', 선호도를 추론할 수 없으면 '?'가 된다.

 

유저의 아이템 선호도에 대한 학습 데이터를 생성한다.

유저 $u$가 선호하는 아이템, 즉 관측된 아이템들을 $I_u^+$라고 한다.

또한 유저가 선호하지 않은, 즉 관측되지 않은 아이템들을 $I \setminus I_u^+$라고 한다.

 

$$ D_S: = \{(u, i, j) | i \in I_u^+ \wedge j \in I \setminus I_u^+\} $$

 

 

최대 사후 확률 추정(Maximum A Posterior)

데이터에서 모델 파라미터를 학습하는 방법에는 MLE(Maximum Likelihood Estimation)와 MAP가 있다.

MAP는 사후 확률이 최대가 되는 파라미터를 구하는 것이다.

사후 확률($p(>_u)$)을 예측하기 위해 사전 확률과 가능도로 이를 추정하는 것이다.

 

• 사전 확률(prior): $p(\Theta)$, 파라미터에 대한 사전 정보
• 가능도(likelihood): $p(>_u|\Theta)$, 주어진 파라미터에 대한 유저의 선호 정보의 확률
• 사후확률(posterior): $p(\Theta| >_u)$, 주어진 유저의 선호 정보에 대한 파라미터의 확률

$$ p(\Theta | >_u) \propto p(>_u|\Theta) p(\Theta) $$

 

사후 확률을 최대화한다는 것은 주어진 유저 선호 정보를 최대한 잘 나타내는 파라미터를 추정하는 것이다.

모든 유저 선호 정보($>_u$)에 대한 likelihood는 다음과 같다.

 

$$ \underset{u \in U}{\prod} p(>_u|\Theta) = \underset{(u, i, j) \in D_S}{\prod} p(i>_u j | \Theta) = \underset{(u, i, j) \in D_S}{\prod} \sigma \big{(} \widehat{x_{u,i,j}}(\Theta) \big{)} $$

 

$p(i >_u j) := \sigma(\widehat{x_{u,i,j}}(\Theta))$

활성함수(sigmoid 함수) $\sigma(x) := \frac{1}{1 + e^{-x}}$

$\hat{r}_{u,i} = p_u^Tq_i$

$\hat{r}_{u,j} = p_u^Tq_j$

$\widehat{x_{u,i,j}} = \hat{r}_{u, i} - \hat{r}_{u, j} = p_u^T q_i - p_u^T q_j$

 

파라미터에 대한 사전확률($p(\Theta)$)은 정규 분포를 따른다고 가정한다.

학습하는 파라미터인 유저와 아이템 벡터는 모두 벡터 형태이므로 정규분포도 행렬의 형태로 정의해야 한다.

평균이 모두 0이고 공분산 행렬이 $\mathit{\Sigma_{\Theta}}$인 정규분포를 따른다고 가정하며,

공분산 행렬 $\mathit{\Sigma_{\Theta}}$는 $\lambda_{\Theta} I$로 설정하여 하이퍼 파라미터의 계수를 조정한다.

$$ p(\Theta) \sim N(0, \mathit{\Sigma_{\Theta}}) = N(0, \lambda_{\Theta} I) $$

$$ \begin{aligned} \text{BPR-Opt} :=& \ln p(\Theta| >_u)\\ =& \ln p(>_u|\Theta) p(\Theta)\\ =& \ln \underset{(u, i, j) \in D_S}{\prod} \sigma \big{(} \widehat{x_{uij}}(\Theta) \big{)} p(\Theta)\\ =& \underset{(u,i,j) \in D_S}{\sum} \ln \sigma \big{(} \widehat{x_{uij}}(\Theta) \big{)} + \ln p(\Theta)\\ =& \underset{(u,i,j) \in D_S}{\sum} \ln \sigma \big{(} \widehat{x_{uij}}(\Theta) \big{)} - \lambda_{\Theta} \|\Theta\|^2 \end{aligned} $$

 

목적함수인 BRP-Opt는 미분 가능하므로 Gradient Descent로 Optimization을 수행한다.

그러나 일반적인 Gradient Descent가 적절한 학습 방법은 아니다.

 

$$ \begin{aligned} \frac{\partial \text{BPR-Opt}}{\partial \Theta} :=& \ln p(\Theta| >_u)\\ =& \underset{(u,i,j) \in D_S}{\sum} \frac{\partial}{\partial \Theta }\ln \sigma \big{(} \widehat{x_{uij}}(\Theta) \big{)} - \frac{\partial}{\partial \Theta }\lambda_{\Theta} \|\Theta\|^2\\ \propto& \underset{(u,i,j) \in D_S}{\sum} \frac{-e^{-\hat{x}_{u,i,j}}}{1 + e^{-\hat{x}_{u,i,j}}} \cdot \frac{\partial}{\partial \Theta }\hat{x}_{u,i,j} - \lambda_{\Theta} \|\Theta\|\\ \end{aligned} $$

$$ \Theta \leftarrow \Theta - \alpha \frac{\partial \text{BPR-Opt}}{\partial \Theta} $$

 

 

LEARNBPR

Bootstrap 기반의 SGD를 사용하는 방식이다.

$$ D_S: = \{(u, i, j) | i \in I_u^+ \wedge j \in I \setminus I_u^+\} $$

 

일반적인 SGD를 사용하면 보통 i보다 j가 훨씬 많기 때문에 학습의 비대칭이 발생한다.

그래서 동일한 $u$, $i$에 대해 계속 업데이트가 되므로 수렴이 잘 되지 않는다.

그러나 triples 단위로 랜덤 샘플링하면 $i$와 $j$의 비대칭 학습이 해소될 수 있다.

동일한 $u$, $i$가 계속 등장하기 않기 때문에 성능이 우수하다.

 

유저 $u$의 벡터를 $p_u$, 아이템 $i$의 벡터를 $q_i$라고 하면

$\hat{r}_{u,i} = p_u^Tq_i$

$\hat{r}_{u,j} = p_u^Tq_j$

$\widehat{x_{u,i,j}} = \hat{r}_{u, i} - \hat{r}_{u, j} = p_u^T q_i - p_u^T q_j$

 

$$ \frac{\partial \hat{x}_{u,i,j}}{\partial \theta}= \begin{cases} (q_{ik} - q_{jk}), &\mbox{if } \theta = p_{uk} \\ p_{uk}, &\mbox{if } \theta = q_{ik}\\ -p_{uk}, &\mbox{if } \theta = q_{jk}\\ \end{cases} $$

 

 

BPR 과정 요약

1. Implicit Feedback 데이터만을 활용해 아이템 간의 선호도를 도출한다.
2. Maximum A Posterior 방법을 통해 파라미터를 최적화한다.
3. LEARNBPR이라는 Bootstrap 기반의 SGD를 활용해 파라미터를 업데이트한다.
4. Matrix Factorization에 BPR Optimization을 적용한 결과 추천 성능이 우수하다.