AI/Graphics

RenderNet: 3D shape를 가지고 differentiable rendering을 수행할 수 있는 Convolutional network

들어가기 전에

이번 논문 리뷰에서는 differentiable rendering을 CNN(Convolutional Neural Network)를 사용하여 shading effect, 3D shape reconstruction, novel-view synthesis task 등 다양한 graphics rendering 작업에 응용할 수 있는 가능성을 보여 준 RenderNet 논문에 관해 정리하고자 한다. 해당 논문을 선택한 이유는 CNN이라는 간단한 neural network를 사용하여 differentiable rendering을 수행한 점이고, rendering을 미분 가능하게 수행하기 위해 논문 저자가 어떠한 노력을 했는지 그 방법을 살펴 볼 필요가 있다고 생각해서다.

먼저 rendering이 정확히 무엇이고, 왜 rendering 분야에서 differentiable rendering에 그토록 주목하는지 그 배경을 알아볼 필요가 있다고 느꼈다.

렌더링(Rendering)이란?

[출처] https://commons.wikimedia.org/wiki/File:Rendering_equation_dA.png, AlesZita

어떤 대상(object)이 되는 mesh 또는 shape와 함께 texture, lighting, camera position 등 scene에 관해 주어진 설명(description)을 가지고 그에 대응되는 output 이미지를 생성하는 과정을 의미한다. 여기서 mesh는 polygon으로 구성된 어떤 하나의 3D object이며, shape을 찾거나 만드는 과정은 모델링(modeling)의 영역에 해당된다.

렌더링에서는 이러한 mesh 또는 shape가 투영시키는 공간이나 실제 2D 화면에서 어떻게 보일지를 구하는 과정이며, 정확히 말해서는 가상의 3D object—shape, pose, material, texture 등—와 이를 에워 감싸는 scene의 정보—light position, distribution, intensity 등—를 가지고 현실적이거나 style이 적용된 image를 만들어내는 과정이다.

앞서 말한 texture, lighting, camera position이 scene에 관한 파라미터(parameter)이며, 이 값들이 변화되었을 때 output이 어떻게 달라질지를 예상하고 이를 최대한 ground truth에 맞게 rendering 하는 것이 중요하다. 꼭 앞서 말한 파라미터뿐만이 아니라 object의 이동 경로, 형태 변화 등 다양한 것들이 파라미터에 포함될 수도 있다.

특히 3D 렌더링에서는 임의로 주어진 3D object와 scene에 관한 정보를 input으로 받아서 이를 2D 이미지의 output으로 내보내는 함수를 찾는 것이다. 반면에 2D 이미지를 input으로 받아 이에 대응되는 3D object와 scene을 output으로 구하는 과정은 inverse rendering으로 볼 수 있는데, 다시 말해 2D 이미지를 가지고 3D object와 scene의 정보와 같은 속성들을 추정하는 건 inverse rendering의 목표이다.

왜 렌더링에서 미분 가능성(differentiability)이 중요한가?

렌더링에서는 scene에 관한 파라미터가 달라졌을 때 그 output image가 어떻게 달라질지를 빠르게 계산할 수 있는 게 중요하다. 그런데 미분 가능한(differentiable) rendering function을 구할 수 있으면 그러한 파라미터에 관해 derivatives를 계산할 수 있어서 optimization 또는 학습 가능한 neural network에 통합시킬 수 있다. 기존에 perceptron 또는 neural network를 학습시킬 때 feed forwaring 방식으로 weight의 학습을 수행했던 것이 backpropagation이 등장한 이래로 weight의 derivative 또는 gradient descentf를 구하는 것으로 학습 과정이 바뀌었다. 마찬가지로 rendering에서 input으로 받는 파라미터의 derivative를 구할 수 있으면 neural network를 학습하는 방법과 유사하게 optimization을 수행할 수 있는 가능성을 얻게 된다.

그래서 렌더링에서 ML(Machine Learning) 또는 DL(Deep Learning)을 사용한다는 것은 어떠한 모델을 가지고 렌더링 과정을 학습하겠다는 의미이다. 일반적인 ML 학습 과정과 같이 어떤 3D scene의 input을 받아 모델을 통해 생성(creation)한 이미지가 실제 output 이미지와 유사해지게끔 하여 그 차이인 loss function의 gradient descent를 구해서 극소 또는 극대를 찾는다.

또한 rendering function의 미분 가능성은 컴퓨터 그래픽스의 응용처를 더 확대시킬 수 있다. Object의 이동 경로가 파라미터로 존재하고 이를 변화시켰을 때 object가 image 상에서 어떻게 변화할지를 예측해야 할 경우, rendering function 자체가 미분 가능하면 그 대상의 앞으로 어떠한 방향으로 얼만큼 이동할 것인지를 예상할 수 있게 된다. 예시로 로보틱스(robotics) 분야에서 로봇의 팔 또는 다리가 어떻게 움직일지를 예상하는 방식처럼 쓰일 수 있지 않을까?

이 글에서는 논문에 관해 일일이 상세하게 설명하기보다는 저자가 무엇을 말하고자 하는지 그 핵심과 이와 관련하여 알아두어야 할 배경지식 위주로 요약하여 정리하고자 하므로 논문에서 서술된 내용과 순서 또는 항목이 뒤바뀔 수 있는 점에 양해를 구한다.

배경지식(Background)

Rendering function을 미분 가능하도록 만들려는 시도

저자는 기존의 3D shape를 2D image로 만드는 절차적인 컴퓨터 그래픽스 렌더링 파이프라인이 고성능을 요구한다고 지적한다. 특히 렌더링 단계의 일부인 visibility computation처럼 불연속적인 연산이 미분이 불가능한 점이 렌더링 파라미터와 결과 이미지를 서로 명료하게 연관시키기 어렵다고 한다.

그래서 rendering function을 non-differentiable에서 differentiable로 바꾸기 위한 여러 시도가 있어 왔는데, 논문 연구 당시에 non-differentiable rendering function을 미분 가능한 렌더링(differentiable rendering)으로 구현하기 위해 크게 두 가지 방법이 사용되었다고 한다.

주어진 non-differentiable rendering function을 부드럽게 만들어(soften) surrogate gradient를 찾는 것이다.
Non-differentiable rendering function에서 실제 gradient는 아니지만 이와 유사한 differentiable rendering function을 원래 렌더링 함수에 근사시키는 것이다.

논문의 introduction에서 recent work를 소개하면서 간략히 그 방법들이 소개되는데, 구체적으로 미분 가능한 근사 렌더링 함수를 구하는 방법도 제안되었고 rasterization 연산을 위한 근사 gradient를 찾는 방법도 나왔다고 말하고 있다. 그리고 image-based reconstruction에서는 3D object를 실루엣 마스크를 투영시키는 differentiable projection을 object의 렌더링된 이미지의 surrogate로 사용하는 방법도 존재한다. 또 다른 방법으로는 normal, depth, silhouette map들마다 미분 가능한 projective function을 고안했으나, 각 함수마다 오직 정사영만을 다룰 수 있거나 아니면 더 많은 input 이미지를 요구한다는 단점이 있다. 그리고 이러한 projection은 reconstruction process에서 error signal을 생성하는 데 사용될 수 있다고 서술한다.

그러나 위에서 제시한 접근 방법들은 특정한 rendering style, input의 기하학적인 type, 또는 depth나 silhouette map과 같은 몇몇의 output format에 국한된다. 더 나아가 이러한 접근법들은 network architecture를 디자인하는 관점에서 바라보고 있지 않다는 단점이 있다. 또한 이러한 방법은 occlusion을 다룰 때 제한이 있는데, 여기서 occlusion은 어떠한 ray가 장애물에 의해 가려지는 현상을 의미한다. 또한 특정 rendering effect에만 국한되어 사용될 수 있는 문제가 있다.

최근의 ML에서는 network architecture가 다양한 task의 성능을 향상시키는 데 매우 중요한 역할을 하고 있다. 예를 들어, 분류 작업에서는 ResNet과 DenseNet이 성능에 있어서 중요한 공헌을 했고, 픽셀별로 어떠한 부분에 속하는지를 분류하는 segmentation 작업에서는 U-Net이 short-cut connection을 지님으로써 segmentation mask의 세부적인 level까지 성능을 끌어올렸다. 이러한 관점에서 이 논문에서는 rendering과 inverse rendering 작업에 적합한 neural network architecture를 설계하는 데 집중했다.

그래서 논문의 저자는 3D shape로부터 2D image를 렌더링할 수 있으면서 새로운 projection unit을 사용한 differentiable rendering convolutional network인 end-to-end로 학습 가능한 RenderNet을 소개하고 있다. RenderNet에서는 공간상의 occlusion이나 shading 연산이 자동으로 network에 인코딩되며, 논문에서 시행한 실험에 따르면 다양한 shader에 관해 RenderNet이 성공적으로 학습을 수행할 뿐만이 아니라 앞서 말한 바처럼 하나의 이미지로부터 shape, pose, lighting, texture 정보를 역으로 추정할 수 있는 inverse rendering 작업에도 사용할 수 있다고 한다.

렌더링의 대표적인 두 가지 방법

일반적으로 가장 유명한 두 가지 rendering 방법은 rasterization과 ray-tracing이다.

Rasterization은 vector graphics를 pixel pattern에 투영(projection)시킬 수 있는 transformation matrix를 구하는 과정이다. Shape를 polygon으로 만들어서 그 polygon을 pixel의 집합인 image로 투영시킨 후, 인접하거나 같은 ray 위에 존재하는 픽셀의 색상을 결정한다. 그러나 기하학적인 정보만을 고려하기 때문에 광원에 따른 texture를 픽셀별로 일일이 계산하기가 어려워진다. 그래서 secondary ray를 사용하여 광원을 추적해서 현재 어떠한 픽셀이 어떤 texture를 보여줄지를 구하는 방법이 ray-tracing이며, 물리적으로 광원에서부터 출발하여 물체에 반사되어 픽셀로 오는 ray를 추적하므로 physical-based model이라고도 한다.

Rasterization과 ray-tracing은 모두 빠른 성능과 realism을 모두 달성했지만, 앞서 말한 inverse graphics에 관해서는 적용하기가 어려워진다. 이 두 가지 방법은 어떤 한 point의 visibility를 계산하기 위해 z-buffering과 ray-object intersection 같은 방법들이 continuous하지 않고 discrete한 연산에 의존하여 non-differentiable하다는 특성을 지닌다. 이들을 컴퓨터 비전 task에서 non-differentiable renderer 그 자체로 다뤄도 되지만, 문제는 앞서 계속 반복한 것처럼 기존의 그래픽스 파이프라인에 따라 object 또는 scene의 파라미터를 역으로 추정해야 하는 inverse rendering에서 문제가 된다. 그래서 렌더링 파라미터의 변화와 렌더링된 이미지의 변화를 연관지을 수 있는 differentiable renderer가 컴퓨터 그래픽스 응용 분야에 있어서 저변을 넓혀줄 것이라고 기대하고 있다.

렌더링이 이루어지는 두 단계

일반적으로 렌더링의 과정은 크게 두 단계로 구성된다고 볼 수 있다.

object가 scene에 존재하는지 그렇지 않은지, 또는 object가 다른 object에 의해 가려지는지를 계산하는 visibility computation
그러한 object가 어떻게 보이는지(픽셀별로 색이 어떠한지)를 계산하는 shading computation

구체적으로 shading 단계는 polygon을 차지하는 각 픽셀의 색을 결정하는 과정이며, 크게 flat shading과 smooth shading으로 나눌 수 있다.

Flat shading은 polygon 당 하나의 face normal을 구하는 방식이고, smooth shading은 vertex normal을 사용하여 각 픽셀별로 색을 계산하는 방법이다. Flat shading은 polygon마다 그 안에 속해 있는 모든 픽셀의 색을 한 번에 계산하므로 계산량은 적을 수 있지만, 실제와 동떨어지거나 섬세한 색상 표현은 어려울 수 있다. 반면에 smooth shading은 모든 각 픽셀마다 색을 계산하므로 연산량은 증가할 수 밖에 없다.

특히 이 논문에서 실험에 사용한 shader 중 하나인 Phong shading은 polygon을 이루는 vertex normal을 보간(interpolate)하여 polygon 내의 각 픽셀별로 색을 계산하는 방식인데, RenderNet은 임의의 물체가 주어졌을 때 이러한 Phong shading에서도 원활히 수행 가능함을 보여줬다.

RenderNet 모델

논문의 figure에 나온 RenderNet의 전반적인 architecture

RenderNet의 핵심은 pixel-space regression loss를 사용하여 end-to-end로 학습 가능한 convolution layer로 이루어진 differentiable rendering을 수행할 수 있는 network이다. 원문을 그대로 직역하다보니 말이 부자연스러운데, 모델이 어떻게 구현되었는지와 실험 결과를 살펴보면 이해할 수 있을 것이다.

RenderNet에서는 rasterization 또는 ray tracing을 사용하여 생성될 수 있으며, 앞서 언급한 두 단계인 visibility computation과 shading computation을 모델에서 학습한다. (개인적으로 이 두 단계가 모델에서 각각 어떠한 부분에서 학습되는지 주목할 필요가 있다고 느꼈다.) 또한 RenderNet은 target 이미지와 모델이 생성한 output 사이의 pixel-space loss를 줄이는 방향으로 학습한다.

Input과 Rigid Body Transformation

논문의 저자는 camera position을 바꿔서 shape를 rotation 하는 것까지 CNN이 학습하는 것은 어렵다고 설명한다. 이는 rotation matrix 연산 자체가 매우 expensive한 작업이다. (2차원에서의 rotation matrix에서 $\theta$를 가지고 $\cos \theta$와 $\sin \theta$를 계산해야 하는데, 각 data point마다 이 $\theta$가 얼마인지까지 학습하는 게 그렇게 쉬운 일은 아니다.) 그래서 voxel grid 형태의 3D shape와 이와 관련된 camera position과 light position의 정보를 input으로 함께 받아서 rotation, scaling, translation 등 rigid body transformation을 직접 적용하여 고정된 특정 camera position에서 물체를 바라본 3D voxel data로 바꾼다. 또한 rotation 후 변환된 shape의 grid가 안 짤리도록 더 큰 grid에 임베딩시킨다. 이러한 과정을 저자는 논문에서 'not from scratch'라고 표현했는데, 이는 아무런 정보도 주어지지 않은 상태에서 CNN이 학습을 수행하는 게 아니라 임의의 3D shape grid를 사전에 정의된 grid에 의도된 pose로 바꿔서 input으로 넣었다는 뜻이다.

3D Convolution과 Projection Unit

논문의 저자는 앞서 말한 렌더링의 두 단계를 고려하여 RenderNet 모델을 구현했다. 3D convolution 레이어들을 통과한 후 그 결과를 reshaping하는 레이어와 1 $\times$ 1 크기의 convolution layer를 통과시키는 것과 같은 MLP 레이어로 이루어진 projection unit은 visibility를 계산하는 단계에 해당된다. 즉, 3D convolution 레이어 모듈에서는 전체 depth에 관해 visibility를 학습하고, projection unit은 3D convolution 모듈을 통과하여 나온 4D tensor인 $W \times H \times D \times C$의 3D shape 결과를 3D tensor인 $W \times H \times (D \cdot C)$의 2D feature map으로 project 시키는 역할을 한다. 구체적으로 3D convolution 레이어에서는 down pooling과 Prelu activation function을 사용했으며, projection unit의 reshaping layer에서는 depth와 channel을 합쳐서 2차원의 feature map인 output으로 만드는 과정을 수행한다. 논문에서는 이처럼 projection unit에서 3차원 shape에서 2차원 이미지로 투영시키는 과정을 다음과 같은 식으로 나타냈다.

$$ I_{i,j,k} = f \left( \sum_{dc} w_{k, dc} \cdot V'_{i,j,dc} + b_k \right) $$

논문에서는 3D convolution 모듈의 output인 $32 \times 32 \times 32 \times 16$ tensor를 projection unit의 input으로 받아서 reshaping layer에서 $32 \times 32 \times (32 \cdot 16)$ tensor로 만들고, 이를 MLP에 통과시켜 $32 \times 32 \times 512$ tensor를 output으로 내보낸다.

2D Convolution

이후 projection unit의 output을 2D convolution 레이어 모듈의 input으로 넣는데, 이 2D convolution 모듈에서는 2D 이미지의 shading을 연산하는 과정을 수행한다. 이를 통과한 output은 크기 3의 channel을 갖는 $512 \times 512 \times 3$의 normal map이다.

RenderNet의 확장 가능성

논문의 저자는 RenderNet을 다른 네트워크의 결합시켜 더 많은 렌더링 파라미터를 다루거나 shadow rendering이나 texture mapping 같은 더 복잡한 작업을 수행할 수 있다고 말한다. 만약 앞서 설명한 Phong shading을 수행하기 위해 Phong illumination model을 결합시킨다고 하면 normal map 형태로 나온 normal vector $\vec{n}$와 light direction vector $\vec{l}$, 그리고 ambient constant $\vec{a}$를 사용하여 각 픽셀별로 shading $S$를 계산하고, 이를 albedo map $A$(광학적 특성을 제외하고 완전히 물체의 표면의 색만 표현하는 texture)와 결합시켜 최종적인 이미지를 만들 수 있다고 한다. 즉, RenderNet은 다양한 shader를 RenderNet이라는 하나의 네트워크로 합칠 수 있는 잠재력을 지니고 있다.

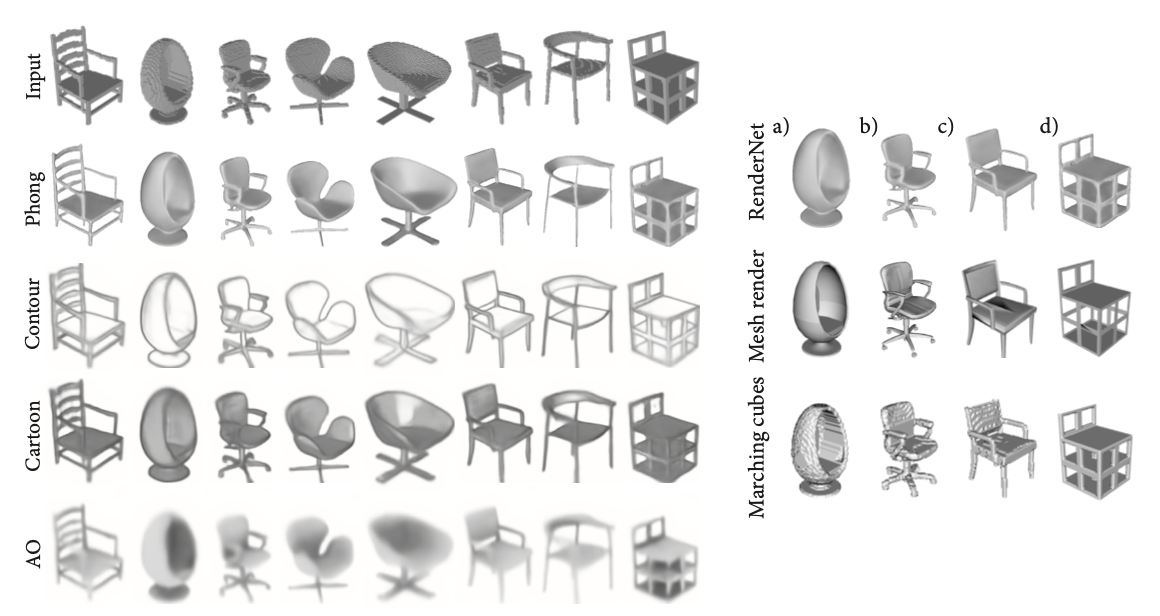
$$ \begin{align} S &= \max(0, \vec{l} \cdot \vec{n} + a)\\ I &= A \odot S \end{align} $$

위의 figure는 input으로 온 object에 Phong shader 뿐만이 아니라 다양한 shader(contour, cartoon, ambient occlusion)를 적용했을 때 나온 실험 결과이다. 오른쪽 사진은 RenderNet과 다른 모델에 관해 Phong shading을 적용했을 때의 결과를 비교한 모습인데, mesh artifacts를 겪지 않는 것으로 확인된다.

또한 논문의 저자는 RenderNet이 이제까지 학습하지 않은 category에 관해서도 좋은 일반화 성능을 보이는 것을 확인했다. 게다가 50% random noise가 있는 데이터가 주어지거나 입력에서 50%로 downsampling 된 데이터에 관해서도 그럴 듯한 렌더링 성능을 보인다고 한다. 이는 기존의 컴퓨터 그래픽스의 mesh rendering이 깨끗하고 높은 품질의 mesh를 필요로 한다는 점과 비교했을 때 확실한 이점이라고 볼 수 있다.

위의 figure에서 왼쪽의 토끼 모양의 grid 입력에 shader를 적용한 실험 결과가 이를 뒷받침해주며, 오른쪽의 원숭이 grid 입력을 다양한 각도에서 바라봤을 때 어떻게 보여질지를 렌더링하는 결과도 꽤 그럴 듯하게 나온 것을 볼 수 있다.

Encoder-decoder Architecture와의 비교

논문의 저자는 RenderNet을 encoder-decoder architecture 기반의 두 개의 다른 모델(EC와 EC-Deep)과 성능을 비교해보는 실험을 진행했다. 논문의 figure에서는 novel-view synthesis, relighting, 그리고 generalization task 수행 결과를 비교하여 보여준다. EC 모델들은 대상에서 중요한 부분의 디테일을 생성하는 데 실패해서 많이 뭉개져 보이는 것과는 다르게 RenderNet는 그렇지 않음을 확인할 수 있다.

위의 figure의 오른쪽에서 다른 모델과의 Phong Shader 비교 실험에서 PSNR(Peak Signal-to-Noise Ratio) 수치를 보면 RenderNet이 다른 모델보다 더 높다. 여기서 PSNR은 이미지의 화질의 손실 정보가 어떠한지를 측정하는 지표이며, 값이 크면 클수록 손실이 적고 화질이 좋다.

RenderNet의 Shape Reconstruction

저자는 RenderNet이 단일 이미지를 reconstruction 할 수 있는 inverse rendering을 수행하는 데도 사용될 수 있다고 말한다. 즉, 어떠한 2D 이미지에 관해 3D 상에서의 shape, pose, lighting과 같은 정보를 역으로 찾는 데 optimization을 사용할 수 있다고 설명한다. 다음과 같은 reconstruction loss를 최소화하는 방향으로 optimization을 반복하여 수행하면 달성할 수 있다고 판단했다.

$$ \underset{z, \theta, \phi, \eta}{\text{minimize}} \; \| I - f(z, \theta, \phi, \eta)\|^2 $$

여기서 $I$는 관찰된 이미지(ground truth), $f$는 기학습된 RenderNet, $z$는 reconstruct 해야 하는 shape, $\theta$와 $\eta$는 각각 pose와 lighting과 관련된 파라미터, 그리고 $\phi$는 texture 변수이다.

그러나 이 loss를 직접적으로 최소화하게 되면 noise가 있고 불안정한 결과를 내보낼 수 있다고 한다. 그래서 이를 해결하려는 시도로서 앞서 말한 과정을 정규화하기 위한 shape prior를 사용했다. 여기서 shape prior는 TL-embedding 네트워크와 유사한 기학습된 3D auto-encoder라고 한다. 그래서 $z$ 자체를 optimization 하는 대신에 latent representation인 $z'$를 최적화하는 방법을 택했다.

$$ \underset{z', \theta, \phi', \eta}{\text{minimize}} \; \| I - f(g(z'), \theta, h(\phi'), \eta)\|^2 $$

$g$는 방금 언급한 3D auto-encoder의 decoder인데, 이는 이미 decoder에서 학습한 prior shape 지식을 사용하여 $g(z')$를 정규화하는 데 사용된다. 또한 $h$도 decoder인데, 3D auto-encoder의 decoder 부분은 아니고 앞서 실험 관련하여 설명하면서 말한 texture rendering task에 관해 학습된 RenderNet을 decoder로 사용한 것이다. 이도 마찬가지로 texture 변수인 $\phi'$를 정규화하기 위해 사용된다. 이는 MAP(Maximum A Posterior) estimation의 관점에서도 해석할 수 있는데, shape decoder 부분이 기학습되어서 이미 알고 있는 사전 지식에 해당되는 prior term이고, likelihood term은 RenderNet에 의해 주어진다고 볼 수 있다.

논문의 저자는 reconstruction 결과에 관해 RenderNet과 DC-IGN을 비교하여 설명하고 있다. DC-IGN는 input 이미지로부터 요소들을 분해하여 latent space에서 shape, pose, lighting을 latent variable로 지니고, 이 latent space에 있는 정보들을 가지고 다시 이미지를 복원시키는 과정을 거친다. 반면에 RenderNet에서는 latent space에서 따로 분해하여 저장하지 않고 명백하게 3D geometry, pose, lighting, texture 정보를 가지고 reconstruction을 수행하므로 out-of-plane roation에서 향상된 결과를 얻을 수 있고, re-texturing도 적용할 수 있다.

이는 DC-IGN과 RenderNet에 관해 사람 얼굴 단일 이미지를 가지고 shape reconstruction을 수행한 결과를 보면 알 수 있다. DC-IGN에서는 texture를 네트워크에서 학습하지 못하므로 격자로 제외했다.

느낀 점

그동안 자연어 처리 분야의 추천시스템만 공부하다가 갑자기 방향을 틀어서 computer vision과 computer graphics 분야에 처음 진입해 공부하다보니 배경지식이 많이 부족하다는 생각이 들었다. 그리고 아직까지 rendering 관련 분야의 논문을 충분히 리뷰하지 못한 상태여서 최신 트렌드를 따라가는 건 둘째치고 이전에 학자들이 연구했던 시도에 관한 이해가 필요할 것 같다고 느꼈다.

Rendering function의 미분 가능성을 어떻게 직관적으로 판단해야 하는지 잘 모르겠다. 고등학교 수학 시간에는 '연속된 부드러운 곡선을 이루면 미분 가능하다'는 아이디어로 정말 나이브하게 생각했고, 수학적으로 접근하면 미분의 정의를 이용해서 어떤 지점에서 미분이 불가능한지를 고려하여 그 함수의 미분 가능성을 판단했다. 그런데 rendering function이 수식적으로 주어진 게 아닌 상황에서 그 렌더링 방법론만을 이해한 채 해당 rendering function이 미분 가능하다 또는 미분 불가능하다를 직관적으로 판단할 수 있는지 궁금해졌다. 아직 모르는 게 너무 많고 질문 자체가 너무 바보같기는 하지만, 논문이나 미팅 시간에 오가는 내용을 들어보면 그 미분 가능성을 판단하는 게 굉장히 중요한 것 같은데, 그 미분 가능성을 판단하는 방법 또는 기준을 어떻게 확인할 수 있는 것인지 알아봐야겠다.

→ 직관적으로 rendering function이 미분 가능하다는 걸 바로 이해한다는 건 사실 불가능하고, 논문에서 object에 관한 파라미터가 주어졌을 때 optimization을 위해 필요한 deterministic한 loss function이 이러한 파라미터에 관해 미분 가능한 함수로 정의되는지를 확인해야 한다. 단지 논문에서 어떤 한 모델에 관해 '미분 가능하다', '미분 불가능하다'라고 간단히 요약하고 넘어가는 것은 그 모델에서 관한 배경지식이 부족하거나 그 모델이 제안된 논문을 공부하지 않아서 그런 것으로 이해했다.

2020년에 NeRF가 발표된 이후 NeRF가 거의 3D reconstruction 분야에 한 획을 그었다고 한다. NeRF는 위치 정보와 ray 방향을 input으로 받아서 density와 color를 output으로 내는 MLP layer로 구성된 network를 사용했다고 한다. 다음 논문 리뷰에서는 NeRF에 관해 공부하여 정리할 예정이다.

출처
1. https://arxiv.org/abs/1806.06575
2. Intelligence Education Vietnam, CoTAI-Talk2: Thu Nguyen-Phuoc. Part 2.1 ~ 2.6: RenderNet and HoloGAN, https://www.youtube.com/watch?v=87GwMwLm7pQ&t=2s

저작자표시

Contents

새소식