Embarrassingly Shallow Autoencoders for Sparse Data: EASE 모델이 희소 데이터에 강한 이유
- -
Introduction
한 달이라는 긴 시간동안 네이버 부스트캠프 AI Tech 3기에서 진행했던 Movielens 데이터 기반의 영화 추천 대회 프로젝트가 마무리되었다. 팀원들과 밤낮으로 회의하면서 어떠한 모델을 사용하는 게 좋을지 고민했었는데, 순차 데이터보다는 좀 더 일반적인 데이터에 강한 autoencoder 기반의 여러 모델을 중심으로 앙상블한 것을 바탕으로 inference 결과를 제출했다.
그중에서 EASE(Embarrassingly Shallow Autoencoders for Sparse Data, ESAE)라는 모델이 매우 신기했는데, 다른 autoencoder 기반의 모델보다 상대적으로 성능이 좋을 뿐더러 매우 짧은 실행 시간을 가지는 특징을 지닌다. Hidden layer이 존재하지 않아 학습 파라미터의 수가 한 개로 매우 작다는 것도 눈여겨 볼 만하다.
사실 EASE를 대회에서 시도해 본 것도 EASE 모델 자체가 sparse한 데이터와 cold start problem에 강해서 특히 Million Song Dataset에서 다른 모델보다 압도적으로 좋은 성능을 보인다는 글을 보고 적용한 것인데, 예상보다 성능이 매우 좋게 나와서 팀원들 사이에서 놀랍다는 반응이 많이 나왔다. 실제로 paperswithcode.com에 올라온 평가 지표 결과를 봐도 EASE가 우수한 성능을 낸다는 걸 볼 수 있다.
[Million Song Dataset을 기반으로 평가한 모델 성능 비교]
https://paperswithcode.com/sota/collaborative-filtering-on-million-song
Papers with Code - Million Song Dataset Benchmark (Recommendation Systems)
The current state-of-the-art on Million Song Dataset is EASE. See a full comparison of 6 papers with code.
paperswithcode.com
Million Song Dataset에서는 EASE가 RecVAE보다도 압도적인 성능을 보인다.
[Movielens 20M을 기반으로 평가한 모델 성능 비교]
https://paperswithcode.com/sota/collaborative-filtering-on-movielens-20m
Papers with Code - MovieLens 20M Benchmark (Recommendation Systems)
The current state-of-the-art on MovieLens 20M is VASP. See a full comparison of 15 papers with code.
paperswithcode.com
Movielens 20M에서는 EASE가 H+Vamp Gated, RecVAE 등 다른 SOTA 모델보다는 성능이 좋지 못한 것으로 나오지만, 이번 대회에서는 Movielens 20M에 무작위로 마스킹을 하여 데이터가 더 희소해지면서 cold start problem 현상이 생겨서 EASE 단일 모델 성능이 RecVAE, H+Vamp Gated보다도 더 좋은 성능을 냈다. 여기서 cold start problem이란 어떤 유저의 활동 이력이 충분치 않아서 해당 유저에게 적절한 새로운 아이템을 추천하기 어려운 현상을 의미한다.
그런데 왜 EASE는 딥 러닝 모델이라고 보기 힘든 단순한 모델임에도 불구하고 희소 데이터에서 두드러지는 모습을 보이는지 궁금했다. 대회를 진행할 때는 시간에 쫒겨서 모델 자체를 제대로 분석하지 못했는데, 대회도 끝난 겸 궁금증을 참고만 있을 수가 없어서 이 모델이 소개된 다음 논문을 공부해봤다.
EASE(Embarrassingly Shallow Autoencoders for Sparse Data, ESAE)란?
모델명에서 shallow는 어떤 의미인가?
추천 시스템 논문을 보면 모델명에 모델의 특징이 포함되어 있는 경우가 종종 있다. 이 모델도 마찬가지로 이름을 직역하면 희소한 데이터를 위한 당황스러울 정도로 얕은 Autoencoders인데, 여기서 'embarrassingly shallow'는 것은 hidden layer가 존재하지 않는 선형 모델임을 의미한다. ('shallow' 자체에 관해서만 정확히 말하자면, hideen layer가 1개이거나 매우적은 모델을 shallow라고 말할 수 있을 것이다.)
일반적으로 autoencoder는 input 데이터를 encoder layer에 통과시켜서 latent space로 보내고, 이를 다시 decoder layer에 통과시켜서 재생성된 output이 얼마나 input과 유사한지를 비교하면서 학습을 진행한다. 그래서 autoencoder 기반의 모델에서는 encoder와 decoder라는 hidden layer가 존재한다. 이는 encoder layer에 input 데이터를 통과시켜서 나오는 latent space의 샘플링 분포의 모수인 평균과 분산을 추출하는 variational autoencoder 기반의 생성 모델에서도 마찬가지이다.
반면에 ESAE에서는 hidden layer를 필요로 하지 않아서 모델이 굉장히 단순하다. 실제로 모델 코드를 보면 다소 어이가 없을 정도로 간단하다. 논문에서는 이 모델의 별칭을 EASE로 사용하는데, 개인적으로 저자가 아마 이러한 특징을 노리고 이 모델의 약자인 ESAE를 역순으로 해서 '쉽다'는 의미의 EASE로 재치있게 이름을 붙인 게 아닌가 싶다.
그렇다고 Autoencoder은 아니다
이 논문에서 모델 이름에 autoencoder를 넣은 이유를 다음과 같이 설명하고 있다.
This is done by reproducing the input as its output, as is typical for autoencoders. We hence named it Embarrassingly Shallow AutoEncoder.
EASE는 input으로 받은 데이터가 어떠한 함수를 거쳐서 재생성된 output으로 나온다는 점에서 autoencoder와 유사하지만, 사실 엄밀히 말하면 autoencoder가 아니다.
EASE에서는 autoencoder와는 달리 input data를 latent space로 보내서 latent factor를 얻는 과정을 거치지 않지만, 단지 input 데이터가 output 데이터로 재생성된다는 점이 autoencoder과 닮아 있다. 즉, autoencoder와 닮아 있는 점이라고는 multi-hot vector로 이루어진 행렬 입력 데이터를 모델에 넣고 이를 출력 데이터로 재생성하여 원래의 입력 데이터와 loss를 비교하는 과정일 뿐이며, 정확히는 autoencoder 기반 모델이 아니다.
EASE의 특징
세 가지로 요약한 특징
논문에서 소개된 EASE의 특징을 세 가지로 요약하자면 다음과 같다.
- Hidden layer가 없다.
- Convex한 목적함수가 closed form solution이다.
- 학습 파라미터의 대각 성분이 0이다.
Hidden layer가 없다는 것은 앞에서 여러 번 언급되었지만, 목적함수가 closed form solution이라는 말은 잘 이해가 가지 않았다. 딥러닝에서는 이처럼 'closed form'이라는 말이 자주 등장하는데, closed form이 무엇인지 알아보았다.
Closed form(닫힌 형태)이란?
쉽게 말해 유한개의 방정식을 사용하여 어떠한 해를 해석적(analytic)으로 표현할 수 있는 종류의 문제를 의미하며, 간단하게 $x$를 해라고 할 때 "$x = \dots$ " 꼴처럼 나타낼 수 있는 문제을 뜻한다.
일반적으로 딥 러닝에서 목적함수를 통해 파라미터를 최적화 할 때는 관측해야 할 파라미터가 많아서 닫힌 형태로 정의되지 않는 경우가 많다. 그래서 목적함수를 미분하여 극대, 극소 등 임계점을 구하기가 어려워진다. 그래서 목적함수의 gradient를 구해서 해당 방향으로 이동하도록 파라미터를 업데이트하면서 극대 또는 극소에 도달하고자 하는 것이다.
그러나 EASE에서는 학습 파라미터의 최적해가 간단한 식으로 표현되는 closed form solution을 띤다. 그래서 EASE를 학습시키는 데 있어서 걸리는 wall-clock time이 Slim 모델을 학습시킬 때보다 몇 배로 더 적게 들 수 있다고 논문에서 말하고 있다. 여기서 wall-clock time은 실제로 모델이 학습하는 데 걸린 시간에 관해 사용자가 인지하기까지의 시간을 뜻한다.
EASE는 어떻게 학습할까?
입력 데이터 $X$
입력 데이터 행렬인 $X$는 아이템과 유저에 대한 implicit feedback인 interaction matrix이며, $X \in \mathbb{R}^{|U| \times |I|}$를 만족한다.
각 유저별로 어떠한 아이템을 클릭 또는 구매했는지에 관한 정보가 0 또는 1인 값으로 표현되어 있는데, positive feedback이 1의 값을 지닌다.
예를 들어, 다음과 같이 A, B, C 유저별로 a, b, c, d 아이템을 클릭한 데이터를 바탕으로 $X$ 행렬을 만들어 보면 다음과 같다.
| 아이템 a | 아이템 b | 아이템 c | 아이템 d | |
|---|---|---|---|---|
| 유저 A | 0 | 1 | 1 | 0 |
| 유저 B | 1 | 0 | 1 | 1 |
| 유저 C | 0 | 0 | 0 | 1 |
학습 파라미터 $B$
앞서 말했듯이 EASE는 학습 파라미터가 한 개밖에 없는데, 이 학습 파라미터 $B$는 아이템 간 아이템의 가중치 행렬로서 $B \in \mathbb{R}^{|I| \times |I|}$를 만족한다.
이를 입력 데이터 $X$와 행렬 곱을 해줌으로써 나온 결과가 원래 $X$와 얼마나 유사한지를 보면서 $B$를 학습해 나가는 것이다.
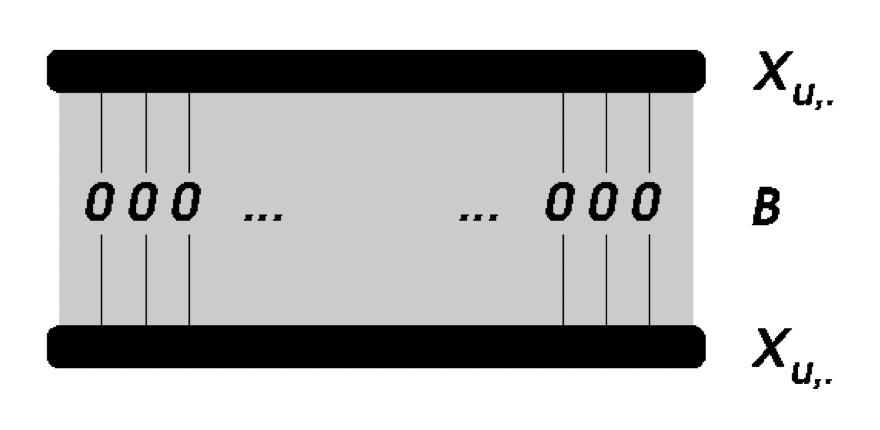
The self-similarity of each item is constrained to zero between the input and output layers.
논문에서도 여러 번 강조되지만 여기서 주의할 점은 $B$의 대각 성분이 0이어야 한다는 것이다.
이는 목적함수에서도 다루겠지만, 결국 $B$의 대각 성분을 0으로 한다는 제약 사항이 없으면 $B$가 단위행렬 $I$가 되어버려서 결국 $X$에 학습된 파라미터인 $B$가 아니라 단위행렬 $I$를 곱해버리는 의도치 않는 현상이 발생해버리기 떄문이다.
$B$의 대각 성분을 0으로 한다는 제약 사항을 가지고 라그랑주 승수법을 적용하여 closed form solution을 해결하는데, 이는 뒤에서 다룰 것이다.
출력 데이터 $S$
우리는 유저 $u$가 아이템 $i$에 관심이 있을 확률을 구해야 하는 것이 목표이므로, 입력 데이터 $X$에 학습 파라미터 $B$를 곱한 값을 모델이 예측한 ranking 점수로 활용한다. 이를 식으로 정리하면 다음과 같다.
목적함수
파라미터 $B$를 학습시키기 위한 목적함수가 존재해야 하는데, 이는 논문에서 다음과 같이 정의하고 있다.
$X$와 $XB$의 차이를 가장 작게 하는 $B$를 구하고 싶은 게 목표인데, 대신에 과적합을 예방하기 위한 L2-norm정규화 항인 $\lambda \cdot \|B\|_F^2$이 더해진다. 그래서 EASE 모델에서는 하이퍼파라미터(hyperparamter)도 $\lambda$ 하나 밖에 존재하지 않는다.
논문에서는 closed-form solution을 만족하기 위해 $X$와 $XB$의 차이를 계산하는 함수로서 square loss에 속하는 Frobenius norm을 사용했다. Frobenius norm는 쉽게 말해서 행렬 버전의 L2-norm이자 유클리디안 거리라고 생각해도 좋다.
그런데 multinomial likelihood와 같은 다른 손실함수를 사용하면 ranking의 정확도가 향상될 수도 있다고 첨언했는데, 이번 대회에서 square loss 대신에 다른 손실함수를 썼으면 점수가 더 오를 수 있지 않았을까 하는 아쉬움이 들었다.
목적함수를 최적화 하는 해 찾기
일반적인 딥 러닝 모델이라면 $B$를 파라미터로 지정해서 모델에 입력 데이터 $X$가 들어왔을 때 저 목적함수이자 손실함수인 식의 계산 결과를 반환해주면 된다. 그러면 역전파 알고리즘을 통해 이 loss를 최소화하는 gradient를 찾을 것이고, optimizer를 통해 gradient 방향으로 파라미터 $B$를 업데이트 해주면 된다. 대신에 $B$의 대각성분이 0이어야 한다는 조건을 만족해야 하므로 목적함수 뒤에 제약 사항을 반영한 항을 추가해준다. 코드로 살펴보자.
import torch
class EASE(nn.Module):
def __init__(self, n_items, lambda1, lambda2):
super(EASE, self).__init__()
self.B = torch.nn.Parameter(torch.Tensor(n_items, n_items))
self.lambda1 = lambda1
self.lambda2 = lambda2
def forward(self, X):
recon_matrix = X @ self.B # X와 B 행렬곱으로 재생성된 X'
loss = X.sub(recon_matrix)
loss = loss ** 2
loss = loss.sum()
regularization = torch.norm(self.B)
constraint = torch.sum((torch.diag(self.B) - 0) ** 2)
return loss + self.lambda1 * regularization + self.lambda2 * constraint
하지만 이럴 경우 보통 일반적인 딥 러닝 모델과 다르지 않아 효율이 떨어지고 학습 시간은 늘어날 수밖에 없다. 그래서 논문 저자는 closed-form solution을 제시하여 목적함수를 최소화 하는 해를 찾는 문제를 최적화 하는 방법을 제시했다.

논문에서 위에서 정의한 $B$의 대각성분이 0이어야 한다는 제약 사항을 지닌 convex한 목적함수를 최적화하는 $B$를 찾기 위해 라그랑주 승수법을 적용한다. 라그랑주 승수법은 어떠한 제약 조건 하에서 다변수 함수의 극대, 극소 등 임계점을 구하기 위해 사용하는 방법이다.
제약사항인 $\text{diag}(B) - 0$에 $\gamma$를 곱한 항을 목적함수와 더해서 Lagrangian이라고 불리는 함수 $L$을 정의한다.
위에서 $\gamma^\intercal \cdot \text{diag}(B)$에 2를 곱한 이유는 식의 정리를 편하게 하기 위해 의도하여 곱한 값이다.
결국 $L$을 최소화하는 해인 $\hat{B}$를 찾아야 하는데, 이는 $L$의 도함수를 0으로 만드는 $B$를 찾으면 된다. 그래서 우변을 $B$로 미분했을 때 0이 되게 하는 $B$를 정리하여 구하면 다음과 같다.
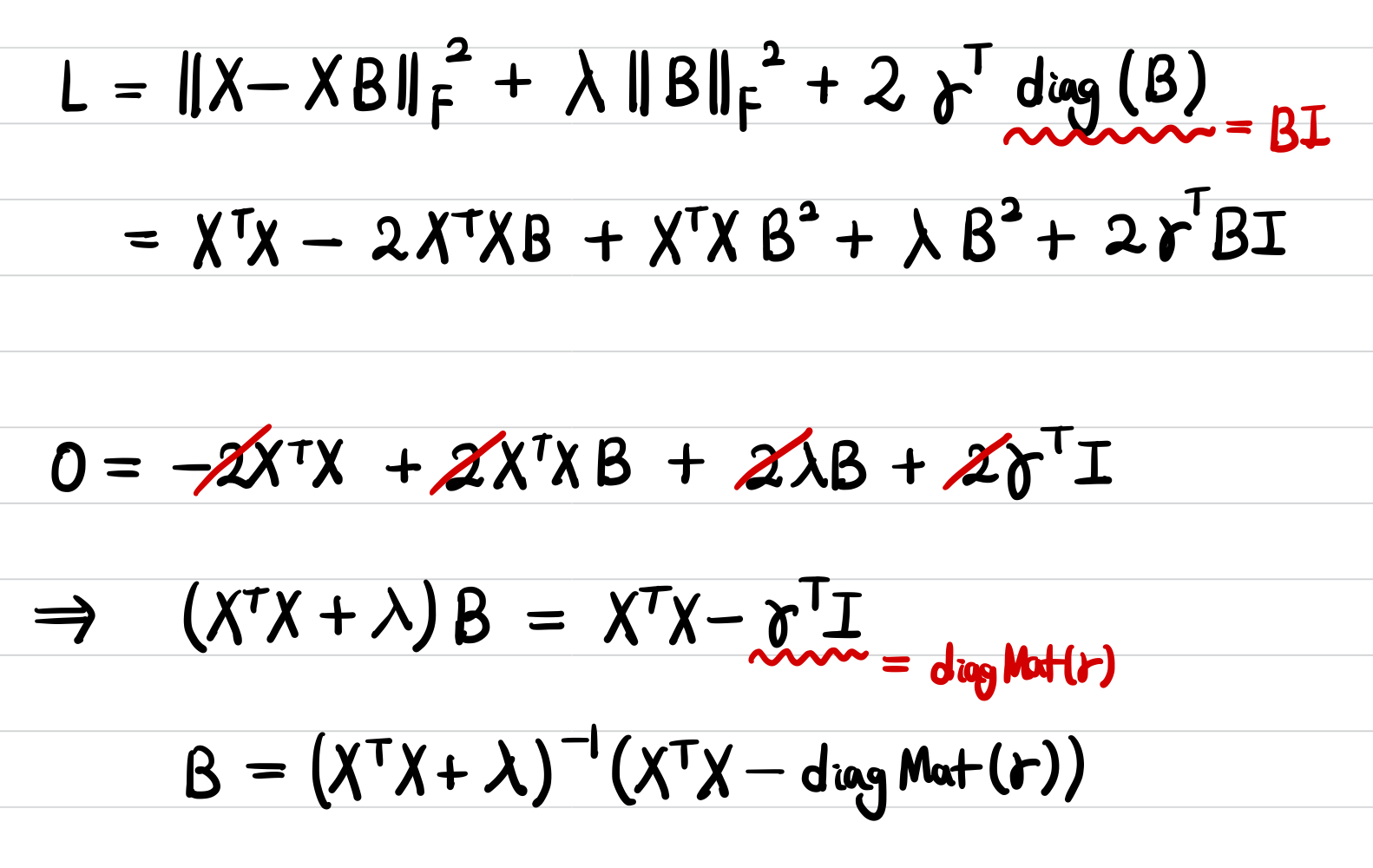
[행렬의 Norm의 제곱을 구하는 데 참고한 페이지]
Squared norm of matrix equal to squared norm of its transpose
With the definition of matrix norm as $$\|M \|=\sup_x \{ |Mx|: |x|=1 \},$$ where $M$ is square and $|\cdot|$ denotes the standard euclidean 2-norm. I'm trying to prove that $$\|M\|^2=\|M^T\|^...
math.stackexchange.com
[행렬의 Frobenius Norm 미분하는 방법]
https://math.stackexchange.com/questions/2128462/derivative-of-squared-frobenius-norm-of-a-matrix
Derivative of squared Frobenius norm of a matrix
In linear regression, the loss function is expressed as $$\frac1N \left\|XW-Y\right\|_{\text{F}}^2$$ where $X, W, Y$ are matrices. Taking derivative w.r.t $W$ yields $$\frac 2N \, X^T(XW-Y)$$ ...
math.stackexchange.com
이제 위의 식을 좀 더 깔끔하게 정리하기 위해 충분히 큰 $\lambda$에 관하여 $\hat{P}$를 새로 정의한다.
$\hat{P}$를 치환하여 식을 다시 정리하면 다음과 같다.
위의 마지막 줄에서 $\tilde{γ} ≜ λ\vec{1}+γ$로 정의되며, 라그랑주 승수인 $\tilde{γ}$의 값은 $\text{diag}(\hat{B})=0$이라는 제약사항에 의해서 결정될 수 있다.
여기서 $\odot$은 elementwise product이고, 이를 $\tilde{\gamma}$에 관해 elementwise division으로 또 정리하면 다음과 같다.
이를 다시 $\hat{B}$에 치환하여 정리하면 다음과 같이 정리된다.
학습되는 파라미터의 가중치인 $\hat{B}$의 각 원소 값을 정리하면 다음과 같다.
만약에 앞에서 $B$의 대각성분을 0으로 제한하지 않았으면 이러한 해가 도출되지 못했을 것이다.
대각성분이 아닌 원소들은 모두 $\hat{P}$에 의해 결정되는데, 이는 앞에서 정의한 식 $\hat{P} = (X^TX+λI)^{−1}$를 따른다.
$\hat{P}$는 반드시 대칭 행렬이지만 일반적으로 $\hat{B}$는 비대칭 행렬일 수 있는데, 이는 식을 보면 이해할 수 있다. 단순하게 $i=3$이면서 $j=4$일 때, $i=4$이면서 $j=3$일 때를 생각해보면 결국 $\hat{P}$가 대칭 행렬이어도 $-\frac{\hat{P}_{ij}}{\hat{P}_{jj}}$의 분모에 의해 값이 달라질 수 있다는 것을 눈치챌 수 있다.
$\lambda$는 이미 하이퍼파라미터로 주어지므로 결국 $\hat{P}$를 추정하기 위해서는 $G = X^TX$이 중요해진다.
결국 입력 데이터에 의해 $B$에 영향을 주는 건 바로 이 $X^TX$인 것이다.
이 $X^TX$는 item-to-item matrix이고, $X^TX$와 같은 꼴을 Gram-matrix라고 한다.
논문에서는 이 Gram-matrix가 co-occurrence matrix라고 말하는데, 이 co-occurrence matrix가 뭔지 싶어서 여러 군데를 찾아봤더니 NLP에서 주로 사용하는 개념이었다.
[NLP에서의 co-occurrence matrix]
자연어처리(NLP) 15일차 (GloVe)
2019.06.18
omicro03.medium.com
NLP에서는 어떤 한 단어와 함께 특정 단어가 몇 번 등장했는지를 나타내는 행렬로 정의하는데, 이 논문에서도 비슷하게 적용해볼 수 있다.
이 논문에서는 $X^TX$를 어떤 한 아이템이 유저에게 선택되었을 때, 다른 아이템도 같이 선택되었을 빈도가 어느 정도인지를 나타내는 행렬로 이해해볼 수 있다.
앞에서 들었던 예시를 다시 가져와서 적용해보면 좀 더 의미가 와닿을 것이다.
| 아이템 a | 아이템 b | 아이템 c | 아이템 d | |
|---|---|---|---|---|
| 유저 A | 0 | 1 | 1 | 0 |
| 유저 B | 1 | 0 | 1 | 1 |
| 유저 C | 0 | 0 | 0 | 1 |
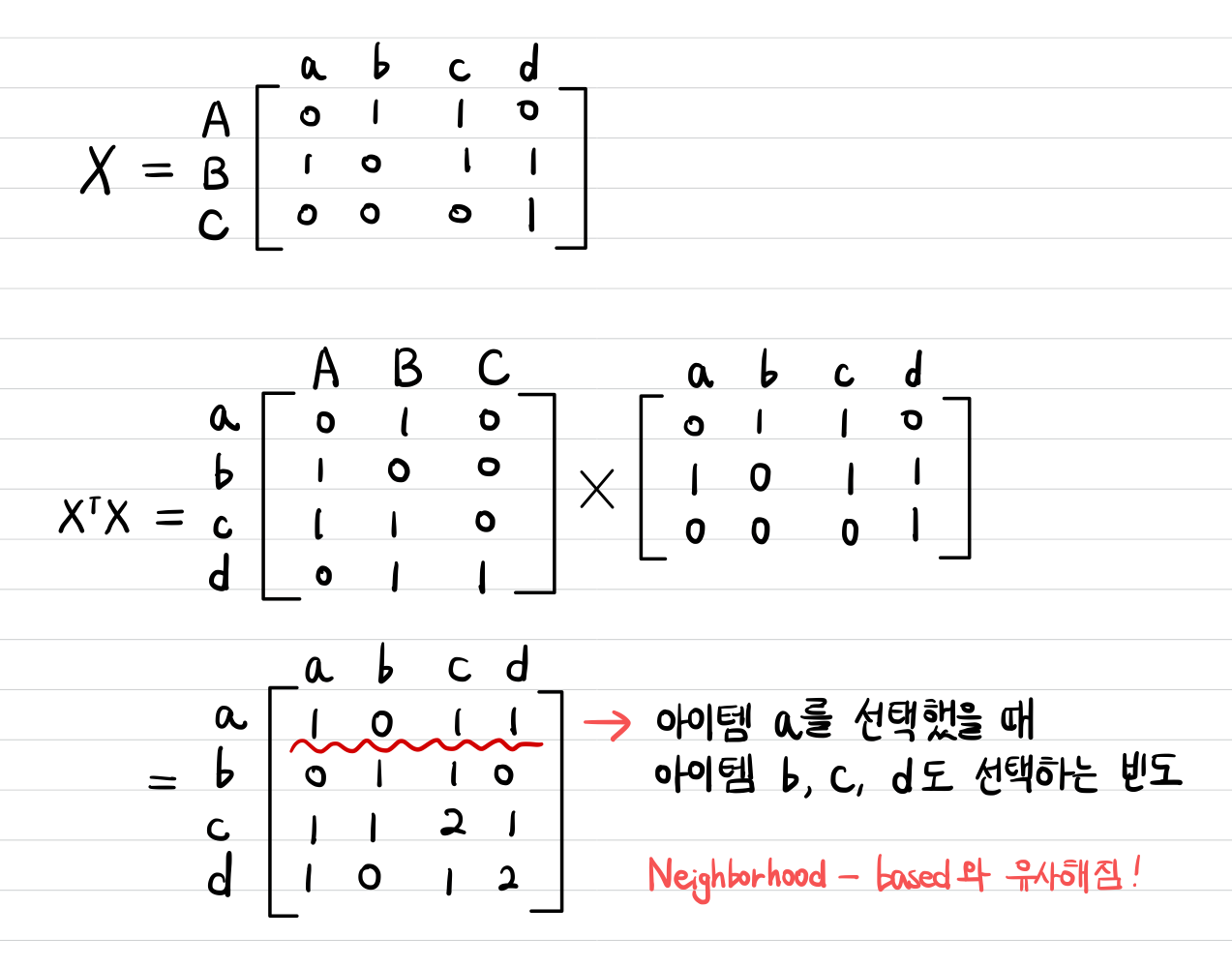
결국 co-occurrence matrix를 구하는 것이 아이템 간의 유사도를 구하는 Neighborhood-based Collaborative Filtering과 매우 유사함을 알 수 있는데, 논문에서도 기존의 Neighborhood-based 접근법의 한계를 지적하면서 EASE에서의 장점을 더 강조하고 있다. 이는 아래에서 소개할 것이다.
이 co-occurrence 계수인 $G_{ij}$의 불확실성은 대략 Poisson distribution(푸아송 분포)의 표준편차인 $\sqrt{G_{ij}}$에 의해 결정된다고 한다.
또한 이 co-occurrence의 계수가 충분히 크면 $G$와 $B$는 작은 에러로 추정할 수 있다고 서술되어 있다. 사실 이 부분이 이해가 가지 않아서 잘 와닿지 않았는데, G의 값이 커지면 regularization term의 영향력이 작아져서 그런 건가 하는 추측을 했다. 이에 관해 자세히 알아보고 내용을 보충해야겠다.
Gram matrix와 EASE의 관계
흥미롭게도 $G = X^TX$의 entry가 두 가지 다른 요인에 의해 증가될 수 있다고 하는데, 개인적으로 이 부분이 EASE의 핵심이 아닐까 하는 생각이 들었다.
- 활동량이 증가한 유저로 인해 더 밀도가 높아진 데이터 $X$에 의해서 $G$의 entry가 커질 수 있다.
- $X$의 유저 수가 증가함으로 인하여 $G$의 entry가 커질 수 있다.
두 번째 요인에 주목해야 하는데, 이는 유저의 수가 증가하면 데이터의 sparsity가 어느 정도 보완될 수 있음을 시사하고 있다.
그래서 데이터에서 유저의 수가 충분히 크면 $G$의 entry 값이 커져서 학습 파라미터인 $B$를 작은 에러로 추정하여 불확실성을 줄일 수 있고, 이는 결국 데이터에서 유저마다 활동량이 많지 않은 sparse함이 $B$를 추정하는 데 큰 영향을 끼치지 않는다는 점을 유추할 수 있다.
이것이 결론적으로 EASE가 왜 sparse한 데이터에 robust한 모델인지를 알려주는 핵심이라고 생각된다.
아이템이 유저보다 적으면 적을수록 연산 효율 증가
위처럼 목적함수를 최적화 하는 해를 구하는 것이 closed form solution이어서 굳이 딥 러닝을 사용할 필요 없이 단순 CPU로도 충분하여 컴퓨팅 자원이 적게 든다.
또한 파라미터를 업데이트하기 위해 결과적으로 유저와 아이템의 interaction 행렬인 $X$ 그 자체가 아니라 $G = X^TX$를 사용한다. 이때 $X$의 크기는 $|U| \times |I|$인 반면에 $G$의 크기는 $|I| \times |I|$이어서 아이템의 수가 유저의 수보다 상대적으로 작으면 알고리즘의 연산 효율성이 증가한다. 반대로 아이템의 수가 유저의 수보다 상대적으로 많으면 연산 효율성이 떨어진다. 이번에 참여한 대회에서도 유저의 수가 31,360명인데 반해 아이템의 수는 6807개였는데, 이처럼 아이템의 수가 유저 수보다 작았던 것이 더 빠른 시간 내로 연산을 가능하게 했던 게 아닐까 하는 생각이 들었다.
학습 과정 구현
위의 내용을 종합하여 EASE 모델의 학습 과정을 코드로 구현하면 다음과 같다.
import numpy as np
# 딥 러닝 모델이 아니므로 nn.Module을 상속받을 필요가 없다.
class EASE:
def __init__(self, _lambda):
self.B = None
self._lambda = _lambda
def train(self, X):
G = X.T @ X # G = X'X
diag_indices = list(range(G.shape[0]))
G[diag_indices, diag_indices] += self._lambda # X'X + λI
P = np.linalg.inv(G) # P = (X'X + λI)^(-1)
self.B = P / -np.diag(P) # - P_{ij} / P_{jj} if i ≠ j
min_dim = min(*self.B.shape)
self.B[range(min_dim), range(min_dim)] = 0 # 대각행렬 원소만 0으로 만들어주기 위해
def forward(self, user_row):
return user_row @ self.B
입력 데이터에 관한 학습 과정은 매우 간단하다.
X = inputs # 학습 데이터
_lambda = 300
ease = EASE(_lambda)
ease.train(X)
이제 입력 데이터 $X$에서 각 유저별로 활동 이력이 없는 아이템 중 어떠한 아이템을 보여주는 것이 좋은지 ranking을 구하는 inference 과정은 다음과 같이 할 수 있다.
result = ease.forward(X[:, :])
result[X.nonzero()] = -np.inf # 이미 어떤 한 유저가 클릭 또는 구매한 아이템 이력은 제외
주의할 점은 우리는 $X$에서 각 유저별로 feedback이 0인 아이템 중에서 유저가 원할 것 같은 아이템을 추천해야 하므로 이미 유저가 클릭 또는 구매한 아이템 원소 값은 제외해야 한다.
EASE와 다른 모델 간의 비교
Neighborhood-based CF 방법과의 비교
The closed form solution reveals that the inverse of the data Gram matrix is the conceptually correct similarity matrix.
위에서 구한 과정에서 $\lambda I$는 제외하고 살펴보면 EASE에서도 neighborhood-based 접근법과 유사하게 $G = X^TX$라는 co-occurrence matrix이자 Gram-matrix를 사용한다. 그런데 EASE에서는 $G = X^TX$를 그대로 학습 파라미터 $B$에 반영하는 것이 아니라 $G$를 inverse한 행렬인 $\hat{P}$를 사용한다. 그래서 기존의 neighborhood-based 모델에서 Gram-matrix $G$를 그대로 유사도 행렬로 사용하는 것은 개념적으로 틀리다고 지적하고 있다. EASE처럼 $G$의 역행렬을 유사도 행렬로서 사용하는 것이 개념적으로 맞음을 강조하고 있다.
EASE에 관하여 아직 더 정리해야 할 부분이 남아 있는데, 이는 추후에 계속 업데이트하여 완성할 예정이다.
EASE에 관하여 느낀 점
실제로 EASE 모델을 사용하면서 들었던 의문점이 있었는데, 우선 간략히 정리하고 추후에 글을 더 업데이트할 때 자세히 기록을 남길 예정이다.
- EASE의 입력 데이터에서 Positive feedback 값으로서 1이 아닌 0.9로 설정했더니 약간의 성능 향상을 경험할 수 있었다. 그런데 1보다 더 큰 값을 주면 오히려 성능이 낮아지는 것을 목격했다. 아마 positive feedback value가 $G$의 계수의 불확실성인 포아송 분포의 표준편차에 영향을 끼치는 것이 아닌가 하는 생각이 들었다. 그런데 논문에서 $G$의 계수가 늘어나면 분명 $G$와 $B$를 추정하는 에러가 줄어든다고 한 것 같은데 그러면 성능이 더 좋아져야 하는 게 아닌가 하는 생각이 들었다. 사실 대회에서는 EASE를 단독으로 사용하지 않고 minmaxscaler를 적용한 후 다른 모델과 앙상블하는 방식을 사용해서 점수가 높아진 건 단순 우연일 수도 있다. 그렇지만 좀 더 깊이 있게 공부해서 이에 관한 해답을 탐구해 보고 싶다.
- $\lambda$를 어느 정도의 값으로 주는 것이 가장 바람직한지에 관해 의문이 들었다. 실제로 실습한 코드에서는 이 값을 300으로 설정했을 때가 가장 성능이 좋았는데, 항상 정규화 항을 사용하여 과적합과 과소적합을 조절하는 것이 까다로움을 느꼈다.
- EASE를 이번 대회에서 사용했을 때 다른 모델에 비해 성능이 좋게 나왔던 것은 아무래도 대회에서 사용한 데이터가 sequential data가 아니라 중간 중간 빈 부분이 뚫려 있는 좀 더 sparse한 데이터에 가까워 cold start problem이 발생해서인 것으로 보인다.
코드 구현
RECJOON 프로젝트를 진행하면서 BOJ(백준 온라인 저지) 유저와 문제풀이 dataset을 가지고 EASE 모델을 통해 학습하고 inference을 수행하는 과정을 jupyter notebook으로 작성한 코드이다.
GitHub - Glanceyes/ML-Paper-Review: Implementation of ML&DL models in machine learning that I have studied and written source co
Implementation of ML&DL models in machine learning that I have studied and written source code myself - GitHub - Glanceyes/ML-Paper-Review: Implementation of ML&DL models in machine learnin...
github.com
출처
1. https://arxiv.org/abs/1905.03375
2. https://www.devchopin.com/blog/364
3. https://velog.io/@chwchong/Embarrassingly-Shallow-Autoencoders-for-Sparse-Data-ad26xu1w
4. https://xiaobaiha.gitbook.io/tech-share/machinelearning/embarassingly-autoencoder-suan-fa
5. https://www.kaggle.com/code/lucamoroni/ease-implementation
'AI > 추천 시스템' 카테고리의 다른 글
| Deep Learning 기반의 Collaborative Filtering (0) | 2022.04.18 |
|---|---|
| 추천 시스템에서의 Implicit Feedback (0) | 2022.04.18 |
| Memory-based와 Model-based Collaborative Filtering (0) | 2022.04.02 |
| Top-K Ranking 문제에서 추천시스템을 평가하는 지표 (0) | 2022.03.27 |
| 추천 시스템의 핵심이 되는 여러 방법론 (0) | 2022.03.27 |
소중한 공감 감사합니다.